hrbustoj 1429:凸多边形（计算几何，判断点是否在多边形内，二分法）

凸多边形

Time Limit: 2000 MS    Memory Limit: 65536 K

Total Submit: 130(24 users)   Total Accepted: 40(18 users)       Rating:         Special Judge: No

Description

已知一个凸多边形A（包含n个点，点按照顺时针给出），和一个点集B（包含m个点），请判断这m个点是否都严格在凸多边形A内部。

 

Input

输入包含多组测试数据。

对于每组测试数据：

第1行，包含一个整数n (3 ≤ n ≤ 105)代表着凸多边形A的点的数量。

接下来n行每行包含一个坐标(x, y) (-109 ≤ x, y ≤ 109) 表示这个凸多边形，点按照顺时针给出。

第n + 2行，包含一个整数m (3 ≤ m ≤ 105)代表着点集B的点的数量。

接下来m行每行包含一个坐标(x, y) (-109 ≤ x, y ≤ 109) 表示这个点集B。

处理到文件结束

 

Output

对于每组测试数据：

第1行，如果点集B都严格在凸多边形A内，输出YES，否则输出NO。

 

Sample Input

4

-10 -10

-10 10

10 10

10 -10

3

0 0

1 1

2 2

4

-10 -10

-10 10

10 10

10 -10

3

100 100

1 1

2 2

 

Sample Output

YES

NO

 

Author

齐达拉图@HRBUST

---

 

　　计算几何，判断点是否在多边形内（二分法）。

　　判断点是否在多边形内有多种方法，例如：射线法，角度和判断法，弧长法，二分法。

　　射线法是我最开始学的方法，较麻烦；角度和判断法也叫转角法，比较方便，但是由于要计算大量的反三角函数，所以速度较慢，容易产生精度误差。而弧长法的优点恰恰就是精度高，只需作乘法和减法，若对整数坐标则完全没有精度问题。而且实现简单，比射线法和转角法都好写。二分法速度最快，特别适应于判断多个点是否在多边形内的情况。就像这道题。

　　其中前三种方法时间复杂度都是O(n)，二分法时间复杂度是O(logn)。

　　这道题的题意是已知构成凸多边形A的n个点的坐标，和点集B的m个点的坐标，求这B的m个点是否都在凸多边形A内（严格内部，就是点不能在多边形边上）。

　　思路：用以上前三种方法的任意一种都会超时，时间复杂度为(O(mn))，遂使用二分法，这道题的时间复杂度为(O(mlogn))。

　　二分法求多边形的步骤：

　　1、选择多边形其中一个点为起点，连接其它点作射线。

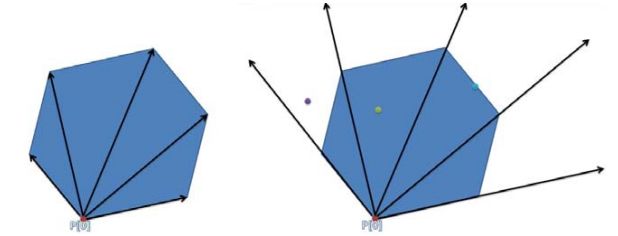
　　2、判断给定的点是否在所有射线包围的区域之内，即判断给定点是否在最左侧射线的左边，或者在最右侧射线的右边。

　　3、如果在射线包围的区域之内，选择构成最两侧的射线的点为left和right，则mid = (left+right)/2，连接给顶点和起点作射线，判断该射线在mid点和起点的哪一边，不断循环，如此用二分法最后求出给定点所在的三角形区域，由此确定了除起点外的一条边。

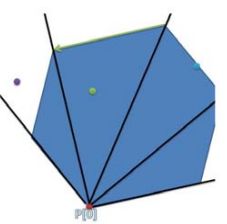
　　4、判断给定点在这条边的左方还是右方，由此判断给定点是否在三角形区域内，也就是是否在多边形内。

　　注意：这道题有个坑，点要求严格在多边形内部，也就是说不能在多边形的边上。注意这一点，测试数据控制的很严格，WA了好多次才明白过来。

　　代码：

 1 #include <stdio.h>

 2 #define eps 1e-10

 3 struct Point{  4     double x,y;  5 };  6 double xmulti(Point p1,Point p2,Point p0)    //求p1p0和p2p0的叉积,如果大于0,则p1在p2的顺时针方向

 7 {  8     return (p1.x-p0.x)*(p2.y-p0.y)-(p2.x-p0.x)*(p1.y-p0.y);  9 } 10 Point A[100001],B[100001]; 11 int main() 12 { 13     int i,n,m; 14     while(scanf("%d",&n)!=EOF){ 15         for(i=1;i<=n;i++)    //输入多边形的顶点

16             scanf("%lf%lf",&A[i].x,&A[i].y); 17         scanf("%d",&m); 18         for(i=1;i<=m;i++)    //输入点集

19             scanf("%lf%lf",&B[i].x,&B[i].y); 20         //二分法判断B上的点是否在原凸多边形A内，注意在边上不行

21         for(i=1;i<=m;i++){    //B[i]

22             if(xmulti(B[i],A[2],A[1])<=eps || xmulti(B[i],A[n],A[1])>=-eps)    //在第一个点为起点的扇形之外或在边上

23                 break; 24             int left=2,right=n; 25             while(right-left!=1){ 26                 int mid = (left+right)/2; 27                 if(xmulti(B[i],A[mid],A[1])>eps) 28                     left = mid; 29                 else 

30                     right = mid; 31  } 32             if(xmulti(B[i],A[right],A[left])<=eps)    //在边之外或在边上

33                 break; 34  } 35         if(i>m) 36             printf("YES\n"); 37         else

38             printf("NO\n"); 39  } 40     return 0; 41 }

 

Freecode : www.cnblogs.com/yym2013