计算物理精解【3】
文章目录
- 力学
-
- 单位矢量
-
- 基础
- 定义
- 矢量加法
-
- 矢量加法的几何方法
- 矢量加法的代数方法
- 示例
- 注意事项
- 矢量间的关系
- 矢量(或向量)的标量积(也称为点积、内积或数量积)性质
- 计算两矢量之间的夹角
-
- 例子
- 步骤
- 数值结果
- 计算两三维矢量之间夹角的例子
-
- 例子
- 步骤
- 数值结果
- 通过单位矢量计算标量积
- 矢量(向量)的向量积(也称为叉积、外积或叉乘)
-
- 性质
- 如何计算矢量向量积
- 示例
- 例子
- 步骤
- 最终结果
- 注意
- 单位矢量
-
- 性质
- 示例
- 应用
- 矢量的位移
-
- 定义
- 计算公式
- 性质
- 应用
- 示例
- 参考文献
力学
单位矢量
也称为单位向量,是模(或长度)等于1的矢量。在物理学、数学和工程学中,单位矢量经常用于表示方向,因为它们的大小是固定的,只包含方向信息。
基础
- 大小精确为1,指向某一特定方向的矢量称为单位矢量
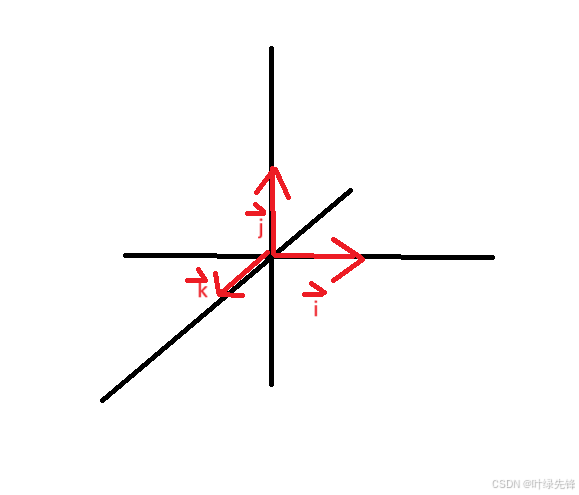
- 用单位矢量表示其它矢量。 比如 a ⃗ 的矢量分量可表示为 a x i ⃗ + b y j ⃗ 用单位矢量表示其它矢量。\\比如\vec a的矢量分量可表示为a_x\vec i+b_y\vec j 用单位矢量表示其它矢量。比如a的矢量分量可表示为axi+byj
定义
对于任意非零矢量 A ⃗ \vec{A} A,其单位矢量 A ^ \hat{A} A^定义为:
A ^ = A ⃗ ∣ A ⃗ ∣ \hat{A} = \frac{\vec{A}}{|\vec{A}|} A^=∣A∣A
其中, ∣ A ⃗ ∣ |\vec{A}| ∣A∣是矢量 A ⃗ \vec{A} A的模(或长度)。
- 如果两个矢量的分量相同,则两矢量相同。
矢量加法
是数学和物理学中的一个基本概念,它描述了如何对两个或多个矢量进行相加。矢量是既有大小(模)又有方向的量,通常用带有箭头的线段来表示。在二维或三维空间中,我们可以使用坐标系统来描述矢量的位置和大小。
矢量加法的几何方法
在几何上,矢量加法可以通过“平行四边形法则”或“三角形法则”来实现。
- 平行四边形法则:将两个矢量作为平行四边形的相邻两边,则这两个矢量的和就是平行四边形的对角线。
- 三角形法则:将两个矢量首尾相接,从第一个矢量的起点到第二个矢量的终点的有向线段就是这两个矢量的和。
矢量加法的代数方法
在代数上,如果我们在二维空间中,有两个矢量 A ⃗ = ( A x , A y ) \vec{A} = (A_x, A_y) A=(Ax,Ay) 和 B ⃗ = ( B x , B y ) \vec{B} = (B_x, B_y) B=(Bx,By),则它们的和 C ⃗ = A ⃗ + B ⃗ \vec{C} = \vec{A} + \vec{B} C=A+B 可以通过坐标相加得到:
C ⃗ = ( A x + B x , A y + B y ) \vec{C} = (A_x + B_x, A_y + B_y) C=(Ax+Bx,Ay+By)
同样地,在三维空间中,如果有三个分量,则:
C ⃗ = ( A x + B x , A y + B y , A z + B z ) \vec{C} = (A_x + B_x, A_y + B_y, A_z + B_z) C=(Ax+Bx,Ay+By,Az+Bz)
示例
假设有两个二维矢量 A ⃗ = ( 2 , 3 ) \vec{A} = (2, 3) A=(2,3) 和 B ⃗ = ( 4 , − 1 ) \vec{B} = (4, -1) B=(4,−1),我们需要找到它们的和 C ⃗ \vec{C} C。
使用代数方法:
C ⃗ = A ⃗ + B ⃗ = ( 2 + 4 , 3 + ( − 1 ) ) = ( 6 , 2 ) \vec{C} = \vec{A} + \vec{B} = (2 + 4, 3 + (-1)) = (6, 2) C=A+B=(2+4,3+(−1))=(6,2)
所以, C ⃗ = ( 6 , 2 ) \vec{C} = (6, 2) C=(6,2)。
注意事项
- 矢量加法满足交换律和结合律,即 A ⃗ + B ⃗ = B ⃗ + A ⃗ \vec{A} + \vec{B} = \vec{B} + \vec{A} A+B=B+A 和 ( A ⃗ + B ⃗ ) + C ⃗ = A ⃗ + ( B ⃗ + C ⃗ ) (\vec{A} + \vec{B}) + \vec{C} = \vec{A} + (\vec{B} + \vec{C}) (A+B)+C=A+(B+C)。
- 矢量加法的结果仍然是一个矢量,它的大小和方向由参与加法的矢量共同决定。
- 矢量与标量的乘法(即数乘)是另一种运算,它改变矢量的大小但不改变其方向(除非标量为负,此时方向反转)。
矢量间的关系
主要涉及到矢量之间的加法、减法、数乘(即标量与矢量的乘法)、点积(内积、标量积)、叉积(外积、向量积,主要在三维空间中定义)以及它们之间的夹角、平行、垂直等概念。以下是对这些关系的一些简要说明:
-
加法与减法:
- 矢量加法:如上所述,通过平行四边形法则或三角形法则进行。
- 矢量减法:可以看作是加上一个与减数大小相等但方向相反的矢量。即 A ⃗ − B ⃗ = A ⃗ + ( − B ⃗ ) \vec{A} - \vec{B} = \vec{A} + (-\vec{B}) A−B=A+(−B)。
-
数乘:
- 标量与矢量的乘法:结果是一个矢量,其大小是原矢量大小的标量倍,方向与原矢量相同(标量为正)或相反(标量为负)。
-
点积(内积、标量积):
- 定义:两个矢量 A ⃗ \vec{A} A 和 B ⃗ \vec{B} B 的点积是一个标量,表示为 A ⃗ ⋅ B ⃗ \vec{A} \cdot \vec{B} A⋅B 或 A ⋅ B A \cdot B A⋅B。
- 计算公式(二维): A ⃗ ⋅ B ⃗ = A x B x + A y B y \vec{A} \cdot \vec{B} = A_x B_x + A_y B_y A⋅B=AxBx+AyBy。
- 计算公式(三维): A ⃗ ⋅ B ⃗ = A x B x + A y B y + A z B z \vec{A} \cdot \vec{B} = A_x B_x + A_y B_y + A_z B_z A⋅B=AxBx+AyBy+AzBz。
- 性质:点积满足交换律、分配律,但不满足结合律(因为结合律要求所有元素都是矢量或标量,而点积的结果是标量)。
- 应用:计算两矢量之间的夹角、判断两矢量的垂直关系(如果 A ⃗ ⋅ B ⃗ = 0 \vec{A} \cdot \vec{B} = 0 A⋅B=0,则 A ⃗ \vec{A} A 垂直于 B ⃗ \vec{B} B)。
- 也可以如下方式计算:
A ⃗ ⋅ B ⃗ = ∣ A ∣ ∣ B ∣ c o s α \vec{A} \cdot \vec{B} =|A||B|cos\alpha A⋅B=∣A∣∣B∣cosα
-
叉积(外积、向量积,三维空间特有):
- 定义:两个三维矢量 A ⃗ \vec{A} A 和 B ⃗ \vec{B} B 的叉积是一个矢量,表示为 A ⃗ × B ⃗ \vec{A} \times \vec{B} A×B。
- 计算公式: A ⃗ × B ⃗ = ( A y B z − A z B y , A z B x − A x B z , A x B y − A y B x ) \vec{A} \times \vec{B} = (A_y B_z - A_z B_y, A_z B_x - A_x B_z, A_x B_y - A_y B_x) A×B=(AyBz−AzBy,AzBx−AxBz,AxBy−AyBx)。
- 性质:叉积不满足交换律( A ⃗ × B ⃗ = − B ⃗ × A ⃗ \vec{A} \times \vec{B} = -\vec{B} \times \vec{A} A×B=−B×A),满足分配律。
- 应用:计算两矢量的垂直分量、判断两矢量的平行或垂直关系(如果 A ⃗ × B ⃗ = 0 ⃗ \vec{A} \times \vec{B} = \vec{0} A×B=0,则 A ⃗ \vec{A} A 平行于 B ⃗ \vec{B} B 或两矢量中至少有一个是零矢量)。
-
夹角:
- 通过点积可以计算两个非零矢量之间的夹角 θ \theta θ,公式为 cos θ = A ⃗ ⋅ B ⃗ ∣ A ⃗ ∣ ⋅ ∣ B ⃗ ∣ \cos\theta = \frac{\vec{A} \cdot \vec{B}}{|\vec{A}| \cdot |\vec{B}|} cosθ=∣A∣⋅∣B∣A⋅B。
-
平行与垂直:
- 如果两个矢量共线(即方向相同或相反),则称它们平行。
- 如果两个矢量的点积为零(在二维或三维空间中),则称它们垂直。
这些关系在物理学、工程学、计算机科学等领域中都有广泛的应用。
矢量(或向量)的标量积(也称为点积、内积或数量积)性质
是线性代数中的一个重要概念,它涉及到两个矢量的运算,并返回一个标量(即一个实数)。设有两个矢量 a \mathbf{a} a 和 b \mathbf{b} b,它们的标量积通常表示为 a ⋅ b \mathbf{a} \cdot \mathbf{b} a⋅b 或 ⟨ a , b ⟩ \langle \mathbf{a}, \mathbf{b} \rangle ⟨a,b⟩。以下是矢量标量积的一些主要性质:
-
交换律:
a ⋅ b = b ⋅ a \mathbf{a} \cdot \mathbf{b} = \mathbf{b} \cdot \mathbf{a} a⋅b=b⋅a
即,两个矢量的标量积与它们的顺序无关。 -
分配律:
a ⋅ ( b + c ) = a ⋅ b + a ⋅ c \mathbf{a} \cdot (\mathbf{b} + \mathbf{c}) = \mathbf{a} \cdot \mathbf{b} + \mathbf{a} \cdot \mathbf{c} a⋅(b+c)=a⋅b+a⋅c
即,标量积满足对加法的分配律。 -
与标量的乘法:
( k a ) ⋅ b = k ( a ⋅ b ) = a ⋅ ( k b ) (k\mathbf{a}) \cdot \mathbf{b} = k(\mathbf{a} \cdot \mathbf{b}) = \mathbf{a} \cdot (k\mathbf{b}) (ka)⋅b=k(a⋅b)=a⋅(kb)
其中 k k k 是任意标量。即,标量可以“穿过”标量积。 -
零矢量:
a ⋅ 0 = 0 \mathbf{a} \cdot \mathbf{0} = 0 a⋅0=0
其中 0 \mathbf{0} 0 是零矢量。即,任何矢量与零矢量的标量积都是零。 -
模与夹角的关系:
a ⋅ b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ cos θ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| \cdot |\mathbf{b}| \cdot \cos \theta a⋅b=∣a∣⋅∣b∣⋅cosθ
其中 ∣ a ∣ |\mathbf{a}| ∣a∣ 和 ∣ b ∣ |\mathbf{b}| ∣b∣ 分别是 a \mathbf{a} a 和 b \mathbf{b} b 的模(长度), θ \theta θ 是 a \mathbf{a} a 和 b \mathbf{b} b 之间的夹角( 0 ≤ θ ≤ π 0 \leq \theta \leq \pi 0≤θ≤π)。这个公式揭示了标量积与矢量模长及它们之间夹角的关系。 -
正交性:
如果 a ⋅ b = 0 \mathbf{a} \cdot \mathbf{b} = 0 a⋅b=0,则称 a \mathbf{a} a 和 b \mathbf{b} b 是正交的(或垂直的)。在二维和三维空间中,这通常意味着两个矢量在直角坐标系中形成的角度是 9 0 ∘ 90^\circ 90∘。 -
自乘:
a ⋅ a = ∣ a ∣ 2 \mathbf{a} \cdot \mathbf{a} = |\mathbf{a}|^2 a⋅a=∣a∣2
即,一个矢量与其自身的标量积等于该矢量模长的平方。
这些性质使得标量积在物理和工程领域中有广泛的应用,例如在力学中计算功、在电磁学中计算电场力等。
计算两矢量之间的夹角
是线性代数中的一个常见问题,特别是在物理学和工程学中。这里,我将给出一个具体的例子和步骤来计算两个矢量之间的夹角。
例子
假设有两个二维矢量 a = ( 2 , 3 ) \mathbf{a} = (2, 3) a=(2,3) 和 b = ( 4 , − 1 ) \mathbf{b} = (4, -1) b=(4,−1),我们需要计算这两个矢量之间的夹角 θ \theta θ。
步骤
-
计算两个矢量的模长:
- 矢量 a \mathbf{a} a 的模长 ∣ a ∣ |\mathbf{a}| ∣a∣ 可以通过 2 2 + 3 2 = 4 + 9 = 13 \sqrt{2^2 + 3^2} = \sqrt{4 + 9} = \sqrt{13} 22+32=4+9=13 计算得到。
- 矢量 b \mathbf{b} b 的模长 ∣ b ∣ |\mathbf{b}| ∣b∣ 可以通过 4 2 + ( − 1 ) 2 = 16 + 1 = 17 \sqrt{4^2 + (-1)^2} = \sqrt{16 + 1} = \sqrt{17} 42+(−1)2=16+1=17 计算得到。
-
计算两个矢量的标量积:
- 矢量 a \mathbf{a} a 和 b \mathbf{b} b 的标量积 a ⋅ b \mathbf{a} \cdot \mathbf{b} a⋅b 可以通过 2 × 4 + 3 × ( − 1 ) = 8 − 3 = 5 2 \times 4 + 3 \times (-1) = 8 - 3 = 5 2×4+3×(−1)=8−3=5 计算得到。
-
使用标量积和模长来计算夹角:
- 根据标量积的定义,我们有 a ⋅ b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ cos θ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| \cdot |\mathbf{b}| \cdot \cos \theta a⋅b=∣a∣⋅∣b∣⋅cosθ。
- 将已知的 ∣ a ∣ |\mathbf{a}| ∣a∣、 ∣ b ∣ |\mathbf{b}| ∣b∣ 和 a ⋅ b \mathbf{a} \cdot \mathbf{b} a⋅b 代入上式,得到 5 = 13 ⋅ 17 ⋅ cos θ 5 = \sqrt{13} \cdot \sqrt{17} \cdot \cos \theta 5=13⋅17⋅cosθ。
- 解这个方程以求出 cos θ \cos \theta cosθ,即 cos θ = 5 13 ⋅ 17 \cos \theta = \frac{5}{\sqrt{13} \cdot \sqrt{17}} cosθ=13⋅175。
- 最后,使用反余弦函数 arccos \arccos arccos 来求出 θ \theta θ,即 θ = arccos ( 5 13 ⋅ 17 ) \theta = \arccos\left(\frac{5}{\sqrt{13} \cdot \sqrt{17}}\right) θ=arccos(13⋅175)。
- 注意,由于 arccos \arccos arccos 的值域是 [ 0 , π ] [0, \pi] [0,π],所以得到的 θ \theta θ 是两个矢量之间的最小夹角(以弧度为单位)。如果需要以度为单位,可以使用转换公式 θ deg = θ rad × 180 π \theta_{\text{deg}} = \theta_{\text{rad}} \times \frac{180}{\pi} θdeg=θrad×π180。
数值结果
由于这里涉及到无理数的运算,我们通常会使用计算器或编程软件来得到数值结果。经过计算,我们得到 θ ≈ 0.6458 \theta \approx 0.6458 θ≈0.6458 弧度,转换为度则是 θ ≈ 0.6458 × 180 π ≈ 37.1 3 ∘ \theta \approx 0.6458 \times \frac{180}{\pi} \approx 37.13^\circ θ≈0.6458×π180≈37.13∘。
因此,矢量 a = ( 2 , 3 ) \mathbf{a} = (2, 3) a=(2,3) 和 b = ( 4 , − 1 ) \mathbf{b} = (4, -1) b=(4,−1) 之间的夹角约为 37.1 3 ∘ 37.13^\circ 37.13∘。
计算两三维矢量之间的夹角通常涉及到使用向量的点积(标量积)和模长。然而,需要注意的是,三维空间中两个非零向量的夹角是通过它们的点积和模长来定义的,而不是直接通过“向量积”来计算的,因为向量积的结果是一个向量,而不是一个标量夹角。
计算两三维矢量之间夹角的例子
例子
假设有两个三维矢量 a = ( 1 , 2 , 3 ) \mathbf{a} = (1, 2, 3) a=(1,2,3) 和 b = ( 4 , 5 , − 1 ) \mathbf{b} = (4, 5, -1) b=(4,5,−1),我们需要计算这两个矢量之间的夹角 θ \theta θ。
步骤
-
计算两个矢量的模长:
- 矢量 a \mathbf{a} a 的模长 ∣ a ∣ |\mathbf{a}| ∣a∣ 可以通过 1 2 + 2 2 + 3 2 = 1 + 4 + 9 = 14 \sqrt{1^2 + 2^2 + 3^2} = \sqrt{1 + 4 + 9} = \sqrt{14} 12+22+32=1+4+9=14 计算得到。
- 矢量 b \mathbf{b} b 的模长 ∣ b ∣ |\mathbf{b}| ∣b∣ 可以通过 4 2 + 5 2 + ( − 1 ) 2 = 16 + 25 + 1 = 42 \sqrt{4^2 + 5^2 + (-1)^2} = \sqrt{16 + 25 + 1} = \sqrt{42} 42+52+(−1)2=16+25+1=42 计算得到。
-
计算两个矢量的点积:
- 矢量 a \mathbf{a} a 和 b \mathbf{b} b 的点积 a ⋅ b \mathbf{a} \cdot \mathbf{b} a⋅b 可以通过 1 × 4 + 2 × 5 + 3 × ( − 1 ) = 4 + 10 − 3 = 11 1 \times 4 + 2 \times 5 + 3 \times (-1) = 4 + 10 - 3 = 11 1×4+2×5+3×(−1)=4+10−3=11 计算得到。
-
使用点积和模长来计算夹角:
- 根据点积的定义,我们有 a ⋅ b = ∣ a ∣ ⋅ ∣ b ∣ ⋅ cos θ \mathbf{a} \cdot \mathbf{b} = |\mathbf{a}| \cdot |\mathbf{b}| \cdot \cos \theta a⋅b=∣a∣⋅∣b∣⋅cosθ。
- 将已知的 ∣ a ∣ |\mathbf{a}| ∣a∣、 ∣ b ∣ |\mathbf{b}| ∣b∣ 和 a ⋅ b \mathbf{a} \cdot \mathbf{b} a⋅b 代入上式,得到 cos θ = a ⋅ b ∣ a ∣ ⋅ ∣ b ∣ = 11 14 ⋅ 42 \cos \theta = \frac{\mathbf{a} \cdot \mathbf{b}}{|\mathbf{a}| \cdot |\mathbf{b}|} = \frac{11}{\sqrt{14} \cdot \sqrt{42}} cosθ=∣a∣⋅∣b∣a⋅b=14⋅4211。
- 最后,使用反余弦函数 arccos \arccos arccos 来求出 θ \theta θ,即 θ = arccos ( 11 14 ⋅ 42 ) \theta = \arccos\left(\frac{11}{\sqrt{14} \cdot \sqrt{42}}\right) θ=arccos(14⋅4211)。
数值结果
由于这里涉及到无理数的运算,我们通常会使用计算器或编程软件来得到数值结果。经过计算,我们得到 θ \theta θ 的弧度值,然后可以将其转换为度。但在这里,我直接给出转换后的度数结果(注意:这个结果是近似的,因为 arccos \arccos arccos 的结果是一个无限不循环小数):
θ ≈ arccos ( 11 14 ⋅ 42 ) × 180 π ≈ 22.2 4 ∘ \theta \approx \arccos\left(\frac{11}{\sqrt{14} \cdot \sqrt{42}}\right) \times \frac{180}{\pi} \approx 22.24^\circ θ≈arccos(14⋅4211)×π180≈22.24∘
因此,矢量 a = ( 1 , 2 , 3 ) \mathbf{a} = (1, 2, 3) a=(1,2,3) 和 b = ( 4 , 5 , − 1 ) \mathbf{b} = (4, 5, -1) b=(4,5,−1) 之间的夹角约为 22.2 4 ∘ 22.24^\circ 22.24∘。
通过单位矢量计算标量积
两个三维矢量 a = ( 1 , 0 , 3 ) \mathbf{a} = (1, 0, 3) a=(1,0,3) 和 b = ( 2 , − 5 , 1 ) \mathbf{b} = (2, -5, 1) b=(2,−5,1)
- 标量积= 1 × 2 + 0 × ( − 5 ) + 3 × 1 = 5 1\times2+0\times(-5)+3\times1=5 1×2+0×(−5)+3×1=5
前面以及上述都通过分量计算 - 下面是通过单位矢量计算,还是这两个矢量的标量积。
a ⃗ = 1 i ⃗ + 3 k ⃗ , b ⃗ = 2 i ⃗ − 5 j ⃗ + 1 k ⃗ ( 1 i ⃗ + 3 k ⃗ ) ( 2 i ⃗ − 5 j ⃗ + 1 k ⃗ ) = ( 1 i ⃗ ) ( 2 i ⃗ ) + ( 1 i ⃗ ) ( − 5 j ⃗ ) + ( 1 i ⃗ ) ( 1 k ⃗ ) + ( 3 k ⃗ ) ( 2 i ⃗ ) + ( 3 k ⃗ ) ( − 5 j ⃗ ) + ( 3 k ⃗ ) ( 1 k ⃗ ) 根据前面公式 a ⃗ ⋅ b ⃗ = ∣ a ∣ ∣ b ∣ c o s α ( 1 i ⃗ ) ( 2 i ⃗ ) , ( 3 k ⃗ ) ( 1 k ⃗ ) 它们与 X 轴平行或重合, α 为 0 ∘ , c o s ( 0 ∘ ) = 1 其它全部垂直,因为分别处于不同坐标轴上, α 为 9 0 ∘ , c o s ( 9 0 ∘ ) = 0 。 ( 1 i ⃗ ) ( 2 i ⃗ ) × 1 + ( 3 k ⃗ ) ( 1 k ⃗ ) × 1 = 1 × 2 + 0 × ( − 5 ) + 3 × 1 = 5 \vec a=1\vec i+3\vec k,\vec b=2\vec i - 5\vec j+ 1\vec k \\(1\vec i+3\vec k)(2\vec i - 5\vec j+ 1\vec k) \\=(1\vec i)(2\vec i)+(1\vec i)(- 5\vec j)+(1\vec i)(1\vec k) \\+(3\vec k)(2\vec i)+(3\vec k)(- 5\vec j)+(3\vec k)(1\vec k) \\根据前面公式\vec{a} \cdot \vec{b} =|a||b|cos\alpha \\(1\vec i)(2\vec i),(3\vec k)(1\vec k)它们与X轴平行或重合,\alpha为0^\circ,cos(0^\circ)=1 \\其它全部垂直,因为分别处于不同坐标轴上,\alpha为90^\circ,cos(90^\circ)=0。 \\(1\vec i)(2\vec i)\times1+(3\vec k)(1\vec k)\times1=1\times2+0\times(-5)+3\times1=5 a=1i+3k,b=2i−5j+1k(1i+3k)(2i−5j+1k)=(1i)(2i)+(1i)(−5j)+(1i)(1k)+(3k)(2i)+(3k)(−5j)+(3k)(1k)根据前面公式a⋅b=∣a∣∣b∣cosα(1i)(2i),(3k)(1k)它们与X轴平行或重合,α为0∘,cos(0∘)=1其它全部垂直,因为分别处于不同坐标轴上,α为90∘,cos(90∘)=0。(1i)(2i)×1+(3k)(1k)×1=1×2+0×(−5)+3×1=5 - 我们要计算 cos ( 0 ∘ ) \cos(0^\circ) cos(0∘) 的值。
首先,我们需要知道在单位圆上,角度 0 ∘ 0^\circ 0∘ 对应的点是在哪里。
在单位圆上,当角度为 0 ∘ 0^\circ 0∘ 时,这个点正好位于x轴的正半轴上,并且与圆心的距离(也就是半径)为1。
根据三角函数的定义, cos \cos cos 函数表示的是单位圆上某一点到x轴的距离(也就是该点的x坐标)除以半径。
因为在这个特殊的角度 0 ∘ 0^\circ 0∘ 下,该点就在x轴上,所以它的y坐标为0,而x坐标(也就是到x轴的距离)为1,半径也为1。
所以, cos ( 0 ∘ ) = x 坐标 半径 = 1 1 = 1 \cos(0^\circ) = \frac{x坐标}{半径} = \frac{1}{1} = 1 cos(0∘)=半径x坐标=11=1。
故答案为: 1 1 1。 - 我们要计算 cos ( 9 0 ∘ ) \cos(90^\circ) cos(90∘) 的值。
首先,我们需要知道在单位圆上,角度 9 0 ∘ 90^\circ 90∘ 对应的点是在哪里。
在单位圆上,当角度为 9 0 ∘ 90^\circ 90∘ 时,这个点正好位于y轴的正半轴上。
根据三角函数的定义, cos \cos cos 函数表示的是单位圆上某一点到x轴的距离(也就是该点的x坐标)除以半径。
因为在这个特殊的角度 9 0 ∘ 90^\circ 90∘ 下,该点位于y轴上,所以它的x坐标为0。
因此, cos ( 9 0 ∘ ) = x 坐标 半径 = 0 1 = 0 \cos(90^\circ) = \frac{x坐标}{半径} = \frac{0}{1} = 0 cos(90∘)=半径x坐标=10=0。
故答案为: 0 0 0。
矢量(向量)的向量积(也称为叉积、外积或叉乘)
矢量(向量)的向量积(叉积、外积)是三维空间中两个矢量的运算,其结果是一个新的矢量,这个新矢量与原来的两个矢量都垂直。
性质
是线性代数和向量分析中的一个重要概念,它涉及到两个三维矢量的运算,并返回一个与这两个矢量都垂直的矢量。设有两个三维矢量 a \mathbf{a} a 和 b \mathbf{b} b,它们的向量积通常表示为 a × b \mathbf{a} \times \mathbf{b} a×b。以下是矢量向量积的一些主要性质:
-
垂直性:
- 向量积 a × b \mathbf{a} \times \mathbf{b} a×b 的结果是一个矢量,该矢量与 a \mathbf{a} a 和 b \mathbf{b} b 都垂直。
-
模长与夹角:
- ∣ a × b ∣ = ∣ a ∣ ⋅ ∣ b ∣ ⋅ sin θ |\mathbf{a} \times \mathbf{b}| = |\mathbf{a}| \cdot |\mathbf{b}| \cdot \sin \theta ∣a×b∣=∣a∣⋅∣b∣⋅sinθ,其中 θ \theta θ 是 a \mathbf{a} a 和 b \mathbf{b} b 之间的夹角( 0 ≤ θ ≤ π 0 \leq \theta \leq \pi 0≤θ≤π)。这个公式揭示了向量积的模长与两矢量模长及它们之间夹角的关系。
-
分配律:
- a × ( b + c ) = a × b + a × c \mathbf{a} \times (\mathbf{b} + \mathbf{c}) = \mathbf{a} \times \mathbf{b} + \mathbf{a} \times \mathbf{c} a×(b+c)=a×b+a×c(注意,这与标量积的分配律相似,但只适用于加法)。
-
反交换律:
- a × b = − b × a \mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a} a×b=−b×a(与标量积的交换律不同,向量积不满足交换律,但满足反交换律)。
-
零矢量:
- a × a = 0 \mathbf{a} \times \mathbf{a} = \mathbf{0} a×a=0(任何矢量与其自身的向量积都是零矢量)。
- 如果 a \mathbf{a} a 和 b \mathbf{b} b 平行(即 θ = 0 \theta = 0 θ=0 或 θ = π \theta = \pi θ=π),则 a × b = 0 \mathbf{a} \times \mathbf{b} = \mathbf{0} a×b=0。
-
右手定则:
- 向量积的方向可以通过右手定则来确定:将右手的四指从 a \mathbf{a} a 指向 b \mathbf{b} b,则大拇指所指的方向就是 a × b \mathbf{a} \times \mathbf{b} a×b 的方向。
-
与标量的乘法:
- ( k a ) × b = k ( a × b ) = a × ( k b ) (k\mathbf{a}) \times \mathbf{b} = k(\mathbf{a} \times \mathbf{b}) = \mathbf{a} \times (k\mathbf{b}) (ka)×b=k(a×b)=a×(kb),其中 k k k 是任意标量。即,标量可以“穿过”向量积。
-
三重积的展开:
- a ⋅ ( b × c ) \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) a⋅(b×c) 是一个标量,称为三重积或混合积,它等于以 a \mathbf{a} a、 b \mathbf{b} b、 c \mathbf{c} c 为边的平行六面体的体积。这个标量也满足某些恒等式,如 a ⋅ ( b × c ) = b ⋅ ( c × a ) = c ⋅ ( a × b ) \mathbf{a} \cdot (\mathbf{b} \times \mathbf{c}) = \mathbf{b} \cdot (\mathbf{c} \times \mathbf{a}) = \mathbf{c} \cdot (\mathbf{a} \times \mathbf{b}) a⋅(b×c)=b⋅(c×a)=c⋅(a×b)。
向量积在物理学和工程学中有着广泛的应用,例如在电磁学中计算洛伦兹力、在力学中计算力矩等。
如何计算矢量向量积
矢量(向量)的向量积(也称为叉积或外积)是三维空间中两个向量的一个重要运算,其结果是一个向量,这个向量垂直于原来两个向量所构成的平面。
假设有两个三维向量 A ⃗ = ( A x , A y , A z ) \vec{A} = (A_x, A_y, A_z) A=(Ax,Ay,Az) 和 B ⃗ = ( B x , B y , B z ) \vec{B} = (B_x, B_y, B_z) B=(Bx,By,Bz),它们的向量积 C ⃗ = A ⃗ × B ⃗ \vec{C} = \vec{A} \times \vec{B} C=A×B 可以通过以下方式计算:
C ⃗ = ( A y B z − A z B y , A z B x − A x B z , A x B y − A y B x ) \vec{C} = (A_yB_z - A_zB_y, A_zB_x - A_xB_z, A_xB_y - A_yB_x) C=(AyBz−AzBy,AzBx−AxBz,AxBy−AyBx)
这里, C ⃗ \vec{C} C 的三个分量分别是:
- C x = A y B z − A z B y C_x = A_yB_z - A_zB_y Cx=AyBz−AzBy
- C y = A z B x − A x B z C_y = A_zB_x - A_xB_z Cy=AzBx−AxBz
- C z = A x B y − A y B x C_z = A_xB_y - A_yB_x Cz=AxBy−AyBx
这个运算满足右手定则,即如果你将右手的四指从 A ⃗ \vec{A} A 旋转到 B ⃗ \vec{B} B(以小于180度的角度),那么大拇指的方向就是 A ⃗ × B ⃗ \vec{A} \times \vec{B} A×B 的方向。
示例
假设有两个向量 A ⃗ = ( 1 , 2 , 3 ) \vec{A} = (1, 2, 3) A=(1,2,3) 和 B ⃗ = ( 4 , 5 , 6 ) \vec{B} = (4, 5, 6) B=(4,5,6),计算它们的向量积:
C ⃗ = A ⃗ × B ⃗ = ( 2 × 6 − 3 × 5 , 3 × 4 − 1 × 6 , 1 × 5 − 2 × 4 ) = ( 12 − 15 , 12 − 6 , 5 − 8 ) = ( − 3 , 6 , − 3 ) \vec{C} = \vec{A} \times \vec{B} = (2 \times 6 - 3 \times 5, 3 \times 4 - 1 \times 6, 1 \times 5 - 2 \times 4) = (12 - 15, 12 - 6, 5 - 8) = (-3, 6, -3) C=A×B=(2×6−3×5,3×4−1×6,1×5−2×4)=(12−15,12−6,5−8)=(−3,6,−3)
所以, A ⃗ × B ⃗ = ( − 3 , 6 , − 3 ) \vec{A} \times \vec{B} = (-3, 6, -3) A×B=(−3,6,−3)。
例子
假设有两个三维矢量 a = ( 1 , 2 , 3 ) \mathbf{a} = (1, 2, 3) a=(1,2,3) 和 b = ( 4 , 5 , 6 ) \mathbf{b} = (4, 5, 6) b=(4,5,6),我们需要计算这两个矢量的向量积 a × b \mathbf{a} \times \mathbf{b} a×b。
步骤
-
使用行列式方法:
向量积 a × b \mathbf{a} \times \mathbf{b} a×b 可以通过一个 3x3 行列式来计算,其中 a \mathbf{a} a 和 b \mathbf{b} b 的坐标作为行列式的前两行,而第三行是单位向量 i = ( 1 , 0 , 0 ) \mathbf{i} = (1, 0, 0) i=(1,0,0), j = ( 0 , 1 , 0 ) \mathbf{j} = (0, 1, 0) j=(0,1,0), k = ( 0 , 0 , 1 ) \mathbf{k} = (0, 0, 1) k=(0,0,1) 的循环。具体地,a × b = ∣ i j k 1 2 3 4 5 6 ∣ \mathbf{a} \times \mathbf{b} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & 2 & 3 \\ 4 & 5 & 6 \end{vmatrix} a×b= i14j25k36
这个行列式按 i \mathbf{i} i, j \mathbf{j} j, k \mathbf{k} k 的顺序展开为:
a × b = ( 2 ⋅ 6 − 3 ⋅ 5 ) i − ( 1 ⋅ 6 − 3 ⋅ 4 ) j + ( 1 ⋅ 5 − 2 ⋅ 4 ) k \mathbf{a} \times \mathbf{b} = (2 \cdot 6 - 3 \cdot 5) \mathbf{i} - (1 \cdot 6 - 3 \cdot 4) \mathbf{j} + (1 \cdot 5 - 2 \cdot 4) \mathbf{k} a×b=(2⋅6−3⋅5)i−(1⋅6−3⋅4)j+(1⋅5−2⋅4)k
-
计算每个分量:
- 2 ⋅ 6 − 3 ⋅ 5 = 12 − 15 = − 3 2 \cdot 6 - 3 \cdot 5 = 12 - 15 = -3 2⋅6−3⋅5=12−15=−3( i \mathbf{i} i 分量)
- 1 ⋅ 6 − 3 ⋅ 4 = 6 − 12 = − 6 1 \cdot 6 - 3 \cdot 4 = 6 - 12 = -6 1⋅6−3⋅4=6−12=−6( j \mathbf{j} j 分量)
- 1 ⋅ 5 − 2 ⋅ 4 = 5 − 8 = − 3 1 \cdot 5 - 2 \cdot 4 = 5 - 8 = -3 1⋅5−2⋅4=5−8=−3( k \mathbf{k} k 分量)
-
组合成结果向量:
- 因此, a × b = ( − 3 , − 6 , − 3 ) \mathbf{a} \times \mathbf{b} = (-3, -6, -3) a×b=(−3,−6,−3)。
最终结果
所以,矢量 a = ( 1 , 2 , 3 ) \mathbf{a} = (1, 2, 3) a=(1,2,3) 和 b = ( 4 , 5 , 6 ) \mathbf{b} = (4, 5, 6) b=(4,5,6) 的向量积是 a × b = ( − 3 , − 6 , − 3 ) \mathbf{a} \times \mathbf{b} = (-3, -6, -3) a×b=(−3,−6,−3)。
注意
- 向量积的结果是一个矢量,其方向垂直于 a \mathbf{a} a 和 b \mathbf{b} b 所在的平面,并且遵循右手定则。
- 向量积的模长 ∣ a × b ∣ |\mathbf{a} \times \mathbf{b}| ∣a×b∣ 等于 ∣ a ∣ ⋅ ∣ b ∣ ⋅ sin θ |\mathbf{a}| \cdot |\mathbf{b}| \cdot \sin \theta ∣a∣⋅∣b∣⋅sinθ,其中 θ \theta θ 是 a \mathbf{a} a 和 b \mathbf{b} b 之间的夹角。但在这个例子中,我们直接计算了向量积的每个分量,而没有使用模长和夹角。
- 向量积不满足交换律,即 a × b = − b × a \mathbf{a} \times \mathbf{b} = -\mathbf{b} \times \mathbf{a} a×b=−b×a。
单位矢量
性质
- 模长为1:单位矢量的模长总是等于1。
- 方向性:单位矢量仅表示方向,不表示大小。
- 无量纲:由于模长为1,单位矢量在数值上通常是无量纲的,尽管它们可能用于表示具有特定物理量纲的矢量的方向。
示例
假设在二维空间中有一个矢量 A ⃗ = 3 i ^ + 4 j ^ \vec{A} = 3\hat{i} + 4\hat{j} A=3i^+4j^,其中 i ^ \hat{i} i^和 j ^ \hat{j} j^分别是沿x轴和y轴的单位矢量。
- 矢量 A ⃗ \vec{A} A的模长为:
∣ A ⃗ ∣ = 3 2 + 4 2 = 5 |\vec{A}| = \sqrt{3^2 + 4^2} = 5 ∣A∣=32+42=5
- 因此,矢量 A ⃗ \vec{A} A的单位矢量为:
A ^ = A ⃗ ∣ A ⃗ ∣ = 3 i ^ + 4 j ^ 5 = 3 5 i ^ + 4 5 j ^ \hat{A} = \frac{\vec{A}}{|\vec{A}|} = \frac{3\hat{i} + 4\hat{j}}{5} = \frac{3}{5}\hat{i} + \frac{4}{5}\hat{j} A^=∣A∣A=53i^+4j^=53i^+54j^
这个单位矢量 A ^ \hat{A} A^表示了与 A ⃗ \vec{A} A相同的方向,但大小(或模长)为1。
应用
单位矢量在多个领域中有广泛应用,包括:
- 物理学:用于表示力、速度、加速度等的方向。
- 数学:在向量分析、线性代数和微分几何中,单位矢量用于定义方向导数、切向量等。
- 工程学:在机械、电气和航空航天工程中,单位矢量用于描述物体的运动方向和力的方向。
总之,单位矢量是理解和描述矢量方向的重要工具。
矢量的位移
是描述物体位置变化的一个物理量,它既有大小又有方向,因此是一个矢量。在物理学中,位移通常用大写字母 s ⃗ \vec{s} s 或 Δ r ⃗ \Delta \vec{r} Δr 来表示,其中 s ⃗ \vec{s} s 表示位移矢量, Δ r ⃗ \Delta \vec{r} Δr 表示位置矢量的变化量。
定义
位移是物体从初位置指向末位置的有向线段。这个有向线段的长度表示位移的大小,而有向线段的方向则表示位移的方向。
计算公式
在直角坐标系中,如果物体的初位置坐标为 ( x 1 , y 1 , z 1 ) (x_1, y_1, z_1) (x1,y1,z1),末位置坐标为 ( x 2 , y 2 , z 2 ) (x_2, y_2, z_2) (x2,y2,z2),则位移矢量 s ⃗ \vec{s} s 可以用以下公式表示:
s ⃗ = Δ r ⃗ = ( x 2 − x 1 ) i ^ + ( y 2 − y 1 ) j ^ + ( z 2 − z 1 ) k ^ \vec{s} = \Delta \vec{r} = (x_2 - x_1) \hat{i} + (y_2 - y_1) \hat{j} + (z_2 - z_1) \hat{k} s=Δr=(x2−x1)i^+(y2−y1)j^+(z2−z1)k^
其中, i ^ \hat{i} i^、 j ^ \hat{j} j^、 k ^ \hat{k} k^ 分别是沿 x x x、 y y y、 z z z 轴方向的单位矢量。
性质
- 矢量性:位移是矢量,具有大小和方向。
- 相对性:位移是相对的,它依赖于所选择的参考系。
- 路径无关性:位移只与物体的初末位置有关,与物体经过的路径无关。
- 可加性:如果物体连续进行两段位移,则总位移等于这两段位移的矢量和。
应用
位移在物理学中有着广泛的应用,如描述物体的运动状态、计算物体的平均速度等。在解决具体问题时,我们通常需要先确定物体的初末位置,然后计算位移矢量。
示例
假设一个物体在二维平面上从点 A ( 1 , 2 ) A(1, 2) A(1,2) 移动到点 B ( 4 , 6 ) B(4, 6) B(4,6),求物体的位移矢量。
解:根据位移的计算公式,我们有
s ⃗ = ( 4 − 1 ) i ^ + ( 6 − 2 ) j ^ = 3 i ^ + 4 j ^ \vec{s} = (4 - 1) \hat{i} + (6 - 2) \hat{j} = 3 \hat{i} + 4 \hat{j} s=(4−1)i^+(6−2)j^=3i^+4j^
因此,物体的位移矢量是 3 i ^ + 4 j ^ 3 \hat{i} + 4 \hat{j} 3i^+4j^,表示物体沿 x x x 轴方向移动了 3 个单位,沿 y y y 轴方向移动了 4 个单位。
参考文献
1.《物理学基础》
2. 文心一言
3. chatgpt