C生万物 函数的讲解与剖析【内附众多案例详解】
printf("交换前:a = %d, b = %d\n",a, b);
swap(a, b);
printf("交换后:a = %d, b = %d\n", a, b);
return 0;
}
* 来看一下运行结果。可以看到两个数并没有发生交换
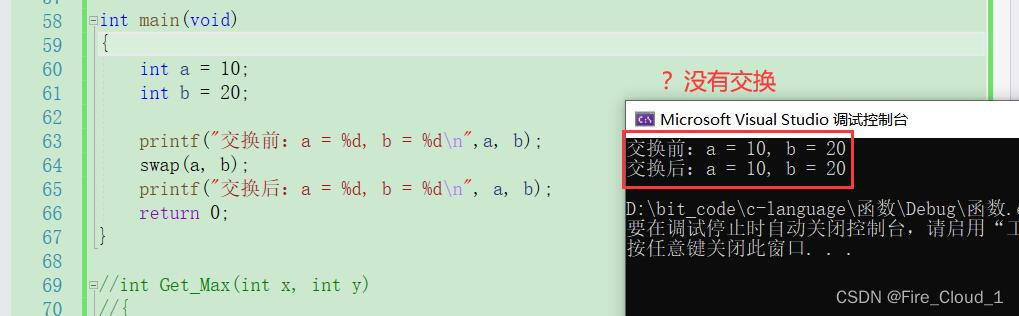
* 那有小伙伴就很诧异,这是为什么呢?我们一起来调试分析一下



* 上面是笼统地看,我们通过地址再来看看

**你可以这么认为:形参实例化之后其实相当于实参的一份临时拷贝**
* 上面这一个,叫做【传值调用】,函数内部形参的修改是不会影响实参的,接下来我们来讲讲【传址调用】
* 虽然指针这一块我还没有讲到,但是我在[初始C语言]( )那块儿已经有讲到指针这个内容了,如果不了解的可以先去看看一下。因为真正地修改一个函数外部的实参值,我们只能使用对指针进行解引用来进行修改,然后如果你继续学下去的话还可以使用【二级指针】【C++引用】的方式,也是可以做到的,这里我就讲一级指针接收地址这一块
void swap(int* px, int* py)
{
int t = *px;
*px = *py;
*py = t;
}
* 先看一下代码,然后我们再通过DeBug来展开分析一下



* 最后来看一下运行结果

讲到这里,相信你对这个案例应该有了一个深刻的理解了
## 三、函数的参数
### 1、实际参数(实参)
>
> 真实传给函数的参数,叫**实参**
>
>
>
* 对于实参而言,它可以是【常量】、【变量】、【表达式】、【函数】等。我们到VS里来测试一下

* 无论实参是何种类型的量,在进行函数调用时,它们都必须有**确定的值**,以便把这些值传送给形参
### 2、形式参数(形参)
* 形式参数是指函数名后括号中的变量,因为形式参数只有在函数**被调用的过程中才实例化**(分配内存单元),所以叫形式参数。形式参数当函数调用完成之后就**自动销毁**了。因此形式参数只在函数中有效。
所以我们可以总结出来一句话:
**【函数调用时,实参传递给形参,形参是实参的一份临时拷贝,形参的改变不影响实参】**
## 四、函数的调用
这里我们再来说一下函数的【传值调用】和【传址调用】,这一块在上面的案例中也涉及到了
### 1、传值调用
>
> 函数的形参和实参分别占有不同内存块,对形参的修改不会影响实参
>
>
>

### 2、传址调用
>
> 传址调用是把函数外部创建变量的**内存地址**传递给函数参数的一种调用函数的方式。
> 这种传参方式可以让函数和函数外边的变量**建立起真正的联系**,也就是函数内部可以**直接操**作函数外部的变量。
>
>
>

### 3、专项练习
>
> 看了这么多,接下来就要来实践一下了,我们通过四道练习题来进行训练
>
>
>
#### 3.1 素数判断
* 首先是对于素数的一个判断。【素数】又叫质数。素数,指的是“大于1的整数中,只能被1和这个数本身整除的数”
* 知道了规则,那代码就好写了。我们来输出一下1~100的所有素数。在外部写一个循环,就可以获取1 - 100之间的数字了,然后对于素数的求解,**可以单独封装为一个函数**
---
* 首先来思考需要传入哪些参数,很明显:只需要传入被判断的数字即可,然后就要去思考这个函数的返回值,可以这样设定:在函数内部若是判断出其为素数,那么就返回1,否则就返回0,然后在主函数外部进行一个判断即可
for (int i = 1; i <= 100; ++i)
{
if (IsPrime(i) == 1)
{
printf(“%d是素数\n”,i);
}
}
* 接下去我们来看看函数的部分
/*素数判断*/
int IsPrime(int n)
{
if (n <= 1)
return 0;
else if (n == 2)
return 1;
else
{
for (int i = 2; i < sqrt(n) + 1; ++i)
{
if (n % i == 0)
{
return 0;
}
}
}
return 1;
}
* 抛开其他部分,我们先来看主体,思考一下为什么这个循环的结束条件我要写成`sqrt(n) + 1`,当然这里是开区间,你也可以写成闭区间的形式`<= sqrt(n)` ,设想一下一个数`16 = 2 * 8`,16还可以表示成`16 = 4 * 4`,那我们就可以发现,若是找到一个16的公因子【2】,其实就可以不做判断了,直接return 0即可,`sqrt(n)` 其实就相当于这个【4】,前面的2已经到了,我们就可以这个算数平方根作为分解点,不需要再往下找了
* 再举一个例子`9 = 3 * 3`,`sqrt(9) = 3`,我们在进行判断的时候,i为3时其实就不需要在向下判断了,因为9对3取余为0,因此【9】就不是一个素数了,这么说你应该可能明白了,素数判断的方法有很多种,大家主要先记住这一种即可
for (int i = 2; i < sqrt(n) + 1; ++i)
{
if (n % i == 0)
{
return 0;
}
}
* 然后其他的部分就是对于特殊情况的判断,也就是【1】和【2】这两个数进行一个单独的判断
if (n <= 1)
return 0;
else if (n == 2)
return 1;
* 然后我们来看一下运行结果

#### 3.2 闰年判断
* 接下去再进行一个闰年判断的练习
* 【闰年】公历年份是4的倍数,且不是100的倍数,为普通闰年。公历年份是整百数,且必须是400的倍数才是世纪闰年
* 一样,我们先将主函数写好。需求是输出一下1000~2000之间的所有闰年
for (int i = 1000; i <= 2000; ++i)
{
if (Isleap(i) == 1)
{
printf("%d ", i);
}
}
* 然后的各方面条件和上面是一样的,便不做详解,我们来看看函数体
* 这一块我给出两种方法,第一种就是直接了当一些,若是能被4整数但是不能被100整数,或者可以被400整数的数,那就是一个闰年,此时返回1即可,反之返回0,利用到了【**逻辑操作符**】
* 第二种方法就是一个if的嵌套判断,这里要注意的一点是对400取余的条件外面要写成【if】,不要写成【else if】,否则两个判断条件就只会进去一个了,那就回漏掉几个年份
/*闰年判断*/
int Isleap(int year)
{
//Way1
//if ((year % 4 == 0 && year % 100 != 0) || (year % 400 == 0))
//{
// return 1;
//}
//return 0;
//Way2
if (year % 4 == 0)
{
if (year % 100 != 0)
{
return 1;
}
}
if (year % 400 == 0)
return 1;
}
* 来看一下运行结果

#### 3.3 二分查找
* 接下去来做一道很经典的题目 ——>【二分查找】
* 首先我们需要设定一个有序数组,因为二分查找只能在序列有序的情况下才可以进行
int arr[] = { 1,2,3,4,5,6,7,8,9 };
int sz = sizeof(arr) / sizeof(arr[0]);
int k = 7;
* 可以看到,上面除了设定数组以外,我还求出这个数组的元素个数,因为在进行函数传参的时候需要使用到
int pos = BinarySearch(arr, sz, k);
* 来看如何传值以及接收返回值,首先我们需要将这个数组的【首元素地址】传入,因为对于一个数组而言,你无法将整个数组都传入函数体中,只能传入这个函数的首元素的地址,那既然是地址,就可以使用**指针**来进行接收,当然最具有可读性的还是数组接收数组,若是你不知道传入的这个是数组的首元素地址,那可能用指针来接受就有点晦涩难懂了
* 除了要传入数组的首元素地址之外,还需要传入我在上面求出来的【sz】,也就是数组的个数,这一点的话很重要,对于数组的大小一定要在外面求解完再传进去,若是你在函数内部求解数组的大小时,因为传入的是数组的首元素地址,因此`sizeof(arr)`和`sizeof(arr[0])` 就都是一样的4个字节,因为整型元素都是4个字节的大小,所以求出的sz就为【1】了,此时就会发生问题。最后的话需要查找的值肯定也需要进行一个传入
//int BinarySearch(int* a, int n, int k) //指针接收地址
int BinarySearch(int a[], int n, int k) //数组接收数组
{
int left = 0;
int right = n - 1;
while (left <= right)
{
int mid = left + (right - left) / 2;
if (k > a[mid])
left = mid + 1;
else if (k < a[mid])
right = mid - 1;
else
return mid;
}
return -1;
}
* 对于二分查找这一块可以看看我的另一篇文章 ——> [二分法与折半插入排序]( )
#### 3.4 修改数值
* 接下去一个练习就是通过函数内部的修改带动函数外部数组的修改,这里就要使用到我们上面所说的【传址调用】。先来看看代码
void change(int* px)
{
(*px)++;
}
int num = 0;
change(&num);
printf(“num = %d\n”, num);
* 在函数外部,我传入了num值的地址,然后在函数体的形参中使用指针来进行接收,此时对这个指针进行解引用就可以获取到外部的实参,就可以直接对其进行修改了,这里主要写成`(*px)++`,不能写成`*px++`,因为【++】的优先级比【\*】来得高,所以会先对这个指针变量进行一个++,然后再对其进行一个解引用的操作,但是当这个指针后移的时候,就已经变成了野指针,此时再去访问这个野指针就会出现问题,后面给出运行结果
* 可以其进行一次的修改,那一定也可以进行多次的修改,我们通过运行结果来看看

* 但是我们上`*px`外的括号去掉再看看

## 五、函数的嵌套调用和链式访问
### 1、嵌套调用
>
> 函数和函数之间可以根据实际的需求进行组合的,也就是互相调用的
>
>
>
* 首先来看第一个例子。非常好理解,可以自己看看
void print()
{
printf(“haha\n”);
}
void three()
{
for (int i = 0; i < 3; ++i)
{
print();
}
}
int main(void)
{
three();
return 0;
}

函数可以嵌套调用,但是不能嵌套定义
### 2、链式访问
>
> 把一个函数的返回值作为另外一个函数的参数
>
>
>
* 这里我先介绍一下【[strlen]( )】这个函数

* 对于`strlen()`和`sizeof()`我会在后面的【面试题】专栏中进行细致讲解
* 然后我们到代码里面来用一下
char a[] = “hello world”;
int len = strlen(a);
printf(“len = %d\n”, len);

这里要注意一点的是strlen()去求字符串长度的时候是不算’\0’的
* 接着再来介绍一个函数【[strcat]( )】

* 好,接下去我们来看看如何做到链式访问
char a[10] = “hello”;
int len = strlen(strcat(a, “bit”));
printf(“len = %d\n”, len);

* 接下去再来看一下链式访问的例子。你知道这句代码输出的结果是多少吗
printf(“%d”, printf(“%d”, printf(“43”)));
* 来揭晓一下结果吧

* 那有同学就很诧异,为什么这句代码的输出是【4321】呢,我们来看一下【[printf]( )】这个函数

* 可以看到对于printf的返回值是输出字符的个数,那这就可以解释通了:对于内层的 `printf("43")`输出的字符个数有2个,然后再看外层的`printf("%d", printf("43"))`便会在输出一个2,它的返回值就是输出了一个字符,那么整体的这个`printf("%d", printf("%d", printf("43")))`就会在输出一个1,作为返回值

## 六、函数的声明和定义
### 1、函数声明
>
> 1. 告诉编译器有一个函数叫什么,参数是什么,返回类型是什么。但是具体是不是存在,函数
> 声明决定不了。
> 2. 函数的声明一般出现在**函数的使用之前**。要满足先声明后使用。
> 3. 函数的声明一般要放在**头文件**中的
>
>
>
* 来看一下代码
int Add(int x, int y);
int main(void)
{
int a = 0;
int b = 0;
scanf(“%d %d”, &a, &b);
int sum = Add(a, b);
printf("sum = %d\n", sum);
return 0;
}
int Add(int x, int y)
{
return x + y;
}

### 2、函数定义
>
> 函数的定义是指函数的具体实现,交待函数的功能实现
>
>
>
* 对于上面的代码,我们可以对其做一个分解,将【add】这个功能单独放到一个.c的文件中,然后再写一个.h的文件去声明一下这个函数。因为在日常的项目工程中,是有很多程序员一起写代码的,但是他们不可能在一个.c文件中一起书写,也不能等一个人写好之后另一个人再接着写,这样就会降低开发效率
* 所以我们就有一个分模块编写的说法,也就是在一个头文件中先写好函数的声明和各种库函数的引用和定义,然后每个程序员都可以创立自己的.c文件,然后去书写自己的那段逻辑,最后将大家的代码进行一个整合,就完成了整个项目

* 上面就是对【add】整个功能做了一个分模块的编写。在后面学到三子棋和扫雷的时候还会教大家用这种分模块编写
## 七、函数递归
接下去我们来说说函数递归,这也是函数这一块最难理解的内容
### 1、什么是函数递归?
>
> 程序调用自身的编程技巧称为递归( recursion)
> 只需少量的程序就可描述出解题过程所需要的多次重复计算,**大大地减少了程序的代码量**
> **递归的主要思考方式在于:把大事化小**
>
>
>
### 2、函数递归的两个必要条件
* 存在**限制条件**,当满足这个限制条件的时候,递归便不再继续。
* 每次递归调用之后越**来越接近**这个限制条件
### 3、题目的展开与剖析
#### 3.1 例题1:打印数字
【需求】:输入1234,打印1 2 3 4
* 在之前我们学习分支和循环的时候有做过类似的题目,那个时候我们是利用取余【%】和整除【/】倒着打印一个数字的每个数位,也就是下面这段代码
void print1(int num)
{
while (num > 0)
{
printf("%d ", num % 10);
num /= 10;
}
}
**运行结果如下**

* 但是呢,现在我们要顺着将这个数的每一个数位进行一个打印,这该怎么去做呢?我们来分析一下
* 我们在屏幕上通过scanf输入一个数,然后通过封装好的一个函数传入`print(num)`,即`print(1234)`,那既然上面讲到了这个分割数字的思路,这里我们也可以使用这个思路来完成,
* 对于`print(1234)`我们可以拆成`print(123) 4`
* 对于`print(123)`又可以拆成`print(12) 3`
* 对于`print(12)`又可以拆成`print(1) 2`
* 那`print(1234)`就被拆成了`print(1) 2 3 4`,也就是当这个num < 10为一个个位数时,就做一个打印,否则的话就不断将其以十分之一倍得进行缩小。我们将其转化为代码的形式就【一目了然】了
* 可以看到,这里是使用到了一个递归的逻辑,上面说到递归都是具有结束条件的,若是不符合的话就层层递归下去,知道当前传入的num值为个位数为止才进行一个回调
void print2(int num)
{
if (num > 9)
{
print2(num / 10);
}
printf("%d ", num % 10);
}
**运行结果如下**

* 可能还是有同学对于递归有点难理解,没关系,我们通过递归展开图再来看看

* 通过这么一幅递归展开图的剖析,相信你对函数递归的整体流程应该有了一个了解。但是还是觉得难以有这个思维,没事我们再来看一道例题
#### 3.2 例题2:求字符串长度
【需求】:输入abc,输出其长度为3
* 上面有讲到过strlen()这个函数,其可以求出一个字符串的长度,我们首先通过这个函数来试试。运行结果后面再给出
int main(void)
{
char str[] = “abc”;
int len = strlen(str); //利用库函数进行求解
printf("len = %d\n", len);
return 0;
}
* 可以看到,这个很简单,但是不要忘了包含头文件【string.h】
* 接下去的话我们将这个**strlen**()函数改成**my\_strlen()**,我们自己来实现一下这个底层的逻辑。对于`int len = my_strlen(str);`,我们传入了字符数组str的首元素地址,那上面有讲到过对于地址要使用指针来进行接收,最后还要返回求出的长度,所以对于函数我们可以定义成这样
int my_strlen(char* str)
* 接下去考虑该如何去实现和这个函数。对于str这个字符指针现在是指向传入字符数组的首元素地址,也就是【a】,那你就要搞懂对于一个字符串来说以什么作为结束标志,没错,就是【\0】,因此可以让这个字符指针不断后移,每一次对其进行解引用看看是否为【\0】即可,有了思路我们就可以写出代码了
* 在这里的话还需要设置计数器,我们我们要去求解这个字符串的长度,因此判断到它不为【\0】的时候就count++,然后让这个字符指针进行后移即可。
int my_strlen(char* str)
{
int count = 0;
while ((*str) != ‘\0’)
{
count++; //计数器累加
str++; //字符指针后移
}
return count;
}
* 可是呢现在我要改变一下题目的要求,不可以使用计数器进行求解字符串的长度,那有小伙伴就很诧异了,你让我去求长度,但是连计数器都不让用,这怎么求呢,别急,我们用递归来试试
* 一样,我们可以使用到上面的分割思想
* 对于`my_strlen(abc)`我们可以拆成`1 + my_strlen(bc)`
* 对于`my_strlen(bc)`我们可以拆成`1 + my_strlen(c)`
* 对于`my_strlen(c)`我们可以拆成`1 + my_strlen('\0')`
* 那`my_strlen(abc)`就相当于是`1 + 1 + 1 + 0`。也是使用字符指针去进行一个后移,若其不为【\0】时,就不断对这个字符串进行拆分,然后直到遇到【\0】时便`return 0`。接下去就可以写出代码了
int my_strlen(char* str)
{
if (*str != ‘\0’)
{
return 1 + my_strlen(str + 1);
}
return 0;
}
* 然后来看一下结果吧,上面三段代码的结果都是一样的,所以一起展示了

* 一样,我们来画一下递归展开图

* 看了这个相信你对递归的概念又进一步有了了解。但还是感觉有所欠缺,我们再来看一道对于递归来说很经典的题目——阶乘求解
#### 3.3 例题3:阶乘求解
【需求】:输入一个数,输出其求阶乘后的结果
* 对于阶乘来说可能有小伙伴没听过的,我稍作分析然后先列出一个公式。
* 阶乘就是从从一个数开始乘,慢慢减少,一直乘到1为止,举个例子3! = 3 \* (3 - 1) \* (3 - 2) = 3 \* 2 \* 1 = 6。再举两个特殊一点的 0! = 1,1!=1 ,知道了这些,我来列出一个公式你看看

* 也就是当【n <= 1】时,即0的阶乘和1的阶乘最后都是1,当【n >= 2】时,最后的结果就是n去乘以它减1的阶乘,于是我们就可以得出递归的代码
/*阶乘——递归*/
int Func1(int n)
{
if (n <= 1)
return 1;
else
return n * Func1(n - 1);
}
* 对于阶乘来说,不仅可以使用递归实现,还可以使用循环的方式来是实现,这个我们在前面学习分支和循环语句的时候就有讲到过,这里就不作详解了
/*阶乘——循环*/
int Func2(int n)
{
int ret = 1;
for (int i = 1; i <= n; ++i)
{
ret *= i;
}
return ret;
}
这里再对上面的递归实现做一个递归展开图的分析

* 看完这三道例题,相信你对递归的代码写法有了一个初步的认识。接下去我们再通过三道练习题来巩固一下
#### 3.4 练习1:斐波那契数列
【需求】:输入一个数,输出从1到这个数的斐波那契数
* 如果有同学对斐波那契数列不太了解的,可以先去看看——> [斐波那契数列]( )。这里给出从1~10的斐波那契数列 **【1 1 2 3 5 8 13 21 34 55】**,可以看出对于1,2两个数来说都是①,后面就是数就是前两个数之和,因此我们可以列出下面的公式

* 然后根据这个公式写出代码
/*斐波那契数列——递归*/
int Fib1(int n)
{
if (n <= 2)
return 1;
else
return Fib1(n - 2) + Fib1(n - 1);
}
* 然后一样通过递归展开图来分析一下,不过对于斐波那契数列的递归展开图可能有些复杂,因为每次递归存在两个分支,这个结构如果学过数据结构的同学应该清楚是[二叉树]( ),没学过也没有关系,因为这是C语言的文章。下面是我的讲解,希望你可以看得懂

* 仔细观察其实可以发现,光是求5!这么小的数字,就有一些重复计算,也就是【1】和【2】这两个数字。包括【3】也计算了两次,那在这里其实我们可以去打印一下,若是求50的阶乘话【3】会计算几次呢
#### 3.5 练习2:青蛙跳台阶
>
> 接下去我们再来做一个很有意思的小练习,这个和斐波那契数列很像
>
>
>
① 首先来快速了解一下青蛙的跳法
**青蛙每次可以跳一个台阶或者两个跳台阶**

* 需求是算出当青蛙跳到第n个台阶的时候,有几种跳法
③ 通过画算法图来分析一下

* 可以看出,对于第n个台阶,青蛙的跳法变化规律为:**1——>2——>3——>5——>8**,很明显,呈现的就是我们上面所讲到过的【斐波那契数列】,那这就好办了
④ 来看看代码如何书写
* 首先来看看递归版的写法
//递归
int Jump(int n)
{
if (n <= 2)
return n;
else
return Jump(n - 1) + Jump(n - 2);
}
int main(void)
{
int n = 0;
printf(“请输入台阶的数量:”);
scanf(“%d”, &n);
for (int i = 0; i < n; ++i)
{
printf("跳到第%d个台阶时有%d种跳法\n", i + 1, Jump(i + 1));
}
return 0;
}
**运行结果**

* 接下去再来看看迭代版的写法
//迭代
int Jump2(int n)
{
int a = 1;
int b = 2;
int c = 1;
int t = n;
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
if (t <= 2)
return n;
else
return c;
}
**运行结果**

* 对于青蛙跳台阶和斐波那契数列很是类似,因此不做过多分析,可以自己去谢谢代码画图感受一下
#### 3.6 练习3:汉诺塔问题
>
> 汉诺塔是很经典的递归问题,我们一起来看一下
>
>
>
① 首先来了解一下【汉诺塔】是什么东西
* 汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘
② 接下去快速了解一下它的规则
**规则一:每次只能移动一片盘片**
**规则二:每次移动完后要保证小盘片在大盘片的上面**
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**
e8fb394d40bef95bddb00c7efe.jpeg#pic_center)
* 接下去再来看看迭代版的写法
//迭代
int Jump2(int n)
{
int a = 1;
int b = 2;
int c = 1;
int t = n;
while (n > 2)
{
c = a + b;
a = b;
b = c;
n--;
}
if (t <= 2)
return n;
else
return c;
}
**运行结果**

* 对于青蛙跳台阶和斐波那契数列很是类似,因此不做过多分析,可以自己去谢谢代码画图感受一下
#### 3.6 练习3:汉诺塔问题
>
> 汉诺塔是很经典的递归问题,我们一起来看一下
>
>
>
① 首先来了解一下【汉诺塔】是什么东西
* 汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘
② 接下去快速了解一下它的规则
**规则一:每次只能移动一片盘片**
**规则二:每次移动完后要保证小盘片在大盘片的上面**
[外链图片转存中...(img-gDcrzh3s-4702027633794)]
[外链图片转存中...(img-gF2RhiYK-4702027633795)]
**一个人可以走的很快,但一群人才能走的更远!不论你是正从事IT行业的老鸟或是对IT行业感兴趣的新人,都欢迎加入我们的的圈子(技术交流、学习资源、职场吐槽、大厂内推、面试辅导),让我们一起学习成长!**