【总结】字符串匹配: KMP 和 拓展KMP

 

　比起ac自动机,kmp就一个next数组,理解了如何初始化next后就可以搞一些模板题了,下面是还不错的学习资料,清晰易懂,自己用的模板也来自它:

　http://chaoswork.com/blog/2011/06/14/kmp%E7%AE%97%E6%B3%95%E5%B0%8F%E7%BB%93/

kmp模板

next[0]=-1;j=-1;
for(i=0;i<m;)
{
    while(j>=0 && p[i]!=p[j])j=next[j];
    i++;
    j++;
    next[i]=j;
}

for(i=0,flag=0,j=0;i<n;)
{
    while(j>=0 && p[j]!=t[i])j=next[j];
    i++;
    j++;//已经匹配了模式串的多少个
    if(j==m)//匹配成功
}

接下来需要更加深入地了解next数组,许多题目需要用到它的定义来预处理字符串:

 xdu 1154

显然,用2次kmp处理处前缀和后缀在各点的匹配情况,用dp记录符合要求的子串,有几个要注意的地方:(调了2个小时T_T)

1.前缀的其实位置不但要在后缀的前面,终止位置不能超过后缀的终止位置,也就是说前缀不能包含后缀.

2.　

View Code

for(i=0,flag=0,j=0;i<n;)
{
    while(j>=0 && p[j]!=t[i])j=next[j];
    i++;j++;

　　if(j==m)//若在此处记录则会出现bug,因为此时匹配完成点是i-1
}

CF也有一道与上面类似的题,需要用kmp预处理最左端前缀和最右端后缀

http://codeforces.com/contest/149/problem/E

循环节问题

它还能用来求周期字符串的循环节HDU1358:

性质:

当且仅当len%(len-next[len])==0时,str[next[len]~len-1]为最小循环节

要证明它需要说明3点:

1.一个字符串str是周期串,假设s1为它的循环节,则str=s1 s1...s1(n个) 

推导出=>len%(len-next[len])==0成立.

2.next[len]~len-1为s1 ,len%(len-next[len])==0时 

推导出=>str为周期串,s1为最小循环节

3.如何保证是最小的.

证明:

1.由next的性质知道,s[1~next[len]-1]与s[1~len-1]有最长的相等的前缀和后缀s,很显然s就是n-1个s1了.

2.设s1的长度为L,由于len%L==0 , str可以分解成若干个长度为L的小串,设它们从左到右依次为

a₁ , a₂ ... a_n

根据匹配关系得

a₁=a₂;

a₂=a₃;

..

a_n-1=a_n;

因此a₁=a₂=a₃...=a_n;

用s1表示相同的前缀和后缀,则字符串可以表示为 s1 , t , s1;

　其中t是未知的一个串,它有几种可能：

　(1) t是一个负串,即 前缀和后缀是相互渗透的.(如串 ababab 的 s1为abab)

　　　进行如下推理：这段证明有问题,因为两头阴影部分可能不相同

　　　此时s1,t,s1退化成(s1,s2)和(s2,s1)

　　　于是我们知道s1的前缀是s2,后缀也是s2,s1-s2的前缀是s2,后缀也是s2......

　　　最后利用命题2的条件len[s1]%len[s2]==0,知道s1能被分解成s2,即

　　　s1=s2 s2...s2 于是s2是s1的最小循环节(第3步来证明它是最小的)

　(2)t是一个空串,则s1, t ,s1退化成了s1,s1;于是很显然了......

　(3)t是一个有长度的串.

　那么len-next[len]=strlen(t+s1), 不能满足整除的条件.

3.next[len]保证了前缀与后缀最大化,如果循环节s1存在而s1内还有循环节s1',则next[len]可以向后移动,与定义矛盾.

 

相等的循环同构问题

hdu3374 string problem

分析:

　　最大和最小的循环同构字符串可以分开处理,求位置可以利用最小最大表示法(03wc论文 周源)

　　求出现的次数可以用kmp扫一遍,但利用 循环节 可以更快地得到答案.

性质:

　　字符串str由k个最小循环节s1组成,则它的相等循环同构数为k.

证明:

　　设相等循环同构数为p,我们可以利用循环节s1构造出k个相等的循环同构,于是p>=k;

　　下面证明p<=k:

　　　　如果p>k

　　　　假设在移动完s1到尾部前,出现了相同的循环同构串,不妨设此时移动的串为s2,

　　　　则利用 循环节性质2第1种情况的推理方法 可以知道s2为字符串的一个循环节

　　　　且s2的长度<s1,与s1为最小循环节的条件矛盾,因此p<=k.

　　于是p只能等于k.

 

拓展KMP

　　有很长一段时间单纯地以为拓展kmp只是kmp倒过来跑,后来发现很多问题其实无法转换成kmp解决,于是怒学了一下拓展kmp.

　　首先比较一下kmp和拓展kmp解决的问题:

　　kmp解决了求所有主串的前缀pre[i] (0<=i<n)的后缀与模式串前缀的最大匹配长度问题;

　　拓展kmp解决了所有主串的后缀suf[i]的前缀,与模式串前缀的最大匹配长度问题.

　　

 1 void getNext() {
 2     int l = 1, r = -1, i, j;
 3 
 4     for (next[0] = 0, i = 1; p[i]; ++i) {
 5         if (i + next[i - l] - 1 < r) next[i] = next[i - l];
 6         else {
 7             for (j = max(r - i + 1, 0); p[i + j] && p[i + j] == p[j]; ++j);
 8             next[i] = j; l = i; r = i + j - 1;
 9         }
10     }
11     next[0] = i;
12 }

 

　　设模式串为str;

　　定义next[i]为 str 与 它的后缀suf[i]的最大公共前缀长度.

　　r是当前已经确定匹配区间的最右端点,l是对应的左端点,即 r=l+next[l]-1;

　　当要求next[i]时

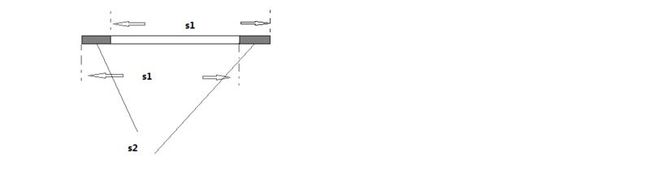
　　根据 next定义 str[ l , l+next[l]-1 ] == str[ 0 , next[l]-1 ];

　　得到 str[ i , l+next[l]-1 ] == str[ i-l , next[l]-1 ];

　　设s1=str[ i , l+next[l]-1 ]; 

　　讨论以下情况：

　　1. 若  i在 [l,r] 区间内  

　　　next[i-l]的值我们已经知道,这时候需要讨论:

　　　　如果  next[i-l] 小于 s1 的长度,那么可以知道在下标为 next[i-l] 的位置必定会失配,于是next[i]=next[i-l];

　　　　如果  next[i-l] 大于或等于 s1 的长度,那么直到r位置,我们都可以确定已经匹配上了,接下来需要确定r后面

　　　　位置的匹配情况,而此时i已经匹配了r-i+1的长度,next[i]从这个值开始计数就可以了,计数完成后i+next[i]-1

　　　　已经大于r,因此要更新   r=i+next[i]-1 , l=i ;

　　2.若 i不在[l,r]的区间内,即 i > r, 前面得到的信息无法用到,于是我们需要从头将str[i]与str[0]进行匹配,当然也要记得更新l,r.

 　  复杂度：

　　　　2个循环变量i,j都是单调增的,而他们最多增加n次,因此 复杂度是线性的.

　　拓展kmp求循环节的方法参考kmp求循环节部分.

　　知道这些后可以来解决这个问题.

　　

Revolving Digits

#include<stdio.h>
#include<string.h>
#define max(a,b) (a)>(b)?(a):(b)
#define maxn 100010
char str[maxn<<1];
int next[maxn<<1];
int len,ans[3];
void getNext()
{
    int i,j,l,r;
    l=1,r=-1;
    next[0]=0;
    for(i=1;i<2*len;i++){
        if(next[i-l]<r-i+1)next[i]=next[i-l];
        else{
                j=max(r-i+1,0);
                while(i+j<2*len && str[i+j] == str[j])
                    j++;
                l=i;r=i+j-1;next[i]=j;
            }
    }
    next[0]=i;
//    for(i=0;i<2*len;i++)printf(" %d",next[i]);
}
void statis()
{
    int i;
    memset(ans,0,sizeof(ans));
    for(i=1;i<len*2;i++){
        if(next[i]>=len)ans[1]++;
        else if(str[i+next[i]] > str[next[i]])ans[2]++;
        else if(str[i+next[i]] < str[next[i]])ans[0]++;
        if(len*2%i==0 && i+next[i]==len*2)break;
    }
    printf("%d %d %d\n",ans[0],ans[1],ans[2]);
}
int main()
{
    int cas,t;
    scanf("%d",&cas);
    for(t=1;t<=cas;t++){
        printf("Case %d: ",t);
        scanf("%s",str);
        len=strlen(str);
        memcpy(str+len,str,len);
        getNext();
        statis();
    }
    return 0;
}