HDU 4691 Front compression
Front compression
Time Limit: 5000/5000 MS (Java/Others) Memory Limit: 102400/102400 K (Java/Others)
Total Submission(s): 621 Accepted Submission(s): 255
Total Submission(s): 621 Accepted Submission(s): 255
Problem Description
Front compression is a type of delta encoding compression algorithm whereby common prefixes and their lengths are recorded so that they need not be duplicated. For example:
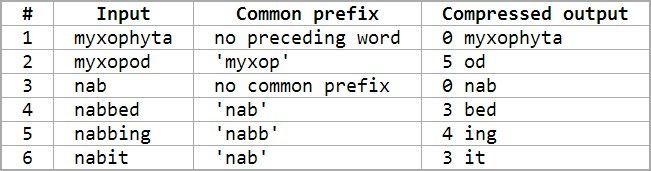
The size of the input is 43 bytes, while the size of the compressed output is 40. Here, every space and newline is also counted as 1 byte.
Given the input, each line of which is a substring of a long string, what are sizes of it and corresponding compressed output?

The size of the input is 43 bytes, while the size of the compressed output is 40. Here, every space and newline is also counted as 1 byte.
Given the input, each line of which is a substring of a long string, what are sizes of it and corresponding compressed output?
Input
There are multiple test cases. Process to the End of File.
The first line of each test case is a long string S made up of lowercase letters, whose length doesn't exceed 100,000. The second line contains a integer 1 ≤ N ≤ 100,000, which is the number of lines in the input. Each of the following N lines contains two integers 0 ≤ A < B ≤ length(S), indicating that that line of the input is substring [A, B) of S.
The first line of each test case is a long string S made up of lowercase letters, whose length doesn't exceed 100,000. The second line contains a integer 1 ≤ N ≤ 100,000, which is the number of lines in the input. Each of the following N lines contains two integers 0 ≤ A < B ≤ length(S), indicating that that line of the input is substring [A, B) of S.
Output
For each test case, output the sizes of the input and corresponding compressed output.
Sample Input
frcode 2 0 6 0 6 unitedstatesofamerica 3 0 6 0 12 0 21 myxophytamyxopodnabnabbednabbingnabit 6 0 9 9 16 16 19 19 25 25 32 32 37
Sample Output
14 12 42 31 43 40
Author
Zejun Wu (watashi)
Source
Recommend
zhuyuanchen520
重新学了一下后缀数组,第一次用后缀数组过题
后缀数组(height[])+RMQ
重新学了一下后缀数组,第一次用后缀数组过题
后缀数组(height[])+RMQ
#include <iostream>
#include <cstring>
#include <cstdio>
#include <cmath>
#define N 100010
#define M 30
using namespace std;
char s1[N];
int sa[N],tsa[N],sum[N],rank[2*N],trank[2*N],height[N];
int dp[N][M];
int main()
{
//freopen("data.in","r",stdin);
void get_sa();
void get_height();
void pre_RMQ();
int get_RMQ(int l,int r);
int digit(int k);
while(scanf("%s",s1)!=EOF)
{
get_sa();
get_height();
pre_RMQ();
int n,x1,y1;
__int64 res1=0,res2=0;
scanf("%d",&n);
for(int i=1;i<=n;i++)
{
int x2,y2;
scanf("%d %d",&x2,&y2);
res1+=(__int64)(y2-x2+1);
if(i==1)
{
res2+=(__int64)(y2-x2+3);
}else
{
int t;
if(x1==x2)
{
t=min(y2-x2,y1-x1);
}else
{
t=get_RMQ(min(rank[x1+1],rank[x2+1])+1,max(rank[x1+1],rank[x2+1]));
if(t+x2<=y2&&t+x1<=y1)
{
;
}else
{
t=min(y2-x2,y1-x1);
}
}
int ans1=digit(t);
int ans2=y2-x2-t+2;
res2+=(__int64)(ans1+ans2);
}
x1 = x2;
y1 = y2;
}
printf("%I64d %I64d\n",res1,res2);
}
return 0;
}
void sorting(int k)
{
memset(sum,0,sizeof(sum));
int l = strlen(s1);
for(int i=1;i<=l;i++)
{
sum[rank[i+k]]++;
}
for(int i=1;i<=l;i++)
{
sum[i]+=sum[i-1];
}
for(int i=l;i>=1;i--)
{
tsa[sum[rank[i+k]]--]=i;
}
memset(sum,0,sizeof(sum));
for(int i=1;i<=l;i++)
{
sum[rank[i]]++;
}
for(int i=1;i<=l;i++)
{
sum[i]+=sum[i-1];
}
for(int i=l;i>=1;i--)
{
sa[sum[rank[tsa[i]]]--]=tsa[i];
}
}
void get_sa()
{
int l = strlen(s1);
memset(rank,0,sizeof(rank));
for(int i=0;i<=l-1;i++)
{
trank[i+1]=s1[i];
}
memset(sum,0,sizeof(sum));
for(int i=1;i<=l;i++)
{
sum[trank[i]]++;
}
for(int i=1;i<=256;i++)
{
sum[i]+=sum[i-1];
}
for(int i=l;i>=1;i--)
{
sa[sum[trank[i]]--]=i;
}
rank[sa[1]]=1;
for(int i=2,p=1;i<=l;i++)
{
if(trank[sa[i]]!=trank[sa[i-1]])
{
p++;
}
rank[sa[i]]=p;
}
for(int i=1;i<=l;i=i*2)
{
sorting(i);
trank[sa[1]]=1;
for(int j=2,p=1;j<=l;j++)
{
if(rank[sa[j]]!=rank[sa[j-1]]||rank[sa[j]+i]!=rank[sa[j-1]+i])
{
p++;
}
trank[sa[j]]=p;
}
for(int j=1;j<=l;j++)
{
rank[j]=trank[j];
}
}
}
void get_height()
{
height[1]=0;
int l = strlen(s1);
for(int i=1,j=0;i<=l;i++)
{
if(rank[i]==1)
{
continue;
}
while(s1[i+j-1]==s1[sa[rank[i]-1]+j-1])
{
j++;
}
height[rank[i]]=j;
if(j>0)
{
j--;
}
}
}
void pre_RMQ()
{
int l = strlen(s1);
for(int i=1;i<=l;i++)
{
dp[i][0]=height[i];
}
for(int j=1;(1<<j)<=l;j++)
{
for(int i=1;i+(1<<(j-1))<=l;i++)
{
dp[i][j]=min(dp[i][j-1],dp[i+(1<<(j-1))][j-1]);
}
}
}
int get_RMQ(int l,int r)
{
int j=0;
while((1<<(j+1))<=(r-l+1))
{
j++;
}
return min(dp[l][j],dp[r-(1<<j)+1][j]);
}
int digit(int k)
{
if(k==0)
{
return 1;
}
int s=0;
while(k!=0)
{
s+=1;
k=k/10;
}
return s;
}