ACM学习历程—NPU1045 2015年陕西省程序设计竞赛网络预赛（热身赛）C题 Graph Theory（递推 && 组合数学 && 大数）

Description

In graph theory, a matching or independent edge set in a graph G = (V , E) is a set of edges ME such that no two edges in the matching M share a common vertex.

The Nobel Prize in XiXiHaHa was awarded to Jerryxf team, amongst other things, their algorithm for finding a matching satisfying certain criteria in a bipartite graph. Since you have also heard that matchings in cycle graphs have applications in chemistry your thoughts centre around a plan for a beautiful future where your Christmas shopping is more luxurious than ever!

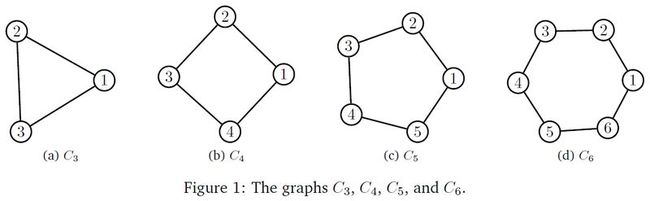
The cycle graph, C_n, n≥3, is a simple undirected graph, on vertex set ｛1,……, n｝, with edge set E(C_n) = {{a , b}  |  |a-b| ≡ 1 mod mod n }. It is 2-regular, and contains n edges. The graphs C₃, C₄, C₅, and C₆ are depicted in Figure 1.

 

Your first step towards Nobel Prize fame is to be able to compute the number of matchings in the cycle graph C_n. In Figure 2 the seven matchings of the graph C₄ are depicted.

 

 

 

 

Figure 2: The matchings of C₄. The edges that are part of the respective matching are coloured green, while the edges left out of the matching are dashed. M₁ =  ,  M₂ = ｛｛2 ,1｝｝ , M₃=｛｛3 , 2｝｝ ,  M₄ =｛｛4 , 3｝｝, M₅ = ｛｛1 , 4｝｝, M₆ = ｛｛2 , 1｝,｛4 , 3｝｝, and M₇ = ｛｛3 , 2｝,｛1 , 4｝｝

 

Input

For each test case, you get a single line containing one positive integer: n, with 3≤n≤10000.

Output

For each test case, a row containing the number of matchings in C_n.

Sample Input

3
4
100

Sample Output

4
7
792070839848372253127

 

题目意思就是在一个环上放线段，线段不能相邻，求放法数。

这是一个典型的组合类型问题，不过圆形的排列不太好搞。

我们考虑直链型的：对于直链型的，不妨设f(n)表示以n结尾的直链型的方法数。

考虑n处不放线段，那么去掉n，剩下(n-1)个就变成了子问题f(n-1)；

考虑n处放线段，那么n-1处必然不能放，于是剩下的(n-2)个就变成了子问题f(n-2)；

于是对于直链的：f(n) = f(n-1) + f(n-2)，正好是一个费波拉契数列。

 

于是对于圆形排列的就好考虑了：不妨设s(n)表示n个的圆形排列的数目。

考虑第n个不放线段，那么剩余的(n-1)变可以从第n个那处展开成直链的f(n-1);

考虑第n个放线段，那么第1个和第n-1个必然不能放，那么剩下n-3个便是直链的f(n-3)

于是s(n) = f(n-1) + f(n-3)，理论上到此处变可以求s(n)了，首先对f(n)将前10000项打表，然后就可以求任意s(n)（注意f(0) = 1, f(1) = 2）

 

不过由于s(n) = f(n-1) + f(n-3)， 自然s(n) = s(n-1) + s(n-2)，其本身也是费波拉契数列。

 

由于此处需要考虑大数，故采用了Java的大数类。

 

代码：

import java.math.BigInteger;
import java.util.Scanner;

public class Main
{
    public static void main(String args[])
    {
        BigInteger f[] = new BigInteger[10001];
        f[0] = new BigInteger("1");
        f[1] = new BigInteger("2");
        for (int i = 2; i <= 10000; ++i)
        {
            f[i] = new BigInteger("0");
            f[i] = f[i-1].add(f[i-2]);
        }
        Scanner input = new Scanner(System.in);
        int n;
        while (input.hasNext())
        {
            n = input.nextInt();
            System.out.println(f[n-1].add(f[n-3]));
        }
    }
}