环状一维数组

结对伙伴：郭婷 朱慧敏

1.题目:返回一个整数数组中最大子数组的和。

要求：

输入一个整形数组，数组里有正数也有负数。

数组中连续的一个或多个整数组成一个子数组，每个子数组都有一个和。

如果数组A[0]……A[j-1]首尾相邻，允许A[i-1]， …… A[n-1]， A[0]……A[j-1]之和最大。

同时返回最大子数组的位置。

求所有子数组的和的最大值。要求时间复杂度为O(n)。

2.设计思路

开始我们是想在原来程序的基础上将数组进行扩展，对于一个n的一维数组，如果成环可以将数组长度扩展为2*n-1的。

3.源代码

#include<iostream>

#include<cmath>

using namespace std;

#define N 1000

#define max(a,b)(a>b?a:b)



int MaxSum_base(int arr[], int n)

{

    int i, sum = 0;

    int max = arr[0];

    for (i = 0; i<n; i++)

    {

        if (sum <= 0)

        {

            sum = arr[i];

        }

        else

        {

            sum = sum + arr[i];

        }

        if (sum>max)

        {

            max = sum;

        }

    }

    return max;



}



int MaxSum_linked(int arr[], int n)

{

    int c = arr[0];

    int ans = c;

    bool h = false;

    for (int i = 1; i < n * 2 - 1; i++)

    {

        if (i < n&&arr[i] < 0)

            h = true;

        c = max(c + arr[i%n], arr[i%n]);

        ans = max(ans, c);

        if (i == n - 1 && !h)

            return ans;

    }

    return ans;

}



void MaxSum_location(int * arr, int n, int & start,int &end)

{

    int maxSum = -N;

    int sum = 0;

    int cstart = start = 0;  //cstart记录每次当前起始位置 

    for (int i = 0; i < n; ++i)

    {

        if (sum < 0)

        {

            sum = arr[i];

            cstart = i;     // 记录当前的起始位置

        }

        else

        {

            sum += arr[i];

        }

        if (sum > maxSum)

        {

            maxSum = sum;

            start = cstart; // 记录并更新最大子数组起始位置

            end = i;

        }

    }

}





int main()

{

    int i=0, n, a[100],s,e;

    cout << "输入数组个数：";

    cin >> n;

    cout << "请输入数组：";

    for (i = 0; i < n; i++)

    {

       cin >> a[i];

    }

    int x = MaxSum_base(a, n);

    cout << ">>线性最大子数组的和为：" << x << endl;

    int sum = MaxSum_linked(a, n);

    cout << ">>环形最大子数组的和为：" <<sum<< endl;

    MaxSum_location(a,n,s,e);

    cout << "最大子数组的位置是：" <<"第"<< s+1<<"个到第"<< e << "个" <<endl;



}

4.程序截图

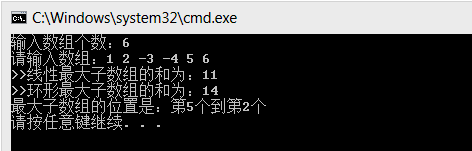
5.总结

在程序实现后，我们以为完成了，可是后来发现有些结果不对。有些数组成环后子数组的长度会超过数组本身的长度，这就不对了，于是我们有进一步修改了程序。这次的程序我们发现原来程序本身也会隐藏一些错误，需要我们对每一种情况进行分析，解决。