2013蓝桥杯初赛c语言专科组--题目与答案
1. 题目标题: 猜年龄 美国数学家维纳(N.Wiener)智力早熟,11岁就上了大学。他曾在1935~1936年应邀来中国清华大学讲学。 一次,他参加某个重要会议,年轻的脸孔引人注目。于是有人询问他的年龄,他回答说: “我年龄的立方是个4位数。我年龄的4次方是个6位数。这10个数字正好包含了从0到9这10个数字,每个都恰好出现1次。” 请你推算一下,他当时到底有多年轻。 通过浏览器,直接提交他那时的年龄数字。 注意:不要提交解答过程,或其它的说明文字。
答案:18
2. 标题: 马虎的算式 小明是个急性子,上小学的时候经常把老师写在黑板上的题目抄错了。 有一次,老师出的题目是:36 x 495 = ? 他却给抄成了:396 x 45 = ? 但结果却很戏剧性,他的答案竟然是对的!! 因为 36 * 495 = 396 * 45 = 17820 类似这样的巧合情况可能还有很多,比如:27 * 594 = 297 * 54 假设 a b c d e 代表1~9不同的5个数字(注意是各不相同的数字,且不含0) 能满足形如: ab * cde = adb * ce 这样的算式一共有多少种呢? 请你利用计算机的优势寻找所有的可能,并回答不同算式的种类数。 满足乘法交换律的算式计为不同的种类,所以答案肯定是个偶数。 答案直接通过浏览器提交。 注意:只提交一个表示最终统计种类数的数字,不要提交解答过程或其它多余的内容。
答案:142
3. 标题: 振兴中华
小明参加了学校的趣味运动会,其中的一个项目是:跳格子。
地上画着一些格子,每个格子里写一个字,如下所示:(也可参见p1.jpg)
从我做起振
我做起振兴
做起振兴中
起振兴中华
比赛时,先站在左上角的写着“从”字的格子里,可以横向或纵向跳到相邻的格子里,但不能跳到对角的格子或其它位置。一直要跳到“华”字结束。
要求跳过的路线刚好构成“从我做起振兴中华”这句话。
请你帮助小明算一算他一共有多少种可能的跳跃路线呢?
答案是一个整数,请通过浏览器直接提交该数字。
答案:35
4. 标题: 幻方填空 幻方是把一些数字填写在方阵中,使得行、列、两条对角线的数字之和都相等。 欧洲最著名的幻方是德国数学家、画家迪勒创作的版画《忧郁》中给出的一个4阶幻方。 他把1,2,3,...16 这16个数字填写在4 x 4的方格中。 如图p1.jpg所示,即: 16 ? ? 13 ? ? 11 ? 9 ? ? * ? 15 ? 1 表中有些数字已经显露出来,还有些用?和*代替。 请你计算出? 和 * 所代表的数字。并把 * 所代表的数字作为本题答案提交。 答案是一个整数,请通过浏览器直接提交该数字。 答案:12
5. 题目标题:公约数公倍数 我们经常会用到求两个整数的最大公约数和最小公倍数的功能。 下面的程序给出了一种算法。 函数 myfunc 接受两个正整数a,b 经过运算后打印出 它们的最大公约数和最小公倍数。 此时,调用 myfunc(15,20) 将会输出: 3 60 // 交换数值 void swap(int *a,int *b) { int temp; temp=*a; *a=*b; *b=temp; } void myfunc(int a, int b) { int m,n,r; if(a<b) swap(&a,&b); m=a;n=b;r=a%b; while(r!=0) { a=b;b=r; r=a%b; } printf("%d\n",b); // 最大公约数 printf("%d\n", ____________________________________); // 最小公倍数 } 请分析代码逻辑,并推测划线处的代码,通过网页提交。 答案: m*n/b
标题:三部排序 一般的排序有许多经典算法,如快速排序、希尔排序等。 但实际应用时,经常会或多或少有一些特殊的要求。我们没必要套用那些经典算法,可以根据实际情况建立更好的解法。 比如,对一个整型数组中的数字进行分类排序: 使得负数都靠左端,正数都靠右端,0在中部。注意问题的特点是:负数区域和正数区域内并不要求有序。可以利用这个特点通过1次线性扫描就结束战斗!! 以下的程序实现了该目标。 其中x指向待排序的整型数组,len是数组的长度。 void sort3p(int* x, int len) { int p = 0; int left = 0; int right = len-1; while(p<=right){ if(x[p]<0){ int t = x[left]; x[left] = x[p]; x[p] = t; left++; p++; } else if(x[p]>0){ int t = x[right]; x[right] = x[p]; x[p] = t; right--; } else{ __________________________; //填空位置 } } } 如果给定数组: 25,18,-2,0,16,-5,33,21,0,19,-16,25,-3,0 则排序后为: -3,-2,-16,-5,0,0,0,21,19,33,25,16,18,25 请分析代码逻辑,并推测划线处的代码,通过网页提交 答案:p++
7. 标题:核桃的数量 小张是软件项目经理,他带领3个开发组。工期紧,今天都在加班呢。为鼓舞士气,小张打算给每个组发一袋核桃(据传言能补脑)。他的要求是: 1. 各组的核桃数量必须相同 2. 各组内必须能平分核桃(当然是不能打碎的) 3. 尽量提供满足1,2条件的最小数量(节约闹革命嘛) 程序从标准输入读入: a b c a,b,c都是正整数,表示每个组正在加班的人数,用空格分开(a,b,c<30) 程序输出: 一个正整数,表示每袋核桃的数量。 例如: 用户输入: 2 4 5 程序输出: 20 再例如: 用户输入: 3 1 1 程序输出: 3
#include <stdio.h> void swap(int *a, int *b) { int temp; temp = *a; *a = *b; *b = temp; } int f(int a, int b) { int m, n, r; if (a<b) swap(&a, &b); m = a, n = b, r = a % b; while (r != 0) { a = b; b = r; r = a % b; } return m * n / b; } int main() { int a, b, c; scanf("%d %d %d", &a, &b, &c); printf("%d", f(f(a,b), f(b,c))); return 0; }
8. 题目标题:打印十字图 小明为某机构设计了一个十字型的徽标(并非红十字会啊),如下所示(可参见p1.jpg) $$$$$$$$$$$$$ $ $ $$$ $$$$$$$$$ $$$ $ $ $ $ $ $$$ $$$$$ $$$ $ $ $ $ $ $ $ $ $ $$$ $ $$$ $ $ $ $ $ $ $ $ $ $ $ $ $$$$$ $ $ $ $ $ $ $ $ $ $ $ $ $$$ $ $$$ $ $ $ $ $ $ $ $ $ $$$ $$$$$ $$$ $ $ $ $ $ $$$ $$$$$$$$$ $$$ $ $ $$$$$$$$$$$$$ 对方同时也需要在电脑dos窗口中以字符的形式输出该标志,并能任意控制层数。 为了能准确比对空白的数量,程序要求对行中的空白以句点(.)代替。 输入格式: 一个正整数 n (n<30) 表示要求打印图形的层数 输出: 对应包围层数的该标志。 例如: 用户输入: 1 程序应该输出: ..$$$$$.. ..$...$.. $$$.$.$$$ $...$...$ $.$$$$$.$ $...$...$ $$$.$.$$$ ..$...$.. ..$$$$$.. 再例如: 用户输入: 3 程序应该输出: ..$$$$$$$$$$$$$.. ..$...........$.. $$$.$$$$$$$$$.$$$ $...$.......$...$ $.$$$.$$$$$.$$$.$ $.$...$...$...$.$ $.$.$$$.$.$$$.$.$ $.$.$...$...$.$.$ $.$.$.$$$$$.$.$.$ $.$.$...$...$.$.$ $.$.$$$.$.$$$.$.$ $.$...$...$...$.$ $.$$$.$$$$$.$$$.$ $...$.......$...$ $$$.$$$$$$$$$.$$$ ..$...........$.. ..$$$$$$$$$$$$$.. 请仔细观察样例,尤其要注意句点的数量和输出位置。
#include <stdio.h> void swap(int *a, int *b) { int temp; temp = *a; *a = *b; *b = temp; } int go(int i, int j, int n) { if (i > n * 2 + 3) i = n * 4 + 6 - i; if (j > n * 2 + 3) j = n * 4 + 6 - j; if (i < j) swap(&i, &j); if (i <= 2 && j <= 2) return 0; if (i % 2 == 1 && j >= i - 2) return 1; if (j % 2 == 1 && j != i - 1) return 1; return 0; } int main() { int n; scanf("%d", &n); int i, j; for (i = 1; i <= n*4+5; i++) { for (j = 1; j <= n*4+5; j++) { if (go(i, j, n)) printf("$"); else printf("."); } printf("\n"); } return 0; }
9. 标题:带分数 100 可以表示为带分数的形式:100 = 3 + 69258 / 714 还可以表示为:100 = 82 + 3546 / 197 注意特征:带分数中,数字1~9分别出现且只出现一次(不包含0)。 类似这样的带分数,100 有 11 种表示法。 题目要求: 从标准输入读入一个正整数N (N<1000*1000) 程序输出该数字用数码1~9不重复不遗漏地组成带分数表示的全部种数。 注意:不要求输出每个表示,只统计有多少表示法! 例如: 用户输入: 100 程序输出: 11 再例如: 用户输入: 105 程序输出: 6
#include <stdio.h> #define N 9 int num[N] = {1,2,3,4,5,6,7,8,9}; int tag[3][3] = {{4,3,2},{5,3,1},{6,2,1}}; void swap(int *a, int *b) { int temp; temp = *a; *a = *b; *b = temp; } int go(int i, int n) { int a, b, c; int count = 0; for (a = 0; a < 3; a++) { int r[3] = {0} , d = 0; for (b = 0; b < 3; b++) for (c = 0; c < tag[a][b]; c++) r[b] = r[b] * 10 + num[d++]; if (r[0] + r[1] / r[2] == n && r[1] % r[2] == 0) count++; if (r[0] + r[2] / r[1] == n && r[2] % r[1] == 0) count++; if (r[1] + r[0] / r[2] == n && r[0] % r[2] == 0) count++; if (r[1] + r[2] / r[0] == n && r[2] % r[0] == 0) count++; if (r[2] + r[0] / r[1] == n && r[0] % r[1] == 0) count++; if (r[2] + r[1] / r[0] == n && r[1] % r[0] == 0) count++; } while (i < N) { int k = i + 1; while (k < N) { swap(num + i, num + k); count += go(i + 1, n); swap(num + i, num + k); k++; } i++; } return count; } int main() { int n; scanf("%d", &n); printf("%d", go(0, n)); return 0; }
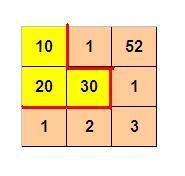
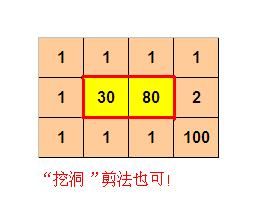
10. 标题:剪格子 如图p1.jpg所示,3 x 3 的格子中填写了一些整数。 我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是60。 本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。 如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。 如果无法分割,则输出 0 程序输入输出格式要求: 程序先读入两个整数 m n 用空格分割 (m,n<10) 表示表格的宽度和高度 接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000 程序输出:在所有解中,包含左上角的分割区可能包含的最小的格子数目。 例如: 用户输入: 3 3 10 1 52 20 30 1 1 2 3 则程序输出: 3 再例如: 用户输入: 4 3 1 1 1 1 1 30 80 2 1 1 1 100 则程序输出: 10
#include <stdio.h> #define N 10 int num[N][N]; // tag是用来标志 格子有没有加入,用颜色来表示,1为已加入,黑色, 0为没加入,白色 // 初始化全为白色 int tag[N][N] = {0}; int m, n; int r = 100; //判断格子(i,j)颜色是否t,一样的话就找他周围颜色也为t //返回找到的总数 int find(int i, int j, int t, int ntag[][N]) { int count = 0; //出界或走过 if (i < 0 || i >= n || j < 0 || j >= m || ntag[i][j] == 1) return 0; //标为已走过 ntag[i][j] = 1; //颜色不一样,返回 if (tag[i][j] != t) return 0; count++; count += find(i - 1, j, t, ntag); count += find(i + 1, j, t, ntag); count += find(i, j - 1, t, ntag); count += find(i, j + 1, t, ntag); return count; } //判断是否当前的tag,能不能剪成两块 int isbad() { int i, j, k = 0; int t = tag[0][0]; int ntag1[N][N] = {0}; int ntag2[N][N] = {0}; //找一块连在一起的黑格子 int ge1 = find(0, 0, t, ntag1); for (i = 0; i < n; i++) { for (j = 0; j < m; j++) { if (tag[i][j] != t) { k = 1; break; } } if (k == 1) break; } if (i == n && j == m) return 0; //找连在一起的白格子 int ge2 = find(i, j, tag[i][j], ntag2); return ge1 + ge2 != m * n; //若黑+白 != 总数 说明不止两块,如:黑$白# /* ##$$# #$$## 这种情况就有2块白的,1块黑的 */ } // 判断格子(i,j)是否出界,以及判断格子可不可以剪成两块连续的格子 int bad(int i, int j) { if (i < 0 || i >= n || j < 0 || j >= m || tag[i][j] == 1) return 1; tag[i][j] = 1; //格子加入 int b = isbad(); //判断格子可不可以剪成两块连续的格子 tag[i][j] = 0; //格子退出 return b; } /* * i, j 下一个要加入的格子 * k 已加入的格子数 * count 剩余总分 * 执行完,全局tag是没有改变的 */ void go(int i, int j, int k, int count) { // 判断格子是否可加入 if (bad(i, j) || count < num[i][j]) return; // 格子可加入,已加入格子数+1 k++; // 如果剩余总分刚好等于加入的格子的分数,那么这种情况符合要求 if (count == num[i][j]) { if (r > k) r = k; return; } // 加入格子,tag改变为1 tag[i][j] = 1; count -= num[i][j]; // 寻找周围格子是否可加入 go(i - 1, j, k, count); // 执行完,tag是没有改变的 go(i + 1, j, k, count); // 执行完,tag是没有改变的 go(i, j - 1, k, count); // 执行完,tag是没有改变的 go(i, j + 1, k, count); // 执行完,tag是没有改变的 // 格子退出, tag恢复为0,也就是保证 执行完,tag是没有改变的 tag[i][j] = 0; } int main() { scanf("%d %d", &m, &n); int i, j; int half = 0; for (i = 0; i < n; i++) for (j = 0; j < m; j++) { scanf("%d", &num[i][j]); // 计算总分 half += num[i][j]; } // 判断总分是否为偶数 if (half % 2 == 0 && half >= num[0][0] * 2) { // 计算总分的一半 half /= 2; // go(int i, int j, int k, int count) // 下一个要加入的格子为 i, j: (0,0) // 已加入的格子数为0 // half 剩余总分 go(0, 0, 0, half); } if (r == 100) r = 0; printf("%d", r); return 0; }
以上是个人的答案,不知道有没有问题,欢迎指正。。。