cdoj 414 八数码 （双广+康拓展开）

 一道关乎人生完整的问题。

DBFS的优越：避免了结点膨胀太多。

假设一个状态结点可以扩展m个子结点，为了简单起见，假设每个结点的扩展都是相互独立的。

分析：起始状态结点数为1，每加深一层，结点数An = An-1*m。假如搜索了i层找到终点，那么经过的结点数是O(i^m)，如果从两边同时搜索，结点数是O(i^(m/2))。

极端情况，终点完全封闭。

 

 

DBFS的正确姿势：

图片来源：http://www.cppblog.com/Yuan/archive/2011/02/23/140553.aspx

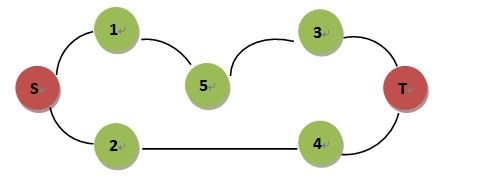
下面是原博客上的分析：

交替结点可能会因为扩展顺序而认为s-1-5-3-t是最短路。//这也可能得到正确结果，与结点的扩展顺序有关系

然而交替层次的做法才是正确的。

优化：提供速度的关键在于使状态扩展得少一些，所以优先选择队列长度较少的去扩展，保持两边队列长度平衡。这比较适合于两边的扩展情况不同时，一边扩展得快，一边扩展得慢。如果两边扩展情况一样时，加了后效果不大，不过加了也没事。

 

 ----------------------------------分割线------------------------------------------------------

DBFS的代码也是磕了好久想到怎么实现的。

加了奇偶剪枝和一些小优化

 

更新。经过仔细思考，简化了代码。

/*

 Created by Rey Chen on 2015.7.5

 */



#include<bits/stdc++.h>

using namespace std;



//#define local

const int maxn = 362880;

int vis1[maxn];

int vis2[maxn];//保存距离起点的距离，初始值-1

int fac[9];



struct node

{

    int e[9];

    int p;

    int cod;//避免二次计算，初始值为-1

    int code() {

        if(~cod) return cod;

        int Hash = 0;

        for(int i = 0; i < 9; i++) {

            int cnt = 0;

            for(int j = i+1; j < 9; j++)

                if(e[j] < e[i]) cnt++;

            Hash += fac[8-i] * cnt;

        }

        return cod = Hash;

    }

    int rev_value(){//用于奇偶剪枝

        int res = 0, cnt ,i ,j;

        for(i = 0; i < 9; i++) {

            if(e[i]) {

                cnt = 0;

                for(j = i+1; j < 9; j++)

                    if(e[j] && e[j] < e[i]) cnt++;

                res += cnt;

            }

        }

        return res;

    }

};



node start;

node ed;

int edHash;

int nodesz;

typedef vector<node>* vnodep;

vector<node> v1;

vector<node> v2;

vector<node> v3;

vector<node>:: iterator it,tmp_it;



const int dx[] = {-1, 1, 0, 0};

const int dy[] = { 0, 0,-1, 1};

bool ilegal[9][4];

void solve()

{

    if(start.rev_value()&1) { puts("unsolvable"); return; }//忽略0，操作不会改变逆序数总数的奇偶性。

    int t;

    t = start.code();

    if(t == edHash) { puts("0");return;}

    memset(vis1,-1,sizeof(vis1) );

    memset(vis2,-1,sizeof(vis2) );

    vis1[t] = 0;

    vis2[edHash] = 0;



    v1.clear(); v2.clear(); v3.clear();

    vnodep q1 = &v1, q2 = &v2, nxt = &v3;

    q1->push_back(start);

    q2->push_back(ed);

    int *V1 = vis1, *V2 = vis2;

    while( !q1->empty() && !q2->empty() ) {

        if(q1->size() > q2->size()) swap(q1,q2),swap(V1,V2); //化简代码的小技巧

        for(it = q1->begin(), tmp_it = q1->end(); it != tmp_it ; it++){

            node& u = *it;

            node v;

            for(int i = 0;i < 4;i++){

                if(ilegal[u.p][i]) continue;

                int np = u.p + dx[i]*3 + dy[i];

                memcpy(&v,&u,nodesz); v.cod = -1;//memcpy 比直接赋值要快

                swap(v.e[np],v.e[u.p]);

                if(!~V1[t = v.code()]){

                    V1[t] = V1[u.code()] + 1;

                    if(~V2[t]){  printf("%d\n",V2[t]+V1[t]);  return;  }

                    v.p = np;

                    nxt->push_back(v);

                }

            }

        }

        q1->clear();

        swap(q1,nxt);

    }

    puts("unsolvable");

}



void init(){

    fac[0] = 1;

    for(int i = 1; i < 9; i++)

        fac[i] = fac[i-1]*i;

     for(int i = 0; i < 3; i++)

     for(int j = 0; j < 3; j++){

        for(int k = 0; k < 4; k++)

            if( (i == 0&& k == 0) || (i == 2&& k == 1) || (j == 0&& k == 2) || (j == 2&& k == 3) )

                ilegal[i*3+j][k] = true;

            else ilegal[i*3+j][k] = false;

     }

}



int main()

{

#ifdef local

    freopen("in.txt","r",stdin);

    freopen("out.txt","w",stdout);

#endif // local

    char ch,s[24];

    init();

    for(int i = 0; i < 8;i ++)

        ed.e[i] = i+1;

    ed.e[8] = 0;

    ed.p = 8;

    ed.cod = -1;

    edHash = ed.code();

    nodesz = sizeof(ed);





    while(gets(s)) {

        int j = 0;

        for(int i = 0; i < 9; i ++, j++) {

            while(sscanf(s+j,"%c",&ch),ch == ' ')j++;

            if(ch == 'x'){

                start.e[i] = 0; start.p = i;

            }else {

                start.e[i] = ch - '0';

            }

        }

        start.cod = -1;

        solve();

    }

    return 0;

}

View Code

 花了点时间写了A*。A*的关键在于估价函数，估价函数必须要小于实际值，越接近越好。

这里取的是除去x以后的曼哈顿距离。

这题为什么不需要两个表？需要open表是因为有可能有捷径的出现，这题不需要。

#include<bits/stdc++.h>

using namespace std;



int t[9],s[9],Zero,tHashCode;

int fac[9];

struct node

{

    int p[9], z, f, dist, hashCode;

    bool operator < (const node& rhs) const {

       return f > rhs.f || (f == rhs.f && dist > rhs.dist);

    }

};



inline int Hash(int *a)

{

    int ans = 0;

    for(int i = 0; i < 8; i++) {

        int cnt = 0;

        for(int j = i+1; j < 9; j++) if(a[j] < a[i]) cnt++;

        ans += fac[8-i] * cnt;

    }

    return ans;

}



inline int Rev_value(int *a){

    int ans = 0;

    for(int i = 0; i < 8; i++) {

        int cnt = 0;

        for(int j = i+1; j < 9; j++) if(a[j] && a[j] < a[i]) cnt++;

        ans += cnt;

    }

    return ans;

}

int Cost[9][9];



//除去x之外到目标的网格距离和

//x 和 其他数交换，理想情况每次距离减一

inline void Manhattan(node &A)

{

   A.f = A.dist;

    for(int i = 0; i < 9; i++)if(A.p[i])

        A.f += Cost[i][A.p[i]-1];

}



bool vis[362880];

const int dx[] = {-1, 1, 0, 0};

const int dy[] = { 0, 0,-1, 1};

int dz[9];

bool ilegal[9][4];



void AstarBfs()

{

    if(Rev_value(s)&1) { puts("unsolvable"); return; }

    node u;

    u.hashCode = Hash(s);

    if(u.hashCode == tHashCode) {puts("0"); return;}

    memset(vis,0,sizeof(vis));

    vis[u.hashCode] = 1;

    memcpy(u.p,s,sizeof(s));

    u.dist = 0;

    u.z = Zero;

    priority_queue<node> q;

    Manhattan(u);

    q.push(u);

    while(q.size()) {

        u = q.top(); q.pop();

        if(u.hashCode == tHashCode) {printf("%d\n",u.dist);return;}

        node v;

        for(int i = 0; i < 4; i++) {

            if(ilegal[u.z][i]) continue;

            v.z = u.z + dz[i];

            memcpy(v.p,u.p,sizeof(u.p));

            swap(v.p[v.z],v.p[u.z]);

            v.hashCode = Hash(v.p);

            if(vis[v.hashCode]) continue;

            vis[v.hashCode] = 1;

            v.dist = u.dist +1;

            Manhattan(v);

            q.push(v);

        }

    }

  puts("unsolvable");

}



void init()

{

    for(int i = 0; i < 9; i++)

        for(int j = 0; j < 9; j++)

        Cost[i][j] = (abs(i/3-j/3) + abs(i%3-j%3));

    for(int i = 0; i < 8; i++)

        t[i] = i+1;

    t[8] = 0;

    fac[0] = 1;

    for(int i = 1; i < 9; i++)

        fac[i] = fac[i-1]*i;

    tHashCode = Hash(t);

    for(int i = 0; i < 3; i++)

    for(int j = 0; j < 3; j++)

        for(int k = 0; k < 4; k++){

            int nx = i+dx[k], ny = j + dy[k];

            ilegal[i*3+j][k] = !(nx>=0 && nx < 3 && ny >= 0 && ny < 3);

        }

    for(int k = 0; k < 4; k++) dz[k] = dx[k]*3 + dy[k];

}





int main()

{

    init();

    char str[20];

    while(fgets(str,20,stdin)) {

        int j = 0;

        for(int i = 0; i < 9; i++, j++){

            char ch;

            while(sscanf(str+j,"%c",&ch),ch == ' ')j++;

            if(ch == 'x'){

                s[i] = 0;Zero = i;

            }else {

                s[i] = ch - '0';

            }

        }

        AstarBfs();

    }

    return 0;

}

View Code

 

附上数据生成器

#include<bits/stdc++.h>

using namespace std;



int main()

{

    srand( time( NULL ) );

    char s[20] ;

    char ori[20] = "12345678";

    int n = 10;

    int m = 10;

    int init = 1;

    for(int i = 0; i < 50; i++) next_permutation(ori,ori+8);

        for(int i=0;i<n;i++)

        {

            for(int j = 0;j<m;j++){

                strcpy(s,ori);

                s[8] = 'x';s[9] = '\0';

                swap(s[8],s[rand()%8]);

                for(int k = 0;k < 9; k++)

                    printf("%c%c",s[k],k==8?'\n':' ');

            }

            next_permutation(ori,ori+8);

        }



}

View Code

.bat

:loop

make.exe>data.txt

std.exe<data.txt>std.txt

my<data.txt>my.txt

fc my.txt std.txt

if not errorlevel 1 goto loop

pause