数据结构学习笔记4.4--删除节点
删除节点是二叉搜索树比较比较复杂的,一般删除节点有三种情况:
1.删除节点是叶子节点(没有字节点)。
2.删除节点只有一个子节点。
3.删除节点有两个子节点。
第一种是情况是最简单的;第二种情况也比较简单;第三种情况是最复杂的。
在真正删除节点前,还需要执行步骤:查找删除的节点
代码如下:
Node current = root; // 当前节点 Node parent = root; // 父节点,用于标记删除节点的父节点 boolean isLeftChild = true; // 是否是左子节点 // 查找要删除的节点 while (current.iData != key) { // 保存父节点的引用 parent = current; // 删除节点在左子树 if (key < current.iData) { isLeftChild = true; current = current.leftChild; } // 删除节点在左子树 else { isLeftChild = false; current = current.rightChild; } // 找不到删除节点,返回 if (current == null) { return false; } }
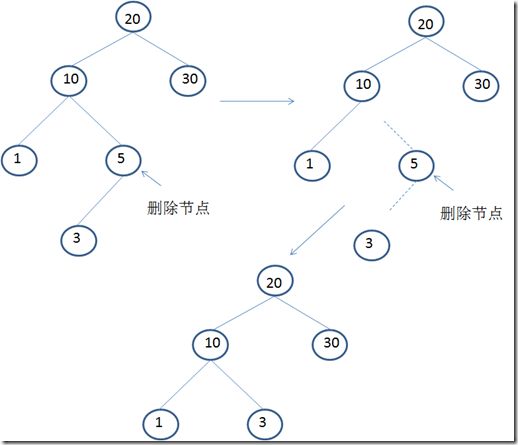
1.删除节点是叶子节点,即删除没有子节点的节点。
删除叶子节点,只要改变该节点的父节点的引用,将其置为null就可以了。
此时删除节点已经不再是树的组成部分,由java垃圾回收机制处理,而不需要做任何操作。
需要删除的节点是“5”,此时该删除节点后,将与其父节点(10)的引用断开。这样,“5”就与整棵树剥离关系,节点“10”的右子节点引用为null。
代码:
// 删除没有子节点的节点 // 即删除节点为current,此时其左子节点、右子节点的应用都为null if (current.leftChild == null && current.rightChild == null) { if (current == root) { root = null; } else if (isLeftChild) { // 修改current父节点左子节点的引用 parent.leftChild = null; } else { // 修改current父节点右子节点的引用 parent.rightChild = null; } }
在找到要删除的节点current后,首先要判断它是不是为根节点,如果为根节点,则设置为null,这样整棵树都被清空;否则,将current的父节点了leftChild或者rightChild置为null。
2.删除节点只有一个字节点
这种情况稍微比第一种复杂,因为删除节点多了一个子节点(只能有一个节点,要么是左子节点,要么是右子节点)。
这样,在删除掉该节点后,需要将删除节点的子节点“连接”到删除节点的父节点上(实际上引用变化),
具体引用变化为:删除节点子节点的引用 赋值给 删除节点父节点的引用,这样父节点就指向正确的字节点。
要删除节点“5”(该节点有左子节点“3”),删除该节点后,断开该节点与父节点“10”的连接,
将删除节点“5”左子节点的引用(指向“3”)赋值给”5”的父节点”10”右子节点的,这样,”10”就指向了”3”,即”10”的右子节点为”3”。
代码:
// 删除节点current的右子节点为空,即只有左子节点 else if (current.rightChild == null) { // 判断是否为根 if (current == root) { root = current.leftChild; } // 如果删除节点为parent的左子节点,则引用赋值为左子树 else if (isLeftChild) { parent.leftChild = current.leftChild; } // 如果删除节点为parent的右子节点,则引用赋值为右子树 else { parent.rightChild = current.leftChild; } } // 删除节点current的左子节点为空,即只有右子节点 else if (current.leftChild == null) { // 判断是否为根 if (current == root) { root = current.rightChild; } // 如果删除节点为parent的左子节点,则引用赋值为左子树 else if (isLeftChild) { parent.leftChild = current.rightChild; } // 如果删除节点为parent的右子节点,则引用赋值为右子树 else { parent.rightChild = current.rightChild; } }
实际上,在删除节点的左子节点(或右子节点)有可能是一个子树,在赋值给父节点引用操作中,可以理解为:整棵子树上移,这样便于记忆。
3.删除节点有两个子节点
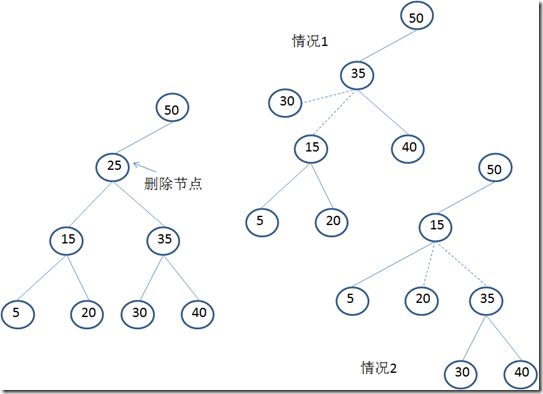
删除节点有两个字节点,这样的情况就复杂了。因为不能按照上面的思路,用它的一个字节点代替它。比如:
在删除节点“25”的时候,出现了两种情况,按照前面的思路,如果用字节点替换,右子节点替换(情况1)与左子节点替换(情况2)都会多出一个节点(分别是30和20),
这两个节点放在哪里都不合适,但是又不能删掉它,所以用字节点替换的思路是行不通的。
解决办法:寻找删除节点的后继。
由于二叉搜索树是是按照关键字的升序排列的,因此比删除节点次高的节点就是该节点的后继。
查找方法,有两种情形。
(1)删除节点的右子节点没有左子节点,此时这个右子节点就是后继。
(2)删除节点的右子节点有左子节点,定位到这个左子节点,然后找这个左子节点在左子节点,依次寻找下去,最后一个左子节点就是删除节点的后继。
记忆方法:按照中序遍历投影法,找到删除节点,往后推一个节点,就是它的后继。
代码:
// 找到后继 Node successor = getSuccessor(current); // 判断删除节点是否为根的情形 if (current == root) { root = successor; } else if (isLeftChild) { // 连接删除节点的父节点与后继节点 parent.leftChild = successor; } else { // 连接删除节点的父节点与后继节点 parent.rightChild = successor; } successor.leftChild = current.leftChild; } /** * 获取后继节点 * @param delNode 删除节点 * @return 后继节点 */ private Node getSuccessor(Node delNode) { Node successorParent = delNode; // 存放后继节点的父节点,因为需要断开后继节点,需要保存父节点的引用 Node successor = delNode; // 存放后继节点 Node current = delNode.rightChild; // 当前节点 // 循环查找后继节点,最后currnt一定为null while (current != null) { successorParent = successor; successor = current; current = current.leftChild; } // 后继节点不是右子节点,即沿着左子节点路径寻找的情形 if (successor != delNode.rightChild) { // 将后继节点的右子节点(有可能是右子树)的引用赋值给后继的父节点,即连接父节点与孙节点 // 这样才能将后继节点断开,同时保持后继节点的子节点关系 successorParent.leftChild = successor.rightChild; // 将删除节点的右子节点引用赋值给后继节点 // 由于后继替换到删除节点的位置,因此需要改变删除节点右子节点的连接关系 successor.rightChild = delNode.rightChild; } return successor; }
这里对以下四个步骤图解说明:
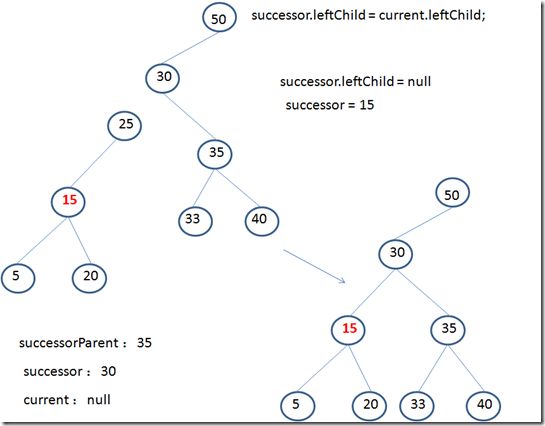
(1)successorParent.leftChild = successor.rightChild;
(2)successor.rightChild = delNode.rightChild;
(3)parent.leftChild = successor; (或parent.rightChild = successor; )
(4)successor.leftChild = current.leftChild;
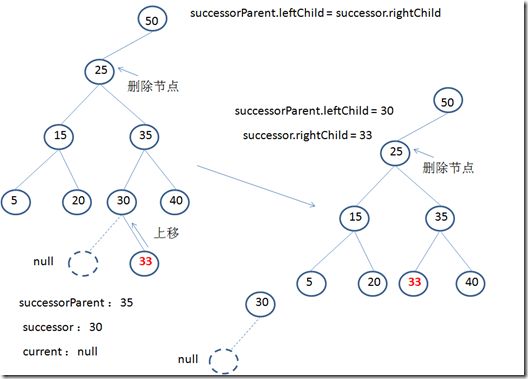
1.successorParent.leftChild = successor.rightChild;
这一步作用是:连接 后继父节点与后继右子节点。
可以看到,实际上是将successor的右子节点(有可能是右子树,这里没有画出来)上移,连接successorParent。
同时,successorParent.leftChild实际上就是successor。
2.successor.rightChild = delNode.rightChild;
这一步作用是:连接 后继与删除节点右子节点。
看到经过删除节点是“25”,因为这个节点要被删除掉,就不再是树的一部分。
这样删除节点“25”的右子节点(可能包含子树)需要与30连接起来,因此,这行代码就是这个作用。
同时我们也看到,此时形成了两棵树,后继“30”并没有与整个树关联起来。
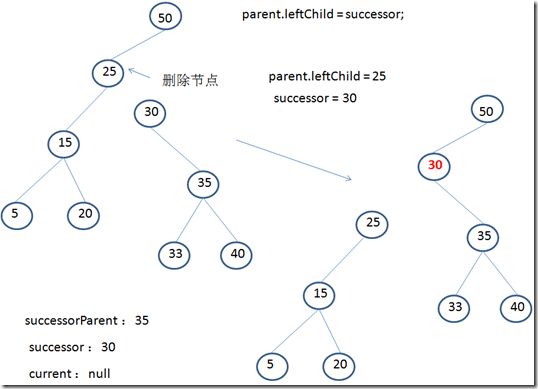
3.parent.leftChild = successor;
这一步主要作用是:后继替换删除节点
看到后继“30”跟主树连接起来。这里parent.leftChild(或parent.rightChild)是之前我们查找删除节点时,已经知道删除节点的具体位置,而parent引用就是删除节点的父节点。
此时,删除节点“25”的左子树端断开了与主树的连接,成为单独的一个子树。
4.successor.leftChild = current.leftChild;
这一步作用是:连接后继与删除节点的左子节点。
第3步中显示两棵树,这里实际上是真正删除节点“25”,因为“25”完全跟整棵树脱离的关系,一段时间后,会被java垃圾回收掉。
此时,删除包含两个字节点的操作全部完成。
删除完整代码:
/** * 删除节点 * * @param key 删除节点key值 * @return 返回值 */ public boolean delete(int key) { Node current = root; // 当前节点 Node parent = root; // 父节点,用于标记删除节点的父节点 boolean isLeftChild = true; // 是否是左子节点 // 查找要删除的节点 while (current.iData != key) { // 保存父节点的引用 parent = current; // 删除节点在左子树 if (key < current.iData) { isLeftChild = true; current = current.leftChild; } // 删除节点在左子树 else { isLeftChild = false; current = current.rightChild; } // 找不到删除节点,返回 if (current == null) { return false; } } // 删除没有子节点的节点 // 即删除节点为current,此时其左子节点、右子节点的应用都为null if (current.leftChild == null && current.rightChild == null) { if (current == root) { root = null; } else if (isLeftChild) { // 修改current父节点左子节点的引用 parent.leftChild = null; } else { // 修改current父节点右子节点的引用 parent.rightChild = null; } } // 删除节点current的右子节点为空,即只有左子节点 else if (current.rightChild == null) { // 判断是否为根 if (current == root) { root = current.leftChild; } // 如果删除节点为parent的左子节点,则引用赋值为左子树 else if (isLeftChild) { parent.leftChild = current.leftChild; } // 如果删除节点为parent的右子节点,则引用赋值为右子树 else { parent.rightChild = current.leftChild; } } // 删除节点current的左子节点为空,即只有右子节点 else if (current.leftChild == null) { // 判断是否为根 if (current == root) { root = current.rightChild; } // 如果删除节点为parent的左子节点,则引用赋值为左子树 else if (isLeftChild) { parent.leftChild = current.rightChild; } // 如果删除节点为parent的右子节点,则引用赋值为右子树 else { parent.rightChild = current.rightChild; } } else { // 找到后继 Node successor = getSuccessor(current); // 判断删除节点是否为根的情形 if (current == root) { root = successor; } else if (isLeftChild) { // 连接删除节点的父节点与后继节点 parent.leftChild = successor; } else { // 连接删除节点的父节点与后继节点 parent.rightChild = successor; } // 连接后继左子节点 successor.leftChild = current.leftChild; } return true; }
总结:
删除节点操作在二叉搜索树中是相对来说挺复杂的,但是只要理解其中的原理,删除操作还是很好写的。