排序算法

一、插入排序

1、直接插入排序

//直接插入排序

template<class T>

void insertSort(T array[],int n)

{

    T temp;

    for(int i = 1; i < n ; i++)//循环，i表示插入的趟数，共进行n-1趟插入

    {

        temp = array[i];//将待插入元素赋给temp

        int j = i-1;

        while(j >= 0 && temp < array[j])//把比temp大的元素向后移

        {

            array[j+1] = array[j];

            j--;

        }

        array[j+1] = temp;//j+1为temp的位置，将temp插入到这个位置

    }

}

利用有序表的插入操作，即将第p+1个元素插入到前面的p个元素中，插入位置后的元素进行后移。

2、折半插入排序

//折半插入排序

template<class T>

void BianryInsertSort(T array[],int n){

    for(int i = 1; i < n; i++)//共进行n-1次插入

    {

       int left = 0, right = i-1, mid;
       T  temp = array[i];//保存待插入数据

       while(left <= right)

       {

           mid = (left + right)/2;//求出中心点

           if(temp < array[mid])//如果待插入数据比中心点元素小

           {

               right = mid - 1;//更新右区间的值

           }

           else

               left = mid + 1;//更新左区间的值

       }

for(int j = i-1;j >= left; j--)//执行移动操作

           array[j+1] = array[j];
       array[left] = temp;//将待插入数据插入到有序表中

    }

}

3、希尔排序

//希尔排序（不稳定）

template<class T>

void ShellSort(T array[], int n){

    int d = n/2;//增量初始化为数组大小的一半

    while(d>=1)//循环遍历所有可能

    {

        for(int k = 0; k<d; k++)//遍历所有的子序列

        {

            for(int i=k+d; i<n; i+=d)//对每一个子序列执行插入排序

            {

                T temp = array[i];

                int j = i-d;

                while(j>=k && array[j] > temp){

                    array[j+d] = array[j];

                    j-=d;

                }

                array[j+d] = temp;

            }

        }

        d = d/2;//增量为上次的一半

    }

}

二、交换排序

1、冒泡排序

template<class T>
void BubbleSort(T array[], int n)

{

    for(int i = 0; i < n; i++)//外层循环控制排序的每一趟

    {

        for(int j = 1; j < n-i; j++)//内层循环控制本趟中的冒泡操作

        {

            if(array[j] < array[j-1])//如果是逆序的，则交换这两个元素

            {

                T temp = array[j];

                array[j] = array[j-1];

                array[j-1] = temp;

            }

        }

    }

}

 2、改进的冒泡排序

template<class T>

void BubbleSort2(T array[],int n)

{

    int flag = 0;//标记每一趟的冒泡排序过程中是否发生了交换

    for(int i = 0; i < n; i++)//外层循环控制排序的每一趟

    {

        flag = 0;

        for(int j = 0; j < n-i; j++)//内层循环控制本趟中的冒泡排序

        {

            if(array[j] < array[j-1])

            {

                flag = 1;

                T temp = array[j];

                array[j] = array[j-1];

                array[j-1] = temp;

            }

        }

        if(flag == 0)//如果某一趟的冒泡过程中没有发生交换则结束操作

               return;

    }



}

 四、选择排序

1、简单选择排序

void SelectSort(int array[],int n)

{

    for(int i = 1; i < n; i++)

    {

        int k = i-1;

        for(int j = i; j < n; j++)

        {

            if( array[j] < array[k] )

            {

                k = j;

            }

            if( k!= i-1)

            swap(array[k],array[i-1]);

        }

    }

}

利用线性查找的方法从一个序列中找到最小的元素

2、堆排序（不稳定）

template<class T>
void SiftDown(T array[], int i, int n)

{   //用来保持以结点i为根的最大堆的性质，n是所有元素的个数

    int l = 2*i + 1, r = 2*i + 2, min = i;//找到i结点的两个孩子的下标

    if(l < n && array[min] < array[l])//和左子结点进行比较

       min = l;

    if(r < n && array[min] < array[r])//和右子结点进行比较

       min = r;

    if(min != i)//判断是否进行调整

    {

        swap(array[min],array[i]);

        SiftDown(array,min,n);//递归对子结点进行调整

    }

}
template<class T>

void BuildHeap(T array[], int n)//创建一个最大堆

{

    int p = n/2 - 1;//求出非叶子结点的最大下标

    for(int i = p;i >= 0; i--)

    {

        SiftDown(array,i,n);

    }

}
template<class T>

void HeapSort(T array[],int n)

{

    BuildHeap(array,n);//首先建立一个最大堆

    for(int i = n-1; i > 0; i--)

    {

        swap(array[0],array[i]);

        BuildHeap(array,i);

    }

}

利用最大堆找到序列中的最大值，将 堆顶元素和当前最后一个元素进行交换，n = n-1；

五、归并排序

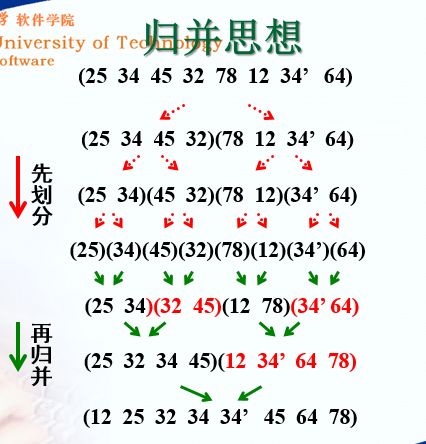
template<class T>

//归并函数

void Merge(T Data[],int start,int mid,int end)

{

    int len1 = mid - start + 1,len2 = end - mid;//分别表示两个归并区间的长度

    int i,j,k;

    T* left = new T[len1]; //临时数组用来存放Data[start,mid]数据

    T* right = new T[len2];//临时数组用来存放Data[mid+1,end];

    for(i = 0;i < len1; i++)//执行数据复制操作

       left[i] = Data[i+start];

    for(i = 0;i < len2; i++)//执行数据复制操作

       right[i] = Data[i+mid+1];

    i = 0,j = 0;

    for(k = start;k < end; k++)//执行归并

    {

        if( i == len1 || j == len2)

            break;

        if( left[i] <= right[j])

           Data[k] = left[i++];

        else

           Data[k] = right[j++];

    }

    while(i < len1)//若Data[start,mid]还有待归并数据，则放到Data后面

       Data[k++] = left[i++];

    while(j < len2)//对Data[mid+1,end]间的数据执行同样的操作

       Data[k++] = right[j++];

    delete[] left;//释放内存

    delete[] right;

}

template<class T>

void MergeSort(T Data[],int start,int end)

{//对Data[start]-Data[end]之间的序列进行归并排序

    if(start < end)

    {

        int mid = (start + end)/2;//计算中间位置

        MergeSort(Data,start,mid);//对左边子序列归并排序

        MergeSort(Data,mid+1,end);//对右边子序列归并排序

        Merge(Data,start,mid,end);//归并左、右两边的有序序列

    }

}

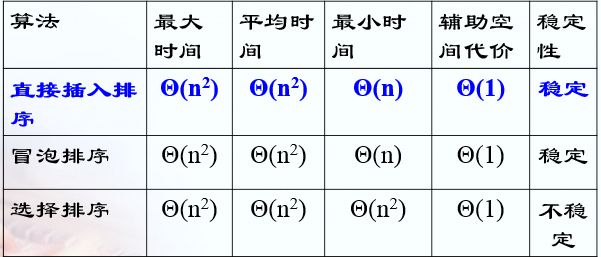
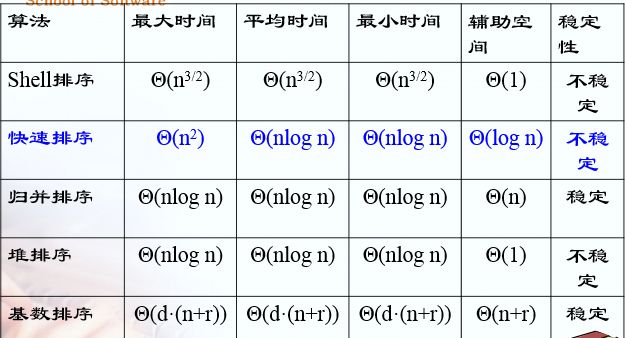
 各种排序算法的比较