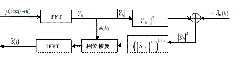基于Matlab的MMSE的语音增强算法的研究
本课题隶属于学校的创新性课题研究项目。2012年就已经做完了,今天一并拿来发表。
--基于谱减法的语音信号增强算法..................................................................... 1
一:语音增强技术概述........................................................................................ 3
三:语音信号的相关特性.................................................................................... 3
1. 1 语音信号具有短时平稳性.............................................................. 3
1.2.语音信号可以分为浊音和清音....................................................... 3
1.3.语音信号可以利用统计分析特征描述........................................... 4
3.1周期性噪声....................................................................................... 4
3.2脉冲噪声........................................................................................... 5
3.3宽带噪声........................................................................................... 5
3.4同声道语音干扰............................................................................... 5
3.5传输噪声........................................................................................... 5
四:国内外有关抗噪声技术的解决方案............................................................ 5
(1) 基于谱减法的语音增强................................................................... 6
(2) 自适应滤波法的语音增强............................................................... 6
(3) 短时对数谱的MMSE语音增强...................................................... 6
2 寻找稳健的语音特征作为特征参数......................................................... 6
3 基于模型参数自适应的噪声补偿算法..................................................... 6
五:语音增强算法的三种具体算法分析与比较................................................ 6
(1) 谱减法算法的理论分析................................................................... 6
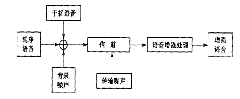
(2) 通过语音增强技术改善语音质量的过程....................................... 7
(3) 谱减法的流程图............................................................................... 7
(4)谱减法原理图.................................................................................... 8
2:自适应噪声抵消法.................................................................................. 9
(1) 自适应滤波器原理........................................................................... 9
(2) 结构框图......................................................................................... 10
3:短时对数谱的MMSE语音增强算法................................................... 11
六:实验环境(matlab)简介........................................................................... 13
七:算法的实现及仿真结果.............................................................................. 14
一:语音增强技术概述
在通信过程中语音受到来自周围环境、传输媒介引入的噪声,使接收到的语音信号并非纯净的原始语音信号,而是受噪声污染的带噪语音信号。这里的“噪音”定义为所需语音信号以外的所有干扰信号。
干扰信号可以是窄带的或宽带的、白噪声的或有色噪声的、声学的或电学的、加性的或乘性的,甚至可以是其它无关的语音。由噪声导致的语音质量的下降会使许多语音处理系统的性能急剧恶化。采用语音增强技术进行预处理,可有效地改善系统性能。
二:语音增强的目的
对收听人而言主要是改善语音质量,提高语音可懂度,减少疲劳感;对语音处理系统(识别器、声码器、手机)而言是提高系统的识别率和抗干扰能力。
三:语音信号的相关特性
语音增强与语音信号处理理论有关,而且涉及到人的听觉感知和语音学。噪声来源众多,随应用场合不同而特性各异,因此难以找到一种通用的语音增强算法可以适用于各种噪声环境,必须针对不同环境下的噪声采取不同的语音增强策略。因此,要进行语音增强首先要了解语音特性、人耳感知特性和噪声特性。
1 语音特性
1. 1 语音信号具有短时平稳性
声道形状有相对稳定性,在一段时间内(10ms~30ms),人的声带和声道形状是相对稳定的,可认为其特征是不变的,因而语音的短时谱具有相对稳定性,在语音分析中可以把语音信号分为若干分析帧,每一帧的语音可以认为是准稳定的。语音增强可以利用这种短时平稳性。
1.2.语音信号可以分为浊音和清音
语音可以分为周期性的浊音和非周期性的清音。在语音增强中,可以利用浊音的周期性特征,采用梳状滤波器提取语音分量或者抑制非语音信号,而清音则难以与宽带噪声区分。
1.3.语音信号可以利用统计分析特征描述
作为一个随机过程,语音信号可以利用许多统计分析特征进行分析。语音的短时谱幅度统计特征是时变的,只有当分析帧长趋于无穷大时,才能近似具有高斯分布。在高斯模型的假设中,可以认为傅里叶展开系数是独立的高斯随机变量,均值为零,而方差是时变的。在有限帧长时这种高斯模型只是一种近似的描述,可以作为分析的前提在宽带噪声污染的带噪语音增强中应用。
2 人耳感知特性
人耳对语音的感知主要是通过语音信号频谱分量幅度获取的,对各分量相位则不敏感,对频率高低的感受近似与该频率的对数值成正比。人耳具有掩蔽效应,人耳除了可以感受声音的强度、音调、音色和空间方位外,还可以在两人以上的讲话环境中分辨出所需要的声音,这种分辨能力是人体内部语音理解机制具有的一种感知能力。人类的这种分离语音的能力与人的双耳输入效应有关,称为“鸡尾酒会效应”。语音增强的最终效果度量是人耳的主观感觉,所以在语音增强中可以利用人耳感知特性来减少运算代价。
3 噪声特性
根据与输入语音信号的关系,噪声可分为加性噪声和非加性噪声两类。对某些非加性噪声而言,可以通过一定的变换转换成加性噪声。语音处理中的加性噪声大体上可以分为周期性噪声、脉冲噪声、宽带噪声和同声道其他语音的干扰等。
3.1周期性噪声
周期性噪声主要来源于发动机等周期性运转的机械,电气干扰也会引起周期性噪声。特点是频谱上有许多离散的线谱。实际信号受多种因素的影响,线谱分量通常转变为窄带谱结构,而且通常这些窄带谱都是时变的,位置也不固定。必须采用自适应滤波的方法才能有效地区分这些噪声分量。
3.2脉冲噪声
脉冲噪声来源于爆炸、撞击、放电及突发性干扰等。特征是时间上的宽度很窄。在时域消除脉冲噪声过程如下:根据带噪语音信号幅度的平均值确定阈值。当信号超出这一阈值时判别为脉冲噪声。然后对信号进行适当的衰减,就可完全消除噪声分量,也可以使用内插方法将脉冲噪声在时域上进行平滑。
3.3宽带噪声
宽带噪声来源很多,热噪声、气流噪声及各种随机噪声源、量化噪声都可以视为宽带噪声。宽带噪声与语音信号在时域和频域上基本上重叠,只有在无话期间,噪声分量才单独存在。因此消除这种噪声比较困难。对于平稳的宽带噪声,通常可以认为是白色高斯噪声。
3.4同声道语音干扰
干扰语音信号和待传语音信号同时在一个信道中传输所造成的语音干扰称为同声道语音干扰。区别有用语音和干扰语音的基本方法是利用它们的基音差别。考虑到一般情况下两种语音的基音不同,也不成整数倍,这样可以用梳状滤波器提取基音和各次谐波,再恢复出有用语音信号
3.5传输噪声
这是传输系统的电路噪声。处理这种噪声可以采用同态处理的方法,把非加性噪声变换为加性噪声来处理。
四:国内外有关抗噪声技术的解决方案
目前国内外有关抗噪声技术的的研究成果的三类解决方法:
1 语音增强算法
采用语音增强算法,提高语音识别系统前端预处理的抗噪声能力,提高输入信号的信噪比。
(1) 基于谱减法的语音增强
(2) 自适应滤波法的语音增强
(3) 短时对数谱的MMSE语音增强
2 寻找稳健的语音特征作为特征参数
寻找稳健的语音特征作为特征参数,实验证明,这类参数对宽带语音具有较好的抗噪性;
3 基于模型参数自适应的噪声补偿算法
五:语音增强算法的三种具体算法分析与比较
1:谱减法
(1) 谱减法算法的理论分析
谱减法是利用噪声的统计平稳性以及加性噪声与语音不相关的特点而提出的一种语音增强方法。这种方法没有使用参考噪声源,但它假设噪声是统计平稳的,即有语音期间噪声的幅度谱的期望值与语音间隙噪声的幅度谱的期望值相等。用无语音间隙测量计算得到的噪声频谱的估计值取代有语音噪声的频谱,与含噪声语音频谱相减,得到语音频谱的估计值。当上述差值得到的负的幅度值时,将其置零。由于人耳对语音的感知主要是通过语音信号中各频谱分量幅度获得的,对各分量的相位不敏感。因此,此类语音增强方法将估计的对象放在短时谱幅度上。
假设带噪信号为:
y(n)=s(n)+d(n),0<=n<=N-1
其中s(n)为纯净语音,d(n)为平稳加性噪声,y(n)通常需要加窗处理来消除分帧是带来的阶段效应,这里为方面依然使用y(n)表示加窗处理后的带噪信号。由于实际的分析帧长有限,傅里叶系数之间存在着一定的相关性。假设s(n)满足高斯分布,其傅里叶变换相当于多个高斯样本的加权和,仍然可以认为满足高斯分布,均值为0,方差可以通过无语音期间的噪声分析得到。基于短时谱幅度估计的语音增强就是利用已知的噪声功率谱信息,从中估计出。由于人耳对相位不敏感,为此只要估计出Sk,然后利用带噪语音的相位,进行傅里叶反变换就可得到增强的语音。基于语音短时谱估计方法的一般原理如下所示。根据实现估计的方法不同,可以分为谱减法,维纳滤波法和最小均方误差
谱减法在频域将带噪语音的功率谱减去噪声的功率谱得到纯净语音功率谱估计,开方后就得到语音幅度谱估计,用带噪语音的相位来近似纯净语音的相位,再采用反傅里叶变换回复时域信号。它的有点是比较简单,只需要进行反傅里叶变换,而且实时实现较容易。但谱减法适用的信噪比范围较窄,在信噪比较低时对语音的可懂度损伤最大,这是因为信噪比主要代表了由浊音决定的大信号能量,而语音可懂度主要取决于元音和相对较小的代表辅音的信号。所以,实际应用时除了要降低噪声外,还要兼顾语音的可懂度和自然度。另外,由于频谱直接相减会使增强后的语言产生“音乐噪声”,它具有一定的节奏性,听上去类似音乐声,由此而得名。
(2) 通过语音增强技术改善语音质量的过程
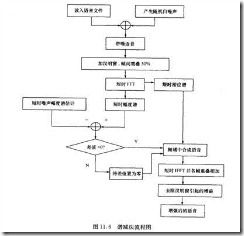
(3) 谱减法的流程图
利用噪声的统计平稳性以及加性噪声与语音不相关的特点而提出的一种语音增强方法。没有使用参考噪声源,但它假设噪声是统计平稳的,即有语音期间噪声幅度谱的期望值与无语音间隙噪声的幅度谱的期望值相等。用无语音间隙测量计算得到的噪声频谱的估计值取代有语音期间噪声的频谱,与含噪语音频谱相减,得到语音频谱的估计值。此类语音增强方法将估计的对象放在短时谱幅度上。
(4)谱减法原理图
谱相减的物理意义:相当于对带噪语音的每一个频谱分量乘以一个系数。信噪比高时,含有语音的可能性大,衰减系数小。反之,则认为含有语音的可能性小,衰减系数大。
谱减法在频域将带噪语音的功率谱减去噪声的功率谱得到纯净语音功率谱估计,开方后就得到语音幅度谱估计,用带噪语音的相位来近似纯净语音的相位,再采用反傅里叶变换恢复时域信号。
谱减法优点:比较简单,只需要进行正反傅立叶变换,而且实时实现较容易。
谱减法缺点:适用的信噪比范围较窄,在信噪比较低时对语音的可懂度损伤较大。所以实际应用时除了要降低噪声外,还要兼顾语音的可懂度和自然度。
由于频谱直接相减会使增强后的语音产生“音乐噪声”,它具有一定的节奏性,听上去类似音乐声,由此而得名。
2:自适应噪声抵消法
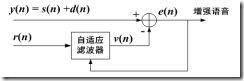
设带噪语音输入为y(n)=s(n)+d(n), s(n)为语音信号,d(n)为未知噪声信号,r(n)参考噪声输入,也即自适应滤波器的输入,v(n)是该滤波器的输出。 r(n)与s(n)无关,而与d(n)相关。
(1) 自适应滤波器原理
在输入过程的统计特性未知或是输入过程的统计特性变化时,能够调整自己的参数,以满足某种最佳准则的要求。自适应滤波的目的就是通过对 r(n)的滤波,使输出的噪声估值v(n)尽可能接近带噪语音中的d(n),然后从带噪语音中直接减去 v(n) ,达到语音增强的目的。
自适应滤波器通常采用FIR滤波器,系数采用最小均方误差(MMSE)准则来迭代估计。判断标准是使误差信号e(n)能量最小:
其中,wk是滤波器系数,N是滤波器抽头数。MMSE准则要求噪声和语音相互独立,这时,误差信号e(n)能量最小,可保证v(n)与d(n)最接近。
自适应滤波器
自适应滤波器是能够根据输入信号自动调整性能进行数字信号处理的数字滤波器。作为对比,非自适应滤波器有静态的滤波器系数,这些静态系数一起组成传递函数。
对于一些应用来说,由于事先并不知道所需要进行操作的参数,例如一些噪声信号的特性,所以要求使用自适应的系数进行处理。在这种情况下,通常使用自适应滤波器,自适应滤波器使用反馈来调整滤波器系数以及频率响应。
总的来说,自适应的过程涉及到将价值函数用于确定如何更改滤波器系数从而减小下一次迭代过程成本的算法。价值函数是滤波器最佳性能的判断准则,比如减小输入信号中的噪声成分的能力。
随着数字信号处理器性能的增强,自适应滤波器的应用越来越常见,时至今日它们已经广泛地用于手机以及其它通信设备、数码录像机和数码照相机以及医疗监测设备中。
(2) 结构框图
下面图示的框图是最小均方滤波器(LMS)和递归最小平方(en:Recursive least squares filter,RLS)这些特殊自适应滤波器实现的基础。框图的理论基础是可变滤波器能够得到所要信号的估计。
在开始讨论结构框图之前,我们做以下假设:
可变滤波器有有限脉冲响应结构,这样结构的脉冲响应等于滤波器系数。![]() 阶滤波器的系数定义为
阶滤波器的系数定义为
误差信号或者叫作代价函数,是所要信号与估计信号之差
可变滤波器通过将输入信号与脉冲响应作卷积估计所要信号,用向量表示为
其中
是输入信号向量。另外,可变滤波器每次都会马上改变滤波器系数
其中 ![]() 是滤波器系数的校正因子。自适应算法根据输入信号与误差信号生成这个校正因子,LMS 和 RLS 是两种不同的系数更新算法。
是滤波器系数的校正因子。自适应算法根据输入信号与误差信号生成这个校正因子,LMS 和 RLS 是两种不同的系数更新算法。
3:短时对数谱的MMSE语音增强算法
分别表示带噪语音 y(t) 、信号 x(t) 和噪声d(t) 进行FFT变换后的第k个频谱分量。语音增强的任务就是利用已知的噪声功率谱信息,从 y(t) 中估计出x(t) ,即由{Y0 , Y1 , L }估计出Xk 。这里仅对频谱幅度的对数感兴趣,而认为相位对语音质量影响不大,带噪语音的短时谱可用快速傅里叶变换一帧的计算得到,其相位提取后存储起来,然后对纯净语音的短时对数谱作最小均方误差估计。处理后的语音由估计得到的幅度谱和相位重建。因而估值可以简化为估计Ak 。Ak的估计式可写成 ![]()
六:实验环境(matlab)简介
MATLAB是矩阵实验室(Matrix Laboratory)的简称,和Mathematica、Maple并称为三大数学软件。它在数学类科技应用软件中在数值计算方面首屈一指。MATLAB可以进行矩阵运算、绘制函数和数据、实现算法、创建用户界面、连接其他编程语言的程序等,主要应用于工程计算、控制设计、信号处理与通讯、图像处理、信号检测、金融建模设计与分析等领域。
MATLAB的基本数据单位是矩阵,它的指令表达式与数学、工程中常用的形式十分相似,故用MATLAB来解算问题要比用C,FORTRAN等语言完相同的事情简捷得多,并且mathwork也吸收了像Maple等软件的优点,使MATLAB成为一个强大的数学软件。在新的版本中也加入了对C,FORTRAN,C++ ,JAVA的支持。可以直接调用,用户也可以将自己编写的实用程序导入到MATLAB函数库中方便自己以后调用,此外许多的MATLAB爱好者都编写了一些经典的程序,用户可以直接进行下载就可以用。
要求利用MATLAB来读入(采集)语音信号,将它赋值给某一向量。再将该向量看作一个普通的信号,对其进行FFT变换实现频谱分析,再依据实际情况对它进行滤波。然后我们还可以通过sound命令来对语音信号进行回放,以便在听觉上来感受声音的变化。
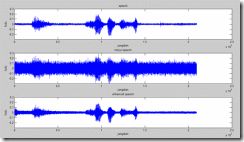
七:算法的实现及仿真结果
该算法是利用Matlab进行仿真的。通过对时域波形的观察,表明MMSE的语音增强算法能够有效地滤除背景噪声,在用了有声/无声判断后,“音乐噪声”也大幅度降低。
八:附件
Matlab代码
clear all
%-----------------读入语音文件------------------------
[speech,fs,nbits]=wavread('chunge.wav');
%------------------读入数据-----------------------------
%------------------参数定义-----------------------------
winsize=256; %窗长
n=0.04; %噪声水平
size=length(speech); %语音长度
numofwin=floor(size/winsize); %帧数
ham=hamming(winsize)'; %产生汉明窗
hanwin=zeros(1,size); %定义汉明窗的长度
enhanced=zeros(1,size); %定于增强语音的长度
clean=zeros(1,winsize);
x=speech'+n*randn(1,size); %产生带躁信号
noisy=n* randn(1,winsize);
N=fft(noisy); %对噪声傅里叶变换
nmag=abs(N); %噪声功率谱
%-------------------分帧-------------------------
for q=1:2*numofwin-1
frame=x(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2);
%-------------------对带躁语音帧间重叠一半取值--------------------
hamwin(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2)=...
hamwin(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2)+ham;
%-------------------加窗----------------------------------
y=fft(frame.*ham); %对带躁语音傅里叶变换
mag=abs(y); %噪声语音功率谱
phase=angle(y); %带躁语音相位
%-------------------幅度谱减---------------------------------------------------
for i=1:winsize
if mag(i)-nmag*(i)>0
clean(i)=mag(i)-nmag(i);
else
clean(i)=0;
end
end
%-----------------在频域中重新合成语音---------------------------------------------
spectral=clean.*exp(1i*phase);
%-----------------反傅里叶变换并重叠相加----------------------------------------
enhanced(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2) =...
enhanced(1+(q-1)*winsize/2:winsize+(q-1)*winsize/2)+real(ifft(spectral))
end
%------------------除去汉明窗引起的增益--------------------------------------
for i=1:size
if hanwin(i)==0
enhanced(i)=0
else
enhanced(i)=enhanced(i)/hanwin(i);
end
end
%计算增强前后的信噪比
%SNR1=10*log10(var(speech')/var(noisy));
%加躁语音信噪比
%SNR2=10*log10(var(speech')/var(enhanced-speech'));
%增强语音信噪比
wavwrite(x,fs,nbits,'noisy.wav');
%输出带躁信号
wavwrite(enhanced,fs,nbits,'enhanced.wav')
%输出增强信号
%---------------画波形
figure(1);
subplot(3,1,1);
plot(speech');
title('yuanshiyuyinboxing');
xlabel('yangdianshu');
ylabel('fudu');
axis([0 2.5*10^4-0.3 0.3]);
subplot(3,1,2);
plot(x);
title('jiazaoyuyinboxing')
xlabel('yangdianshu');
ylabel('fudu');
axis([0 2.5*10^4-0.3 0.3]);
subplot(3,1,3);
plot(enhanced);
title('zengqiangyuyinboxing');
xlabel('yangdianshu');
ylabel('fudu');
axis([0 2.5*10^4-0.3 0.3]);
九:参考文献
张雪英著《数字语音处理及matlab仿真》 电子工业出版社 2010
Steven W Smith 《实用数字信号处理-从原理到应用》人民邮电出版社 2007
A V奥本海姆 《离散时间信号处理》西安交通大学出版社 1999