大话数据结构-查找

查找

这里介绍查找分为二分法查找、插值查找、斐波那契查找、二叉排序树查找，都是查找一个数组里面的一个元素。

二分法查找

把数组不断对半折叠，直到找到元素。

public class search {
    private int[] a;
    private int key;
    public search(int[] a, int key){
        this.a = a;
        this.key = key;
    }
    //二分法寻找
    //把数组的首尾索引取中间，与搜索的元素比较后再更改首尾索引
    public void binary_search(){
        int search_count = 0;
        int low_index = 0;//首
        int high_index = a.length-1;//尾
        int middle_index = (low_index+high_index)/2;//二分法取中间进行比较
        while(a[middle_index]!=key){//直到相等为止
            search_count = search_count+1;
            if(key>a[low_index] && key<a[middle_index]){//查找值接近首
                high_index = middle_index;//尾巴变为中间值
            }
            if(key>a[middle_index] && key<a[high_index]){//查找值接近尾
                low_index = middle_index;//首变成中间值
            }
            //(low_index+high_index)/2 = low_index+(high_index-low_index)/2
            middle_index = low_index+(high_index-low_index)/2;
        }
        System.out.println("binary_search的查找次数："+search_count+";返回索引："+middle_index);
    }
 }

插值查找

二分查找只考虑到了查找值接近首还是接近尾，但是没有考虑到多接近的问题。
插值查找不再用首尾的一半作为增量（二分法中其实就是low = low + （high-low）/2；（high-low）/2是增量）而是使用以下为增量

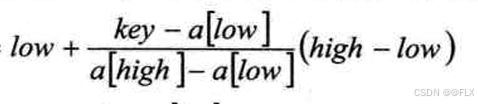
key是查找值，(key-a[low])/(a[high]-a[low])是小于1的值，是把按照key到a[low]的距离占数组总长的占比，占比越大，说明key越接近high，此时增量也就越大。

public class search {
    private int[] a;
    private int key;
    public search(int[] a, int key){
        this.a = a;
        this.key = key;
    }
    //插值寻找
    public void interpolation_search(){
        int search_count = 0;
        int low_index = 0;
        int high_index = a.length-1;
        int middle_index2 = low_index + (int)((high_index-low_index)*((key-a[low_index])*1.0/(a[high_index]-a[low_index])));
        while(a[middle_index2]!=key){
            search_count = search_count+1;
            if(key>a[low_index] && key<a[middle_index2]){
                high_index = middle_index2;
            }
            if(key>a[middle_index2] && key<a[high_index]){
                low_index = middle_index2;
            }
            middle_index2 = low_index + (int)((high_index-low_index)*((key-a[low_index])*1.0/(a[high_index]-a[low_index])));
        }
        System.out.println("interpolation_search的查找次数："+search_count+";返回索引："+middle_index2);
    }
}

斐波那契查找

斐波那契查找进一步改善增量，把增量改为整个数组长度的0.618，斐波那契数列的每一个元素和前一个元素的比很接近0.618，比如，斐波那契数列{1，1，2，3，5，8}：3：2≈5：3≈8：5；如果整个数组的长度为8，规定每次增量为0.618*high，那mid = low+5；增量为5；如果key>a[mid]，也就是key在八分之三里面，那么数组长度变为3，接下来增量为mid = low+2；如果key

public class search {
    private int[] a;
    private int key;
    public search(int[] a, int key){
        this.a = a;
        this.key = key;
    }
    //斐波那契查找
    public void fabonacci_search(){
        int n = a.length-1;
        //生成有n个元素的斐波那契数列
        double[] feibonacci_array = new double[n+1];
        feibonacci_array[0] = 0;feibonacci_array[1] = 1;
        int count = 0;
        while((count+2)<=n){
            feibonacci_array[count+2] = feibonacci_array[count]+feibonacci_array[count+1];
            count = count+1;
        }
        //在fabonacci_array中找到大于但最接近n的元素
        count = 0;
        while(n>feibonacci_array[count]){
            count = count+1;
        }
        //扩充a数组的长度为feibonacci_array[count]，方便对数组进行黄金分割
        for (int i = n; i < count; i++) {
            a[i] = a[n];//把数组最后几个设置为相等
        }
        //按照黄金分割来确定mid
        int low = 0;
        int high = n;
        int mid = low+(int)feibonacci_array[count-1];
        int count2 = 0;
        while(a[mid]!=key){
            count2 = count2+1;
            if(key>a[mid]){//key在八分之三里面，数组长度变为3，count = count-2
                low = mid;
                count = count -2;
            }
            else if(key<a[mid]) {//key在八分之五里面，数组长度变为5，count = count-1
                high = mid;
                count = count-1;
            }
            mid = low+(int)feibonacci_array[count-1];
        }
        if(mid>n){
            System.out.println("fabonacci_search的查找次数："+count2+";返回索引：NULL");
        }
        else {
            System.out.println("fabonacci_search的查找次数："+count2+";返回索引："+mid);
        }
    }
}

二叉排序树查找

二叉排序树的本意是用来解决查找到key后对key进行删除或者插入操作不便的问题。二叉排序树查找后进行删除或者插入无需改动大部分的数据。


注意：
1、有一个二叉排序树，插入一个节点，无需改变其他节点的位置。
2、二叉排序树进行中序遍历后为从小到大的
3、二叉排序树的节点结构：

//二叉树结点结构
class TreeNode {
  int val;
  TreeNode left;
  TreeNode right;
  TreeNode() {}
  TreeNode(int val) { this.val = val; }
  TreeNode(int val, TreeNode left, TreeNode right) {
      this.val = val;
      this.left = left;
      this.right = right;
  }
}

4、二叉树的查找
采用递归，终止条件时节点的val等于key，当key<当前节点的val时从左子树递归，>的时候从右子树递归

class TreeProcess{
    public TreeNode f = new TreeNode();//用来记录查找到的节点的双亲节点
    public TreeNode p = new TreeNode();//用来记录查找到的节点位置
    //查找
    public boolean Search_treenode(TreeNode T,int search_node){
        if(T==null){
            return false;
        }

        if(search_node == T.val){
            p = T;//找到的时候进行节点的记录
            return true;
        } else if (search_node < T.val) {//查找值小于当前节点时从左节点继续比较
            f = T;//记录双亲节点，查找不到则f为最后遍历节点
            return Search_treenode(T.left,search_node);
        }
        else {//查找值大于当前节点时从右节点继续比较
            f = T;//记录双亲节点，查找不到则f为最后遍历节点
            return Search_treenode(T.right,search_node);
        }

    }
}

5、二叉排序树的插入
插入之前先做一次查找，查找不到就进行插入，如果将一个数组的第一个元素作为跟节点，将数组的其他元素进行依次插入，再对二叉树进行中序遍历，那么可以得到从小到大的排序数组。

class TreeProcess{
    public TreeNode f = new TreeNode();//用来记录查找到的节点的双亲节点
    public TreeNode p = new TreeNode();//用来记录查找到的节点位置
    //查找不到的时候进行插入
    public boolean Insert_Treenode(TreeNode T,int insert_node){
        TreeNode s = new TreeNode(insert_node);
        if(!Search_treenode(T, insert_node)){//查找后找不到f为最后遍历节点
            if(insert_node<f.val){//小于f接在左子树
                f.left = s;
            } else if (insert_node>f.val) {//大于f接在右子树
                f.right = s;
            }
            return true;
        }else {
            return false;
        }
    }
}

6、数组转二叉排序树
有了查找和插入，就可以进行数组转二叉排序树

//数组转化为二叉排序树
    public TreeNode ArrayToTree(int[] array){

        TreeNode T = new TreeNode(array[0]);
        for (int i = 1; i < array.length; i++) {
            Insert_Treenode(T,array[i]);
        }
        return T;

    }
    //中序遍历二叉排序树
    //遍历结果存储于动态数组list
    public void zhongxubianli(List<Integer> list,TreeNode T){
        if(T == null){
            return ;
        }
        zhongxubianli(list , T.left);
        list.add(T.val);
        zhongxubianli(list , T.right);
    }

7、二叉排序树删除节点
节点有四种情况：
（1）没有左节点，只有右节点：删除节点，把右子树接到节点上，一般删除节点可以把右节点的val复制给节点，然后把右节点的左右节点信息复制给节点，然后释放右节点的所有信息。这样节点的父节点不用改变他的左右节点信息。

（2）没有右节点，只有左节点：删除节点，把左子树接到节点上。

（3）没有左右节点：删除节点，如果节点是父节点的右节点，父节点的右节点设置为null，如果节点是父节点的左节点，父节点的左节点设置为null。

（4）左右节点都有：

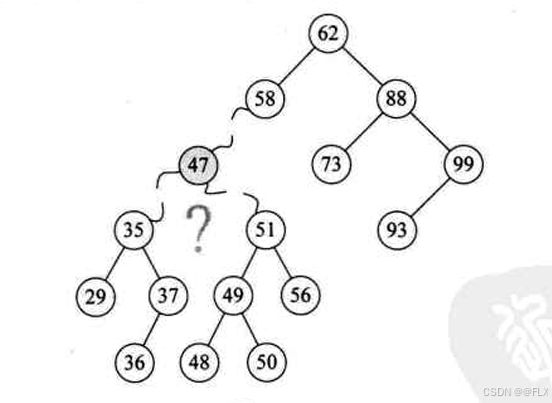
如图删除47，如果对二叉排序树进行中序遍历，那么47附近的节点是：35、36、37、47、48；47的左右两边是37和48，可以把47的左子树中的最大值37接替47的位置，或者47的右子树的最小值48代替47的位置。这里使用左子树的最大值代替。
左子树的最大值可以进行查找：47的左节点一直往右，直到最后一个右节点就是37。
可以把37的值复制给47节点，然后对37节点的左右节点进行处理：
如果37只有左节点或者只有右节点：把左节点/右节点接到37上；
如果37没有左右节点，删除37节点。

class TreeProcess{
    public TreeNode f = new TreeNode();//用来记录查找到的节点的双亲节点
    public TreeNode p = new TreeNode();//用来记录查找到的节点位置
    //delete
    public boolean Treenode_Delete(TreeNode T,int delete_node){
        //TreeNode p = new TreeNode();
        TreeNode s = new TreeNode();
        if(!Search_treenode(T,delete_node)){
            return false;
        }else {
            if(p.right==null && p.left != null){//没有右子树，左子树直接接上去
                p.val = p.left.val;
                p.right = p.left.right;//注意这里这条语句跟吓一跳语句不能写反，不能先改变p.left
                p.left =p.left.left;
            }else if(p.left == null && p.right!=null){//没有左子树，右子树直接接上去
                p.val = p.right.val;
                p.left = p.right.left;
                p.right = p.right.right;

            }else if (p.right==null && p.left == null) {//没有左子树没有右子树，直接删掉
                if(f.left == p){f.left = null;}
                if(f.right == p){f.right = null;}
            }else if(p.right!=null && p.left != null){//两边都有
                s = p.left;
                while (true){
                    if(s.right!=null){
                        if(s.right.right==null){//这样写是为了获取最右节点的父节点，对父节点的左/右节点设置为null
                            p.val = s.right.val;
                            if(s.right.left!=null){//如果最右节点有左节点，那么左节点接到最右节点的位置
                                s.right = s.right.left;
                            }else {//最右节点没有左节点
                                s.right = null;
                            }
                            break;
                        }
                    } else {
                        p.val = s.val;
                        p.left = s.left;
                        break;
                    }
                    s = s.right;
                }
            }
        }
        return true;
    }
}