搜广推校招面经八十一

OPPO搜广推一面面经

一、介绍一下PLE模型

在多任务学习（Multi-Task Learning, MTL）中，多个任务共享部分模型结构，以提升整体效果。然而，不同任务间存在 任务冲突（Task Conflict） 问题，即不同任务对参数的优化方向不一致，导致性能下降。

论文：Tang, Hongyan, et al. “Progressive Layered Extraction (PLE): A Novel Multi-Task Learning (MTL) Model for Personalized Recommendations.” RecSys 2020.

PLE 的核心思想是：

通过引入多个专家网络（Experts）并区分共享专家与特定任务专家，结合门控机制（Gating Network）实现任务间知识共享与隔离的平衡。

1.1. 核心架构

• 专家网络（Experts）：
  • Shared Experts：供所有任务共享
  • Task-Specific Experts：只供特定任务使用
• 门控网络（Gating Network）：
  • 每个任务都有自己的门控网络，决定该任务在当前层中应从哪些专家中获取信息
  • 输出为每个专家的加权系数
• 塔结构（Tower）：
  • 每个任务最终仍保留独立的塔（MLP），用于完成最终预测

1.2. CGC（Customized Gate Control）结构

• 为了解决任务之间的“跷跷板”效应或负迁移效应，MMoE引入了任务独有的gate（expert是共享的，但gate是任务独有的，即不同任务通过gate共享相同的expert）
• CGC在共享expert之外，新增了task specific expert，即每个任务单独的expert，这些expert是专门用于对应任务的优化的。CGC既能享受到共享特征带来的好处，也有专有的expert为不同任务提供独自的优化空间。每一个任务的Tower网络都获取相应任务独享的专家网络输出和共享的专家网络输出
  

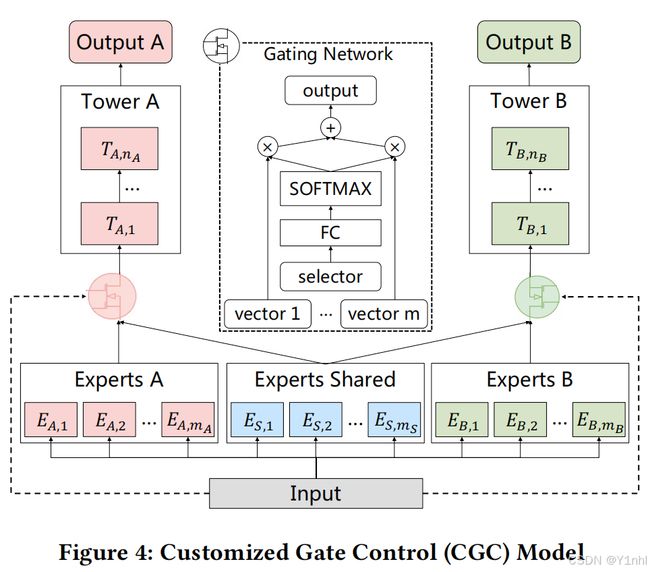
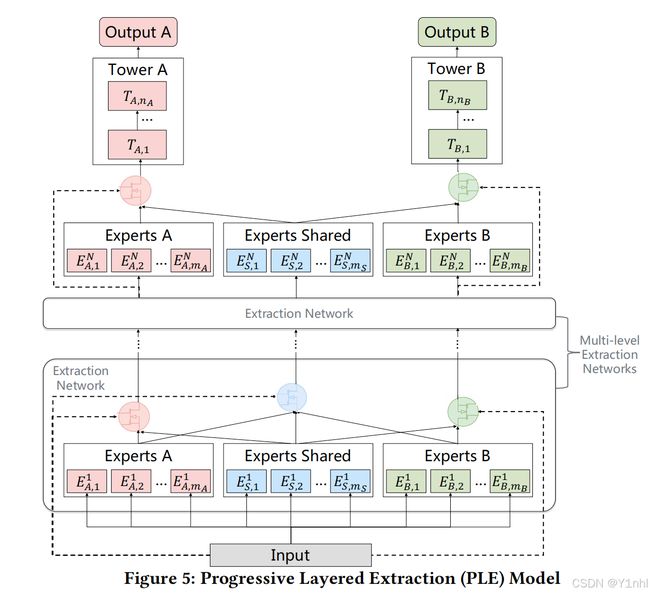
1.3. PLE就是Extraction Network + 多层CGC的架构

CGC中门控网络的个数等于任务的个数，而Extraction Network中除了对应任务的门控网络外，还有一个共享的门控网络。高层Extraction Network的输入不是原始的输入，而是包含更抽象语义的底层Extraction Network的门控融合输出。
Extraction Network结构 + CGC结构 如下图：

二、模型一般用什么优化器来训练，Adam优化器的原理，用过哪些优化器，有过对参数的调整吗？

感觉用得最多的必然是Adam了，原理介绍见【搜广推校招面经十三】

三、深度学习怎么防止过拟合，L1和L2正则化的区别

见【搜广推校招面经二十，搜广推校招面经十四，搜广推校招面经三十一】

四、排序模型和分类模型输入是一样的吗，输出有什么差别

4.1. 输入：基本一致

排序模型（Ranking Model）和分类模型（Classification Model）在输入特征方面是类似的，通常都是一组结构化的特征向量，反正都是二维的表格。这些特征可以包括数值型、类别型、文本向量化表示等，经过处理（如归一化、Embedding）后送入模型。

4.2. 输出：存在本质差异

项目	分类模型（Classification）	排序模型（Ranking）
输出形式	各类别的概率或标签	候选项的排序分数或排名
任务目标	预测所属类别	判断多个样本之间的相对排序
应用示例	图片识别：猫 / 狗 / 鸟	推荐系统：为用户排序商品
损失函数常用	CrossEntropyLoss、FocalLoss	Pairwise：Hinge loss、BPR Listwise：Softmax Cross Entropy、LambdaRank
预测方式	选最大概率的类别	根据得分排序候选项

4.3. pointwise、pairwise、listwise建模排序模型

见【搜广推校招面经二十九】
排序任务可以根据建模的方式分为三类：Pointwise、Pairwise 和 Listwise，主要区别在于它们如何构造训练样本以及如何定义损失函数。

4.3.1. Pointwise 方法

• 思想：将排序任务看作回归或分类问题，分别对每个样本预测一个相关性得分或标签。
• 建模方式：
  • 每个样本是一个独立的 query-document 对
  • 预测其与 query 的相关性得分或是否点击（0/1）
• 常用模型/损失函数：
  • 回归：MSE（Mean Squared Error）
  • 分类：CrossEntropyLoss、LogLoss
• 缺点：
  • 忽略了样本之间的相对关系，排序效果可能不佳

4.3.2. Pairwise 方法

• 思想：将排序任务转化为二分类问题，学习成对样本的相对顺序（谁排在前面）。
• 建模方式：
  • 输入为两个文档对 (di, dj)，同属于一个 query
  • 模型学习 di 是否比 dj 更相关
• 常用模型/损失函数：
  • RankNet：使用 $sigmoid(scor{e}_i-scor{e}_j)$
  • BPR（Bayesian Personalized Ranking）
  • Hinge loss（如 SVMRank）
• 缺点：
  • 样本数量为 O(n²)，训练成本高

4.3.3. Listwise 方法

• 思想：直接以整个候选列表为输入，优化整个排序列表的质量。
• 建模方式：
  • 训练样本为一个 query 对应的多个文档列表
  • 模型学习整个列表的最优排列顺序
• 常用模型/损失函数：
  • ListNet、ListMLE（优化列表似然）
  • LambdaRank、LambdaMART（基于 NDCG 等指标的优化）
• 优点：更适合优化排序指标（如 NDCG、MAP）

4.3.4. 三种方法对比表

方法	输入粒度	损失目标	优点	缺点
Pointwise	单个样本	回归/分类损失	实现简单，易于训练	无法建模样本间排序关系
Pairwise	样本对	相对顺序损失	引入相对信息，排序效果好	样本量大，训练时间较长
Listwise	整个样本列表	列表级排序指标	排序效果最佳	实现复杂，训练成本高

五、NDCG（Normalized Discounted Cumulative Gain）计算方法

NDCG 是一种常用的排序评估指标，衡量推荐结果的相关性和排序位置。值越高，说明模型越好。其核心思想是：

• 相关性越高的项排在越前面越好
• 靠前位置的重要性更高（打折）

Step 1: 计算 DCG（Discounted Cumulative Gain）

对于前 k 个推荐结果，DCG 的定义如下：
公式一（使用等级评分）：
$$DCG@k=\sum _{i=1}^k\frac{re{l}_i}{{\log }_2(i+1)}$$
公式二（使用指数评分，更重视高相关性）：
$$DCG@k=\sum _{i=1}^k\frac{2^{re{l}_i}-1}{{\log }_2(i+1)}$$
其中：

• rel_i：第 i 个位置的真实相关性评分（如：点击=1，未点击=0，或等级评分1~5）
• i：排序位置，从 1 开始

Step 2: 计算 IDCG（Ideal DCG）

IDCG 是将相关性从高到低理想排序后得到的 DCG，即最优情况下的 DCG：
$$IDCG@k=\text{DCG@k of ideal (sorted) list}$$

Step 3: 计算 NDCG（归一化 DCG）

$$NDCG@k=\frac{DCG@k}{IDCG@k}$$
如果 IDCG@k = 0（全是 0 分相关性），通常设定 NDCG@k = 0。

示例

直接看公式可能不够清晰，搞个例子。假设模型返回的文档真实相关性为：

predicted ranking:  [D1, D2, D3, D4, D5]
rel_scores:         [3, 2, 3, 0, 1]   ← rel_i

计算 DCG@5（使用公式二）：

DCG@5 = (2^3 - 1)/log2(1+1) + (2^2 - 1)/log2(2+1) + 
        (2^3 - 1)/log2(3+1) + (2^0 - 1)/log2(4+1) +
        (2^1 - 1)/log2(5+1)
      ≈ 7/1 + 3/1.5849 + 7/2 + 0/2.3219 + 1/2.5849
      ≈ 7 + 1.892 + 3.5 + 0 + 0.387
      ≈ 12.779

理想排序的相关性：[3, 3, 2, 1, 0]，计算 IDCG@5（同样方法）：

IDCG@5 ≈ 7/1 + 7/1.5849 + 3/2 + 1/2.3219 + 0/2.5849
       ≈ 7 + 4.417 + 1.5 + 0.430 + 0
       ≈ 13.347

根据Step3

NDCG@5 = 12.779 / 13.347 ≈ 0.957