POJ 3076 / ZOJ 3122 Sudoku（DLX）

Description

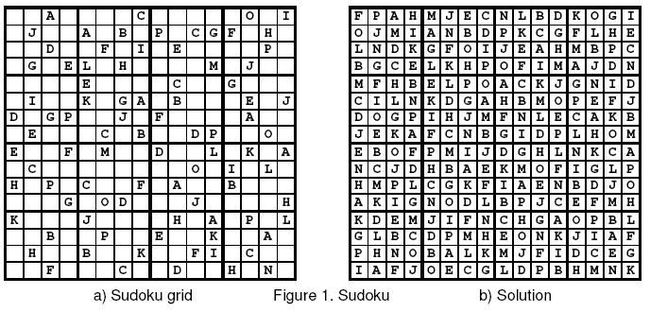
A Sudoku grid is a 16x16 grid of cells grouped in sixteen 4x4 squares, where some cells are filled with letters from A to P (the first 16 capital letters of the English alphabet), as shown in figure 1a. The game is to fill all the empty grid cells with letters from A to P such that each letter from the grid occurs once only in the line, the column, and the 4x4 square it occupies. The initial content of the grid satisfies the constraints mentioned above and guarantees a unique solution.   Write a Sudoku playing program that reads data sets from a text file.

Input

Each data set encodes a grid and contains 16 strings on 16 consecutive lines as shown in figure 2. The i-th string stands for the i-th line of the grid, is 16 characters long, and starts from the first position of the line. String characters are from the set {A,B,…,P,-}, where – (minus) designates empty grid cells. The data sets are separated by single empty lines and terminate with an end of file.

Output

The program prints the solution of the input encoded grids in the same format and order as used for input.

 

题目大意：填一个16×16的数独。

思路：套DLX。

 

代码（POJ 641MS / ZOJ 390MS）

  1 #include <cstdio>
  2 #include <cstring>
  3 #include <iostream>
  4 #include <algorithm>
  5 #include <vector>
  6 using namespace std;
  7 
  8 const int MAXC = 1024 + 10;
  9 const int MAXR = 4096 + 10;
 10 const int MAXP = MAXR * 4 + MAXC;
 11 
 12 struct DLX {
 13     int n, sz;//列数，结点总数
 14     int sum[MAXC];//每列拥有的结点数
 15     int row[MAXP], col[MAXP];//结点所在的行和列
 16     int left[MAXP], right[MAXP], up[MAXP], down[MAXP];//十字链表
 17     int ansd, ans[MAXR];
 18 
 19     void init(int nn) {
 20         n = nn;
 21         for(int i = 0; i <= n; ++i) {
 22             up[i] = down[i] = i;
 23             left[i] = i - 1; right[i] = i + 1;
 24         }
 25         right[n] = 0; left[0] = n;
 26         sz = n + 1;
 27         memset(sum, 0, sizeof(sum));
 28     }
 29 
 30     void add_row(int r, vector<int> columns) {
 31         int first = sz;
 32         for(int i = 0, len = columns.size(); i < len; ++i) {
 33             int c = columns[i];
 34             left[sz] = sz - 1; right[sz] = sz + 1; down[sz] = c; up[sz] = up[c];
 35             down[up[c]] = sz; up[c] = sz;
 36             row[sz] = r; col[sz] = c;
 37             ++sum[c]; ++sz;
 38         }
 39         right[sz - 1] = first; left[first] = sz - 1;
 40     }
 41 
 42     void remove(int c) {
 43         left[right[c]] = left[c];
 44         right[left[c]] = right[c];
 45         for(int i = down[c]; i != c; i = down[i])
 46             for(int j = right[i]; j != i; j = right[j]) {
 47                 up[down[j]] = up[j]; down[up[j]] = down[j]; --sum[col[j]];
 48             }
 49     }
 50 
 51     void restore(int c) {
 52         for(int i = up[c]; i != c; i = up[i])
 53             for(int j = left[i]; j != i; j = left[j]) {
 54                 up[down[j]] = j; down[up[j]] = j; ++sum[col[j]];
 55             }
 56         left[right[c]] = c;
 57         right[left[c]] = c;
 58     }
 59 
 60     bool dfs(int d) {
 61         if(right[0] == 0) {
 62             ansd = d;
 63             return true;
 64         }
 65         int c = right[0];
 66         for(int i = right[0]; i != 0; i = right[i]) if(sum[i] < sum[c]) c = i;
 67         remove(c);
 68         for(int i = down[c]; i != c; i = down[i]) {
 69             ans[d] = row[i];
 70             for(int j = right[i]; j != i; j = right[j]) remove(col[j]);
 71             if(dfs(d + 1)) return true;
 72             for(int j = left[i]; j != i; j = left[j]) restore(col[j]);
 73         }
 74         restore(c);
 75         return false;
 76     }
 77 
 78     bool solve(vector<int> &v) {
 79         v.clear();
 80         if(!dfs(0)) return false;
 81         for(int i = 0; i < ansd; ++i) v.push_back(ans[i]);
 82         return true;
 83     }
 84 };
 85 
 86 DLX solver;
 87 
 88 const int SLOT = 0;
 89 const int ROW = 1;
 90 const int COL = 2;
 91 const int SUB = 3;
 92 
 93 inline int encode(int a, int b, int c) {
 94     return a * 256 + b * 16 + c + 1;
 95 }
 96 
 97 void decode(int code, int &a, int &b, int &c) {
 98     --code;
 99     c = code % 16; code /= 16;
100     b = code % 16; code /= 16;
101     a = code;
102 }
103 
104 char puzzle[16][20];
105 
106 bool read() {
107     for(int i = 0; i < 16; ++i)
108         if(scanf("%s", puzzle[i]) == EOF) return false;
109     return true;
110 }
111 
112 int main() {
113     int kase = 0;
114     while(read()) {
115         if(++kase != 1) printf("\n");
116         solver.init(1024);
117         for(int r = 0; r < 16; ++r)
118             for(int c = 0; c < 16; ++c)
119                 for(int v = 0; v < 16; ++v)
120                     if(puzzle[r][c] == '-' || puzzle[r][c] == 'A' + v) {
121                         vector<int> columns;
122                         columns.push_back(encode(SLOT, r, c));
123                         columns.push_back(encode(ROW, r, v));
124                         columns.push_back(encode(COL, c, v));
125                         columns.push_back(encode(SUB, (r/4)*4+c/4, v));
126                         solver.add_row(encode(r, c, v), columns);
127                     }
128         vector<int> ans;
129         solver.solve(ans);
130         for(int i = 0, len = ans.size(); i < len; ++i) {
131             int r, c, v;
132             decode(ans[i], r, c, v);
133             puzzle[r][c] = 'A' + v;
134         }
135         for(int i = 0; i < 16; ++i) printf("%s\n", puzzle[i]);
136     }
137 }

View Code