POJ 3565 Ants(最佳完美匹配)
Description
Young naturalist Bill studies ants in school. His ants feed on plant-louses that live on apple trees. Each ant colony needs its own apple tree to feed itself.
Bill has a map with coordinates of n ant colonies and n apple trees. He knows that ants travel from their colony to their feeding places and back using chemically tagged routes. The routes cannot intersect each other or ants will get confused and get to the wrong colony or tree, thus spurring a war between colonies.
Bill would like to connect each ant colony to a single apple tree so that all n routes are non-intersecting straight lines. In this problem such connection is always possible. Your task is to write a program that finds such connection.
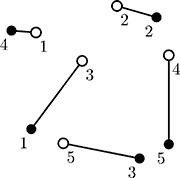
On this picture ant colonies are denoted by empty circles and apple trees are denoted by filled circles. One possible connection is denoted by lines.
Input
The first line of the input file contains a single integer number n (1 ≤ n ≤ 100) — the number of ant colonies and apple trees. It is followed by n lines describing n ant colonies, followed by n lines describing n apple trees. Each ant colony and apple tree is described by a pair of integer coordinates x and y (−10 000 ≤ x, y ≤ 10 000) on a Cartesian plane. All ant colonies and apple trees occupy distinct points on a plane. No three points are on the same line.
Output
Write to the output file n lines with one integer number on each line. The number written on i-th line denotes the number (from 1 to n) of the apple tree that is connected to the i-th ant colony.
题目大意:n个点A和n个点B,每一点A到一点B连一条线,要求n条线互不相交,求一种方案。
思路:可以证明,在费用最小的完美匹配下,所有连线没有相交。这里不证。
PS:WA了几遍才发现平方和最小,和不一定最小……
PS2:跑的是ZKW费用流,我是一个懒人没有改邻接矩阵……
代码(1797MS)(ZKW费用流):

1 //忘删调试语句了…… 2 #include <cstdio> 3 #include <iostream> 4 #include <queue> 5 #include <cmath> 6 #include <cstring> 7 using namespace std; 8 9 const int MAXV = 210; 10 const int MAXE = MAXV * MAXV; 11 const double INF = 1e100; 12 const double EPS = 1e-8; 13 14 inline int sgn(double x) { 15 return (x > EPS) - (x < -EPS); 16 } 17 18 struct ZWK_FLOW { 19 int head[MAXV]; 20 double dis[MAXV]; 21 int next[MAXE], to[MAXE], cap[MAXE]; 22 double cost[MAXE]; 23 int st, ed, ecnt, n; 24 25 void init() { 26 memset(head, 0, sizeof(head)); 27 ecnt = 2; 28 } 29 30 void add_edge(int u, int v, int c, double w) { 31 to[ecnt] = v; cap[ecnt] = c; cost[ecnt] = w; next[ecnt] = head[u]; head[u] = ecnt++; 32 to[ecnt] = u; cap[ecnt] = 0; cost[ecnt] = -w; next[ecnt] = head[v]; head[v] = ecnt++; 33 //printf("%d %d %f\n", u, v - 5, w); 34 } 35 36 void SPFA() { 37 for(int i = 1; i <= n; ++i) dis[i] = INF; 38 priority_queue<pair<double, int> > que; 39 dis[st] = 0; 40 que.push(make_pair(0, st)); 41 while(!que.empty()) { 42 int u = que.top().second; double d = -que.top().first; que.pop(); 43 if(sgn(d - dis[u]) != 0) continue; 44 for(int p = head[u]; p; p = next[p]) { 45 int &v = to[p]; 46 if(cap[p] && sgn(dis[v] - d - cost[p]) > 0) { 47 dis[v] = d + cost[p]; 48 que.push(make_pair(-dis[v], v)); 49 } 50 } 51 } 52 for(int i = 1; i <= n; ++i) dis[i] = dis[ed] - dis[i]; 53 } 54 55 double minCost; 56 int maxFlow; 57 bool use[MAXV]; 58 59 int add_flow(int u, int aug) { 60 if(u == ed) { 61 maxFlow += aug; 62 minCost += dis[st] * aug; 63 return aug; 64 } 65 use[u] = true; 66 int now = aug; 67 for(int p = head[u]; p; p = next[p]) { 68 int &v = to[p]; 69 if(cap[p] && !use[v] && sgn(dis[u] - dis[v] - cost[p]) == 0) { 70 int t = add_flow(v, min(now, cap[p])); 71 cap[p] -= t; 72 cap[p ^ 1] += t; 73 now -= t; 74 if(!now) break; 75 } 76 } 77 return aug - now; 78 } 79 80 bool modify_label() { 81 double d = INF; 82 for(int u = 1; u <= n; ++u) if(use[u]) 83 for(int p = head[u]; p; p = next[p]) { 84 int &v = to[p]; 85 if(cap[p] && !use[v]) d = min(d, dis[v] + cost[p] - dis[u]); 86 } 87 if(sgn(INF - d) == 0) return false; 88 for(int i = 1; i <= n; ++i) if(use[i]) dis[i] += d; 89 return true; 90 } 91 92 double min_cost_flow(int ss, int tt, int nn) { 93 st = ss, ed = tt, n = nn; 94 minCost = maxFlow = 0; 95 SPFA(); 96 while(true) { 97 while(true) { 98 for(int i = 1; i <= n; ++i) use[i] = 0; 99 if(!add_flow(st, 0x7fffffff)) break; 100 } 101 if(!modify_label()) break; 102 } 103 return minCost; 104 } 105 106 void output(int n) { 107 for(int i = 1; i <= n; ++i) { 108 for(int p = head[i]; p; p = next[p]) { 109 int &v = to[p]; 110 if(!cap[p]) {printf("%d\n", v - n); break;} 111 } 112 } 113 } 114 } G; 115 116 struct Point { 117 int x, y; 118 Point() {} 119 Point(int x, int y): x(x), y(y) {} 120 void read() { 121 scanf("%d%d", &x, &y); 122 } 123 Point operator - (const Point &rhs) const { 124 return Point(x - rhs.x, y - rhs.y); 125 } 126 double operator * (const Point &rhs) const { 127 Point a(*this - rhs); 128 return sqrt(a.x * a.x + a.y * a.y); 129 } 130 }; 131 132 Point p[MAXV]; 133 int n; 134 135 int main() { 136 bool flag = true; 137 while(scanf("%d", &n) != EOF) { 138 if(flag) flag = false; else puts(""); 139 for(int i = 1; i <= 2 * n; ++i) p[i].read(); 140 G.init(); 141 for(int i = 1; i <= n; ++i) { 142 for(int j = n + 1; j <= 2 * n; ++j) G.add_edge(i, j, 1, p[i] * p[j]); 143 } 144 int ss = 2 * n + 1, tt = 2 * n + 2; 145 for(int i = 1; i <= n; ++i) G.add_edge(ss, i, 1, 0); 146 for(int i = n + 1; i <= n + n; ++i) G.add_edge(i, tt, 1, 0); 147 G.min_cost_flow(ss, tt, tt); 148 //printf("%d\n", x); 149 G.output(n); 150 } 151 }
代码(94MS)(顺便用一下KM算法):

1 //囧,KM都写了顺便改一下吧 2 #include <cstdio> 3 #include <cctype> 4 #include <cstring> 5 #include <algorithm> 6 #include <cmath> 7 using namespace std; 8 9 const int MAXN = 110; 10 const double INF = 1e100; 11 const double EPS = 1e-8; 12 13 inline int sgn(double x) { 14 return (x > EPS) - (x < -EPS); 15 } 16 17 int n; 18 double mat[MAXN][MAXN], slack[MAXN], Lx[MAXN], Ly[MAXN]; 19 int left[MAXN]; 20 bool S[MAXN], T[MAXN]; 21 22 bool dfs(int i) { 23 S[i] = true; 24 for(int j = 1; j <= n; ++j) if(!T[j]) { 25 double t = Lx[i] + Ly[j] - mat[i][j]; 26 if(sgn(t) == 0){ 27 T[j] = true; 28 if(!left[j] || dfs(left[j])){ 29 left[j] = i; 30 return true; 31 } 32 } 33 else slack[j] = min(slack[j],t); 34 } 35 return false; 36 } 37 38 void update() { 39 double a = INF; 40 for(int i = 1; i <= n; ++i) if(!T[i]) 41 a = min(slack[i],a); 42 for(int i = 1; i <= n; ++i){ 43 if(S[i]) Lx[i] -= a; 44 if(T[i]) Ly[i] += a; else slack[i] -= a; 45 } 46 } 47 48 void KM() { 49 for(int i = 1; i <= n; ++i) { 50 Lx[i] = Ly[i] = left[i] = 0; 51 for(int j = 1; j <= n; ++j) Lx[i] = max(Lx[i], mat[i][j]); 52 } 53 for(int i = 1; i <= n; ++i) { 54 for(int j = 1; j <= n; ++j) slack[j] = INF; 55 while(true){ 56 for(int j = 1; j <= n; ++j) S[j] = T[j] = 0; 57 if(dfs(i)) break; else update(); 58 } 59 } 60 //int ans = 0; 61 //for(int i = 1; i <=n; ++i) ans += Lx[i] + Ly[i]; 62 //return ans; 63 } 64 65 void output() { 66 for(int i = 1; i <= n; ++i) printf("%d\n", left[i]); 67 } 68 69 struct Point { 70 int x, y; 71 Point() {} 72 Point(int x, int y): x(x), y(y) {} 73 void read() { 74 scanf("%d%d", &x, &y); 75 } 76 Point operator - (const Point &rhs) const { 77 return Point(x - rhs.x, y - rhs.y); 78 } 79 double operator * (const Point &rhs) const { 80 Point a(*this - rhs); 81 return sqrt(a.x * a.x + a.y * a.y); 82 } 83 }; 84 85 Point p1[MAXN], p2[MAXN]; 86 87 int main() { 88 bool flag = true; 89 while(scanf("%d", &n) != EOF) { 90 if(flag) flag = false; else puts(""); 91 for(int i = 1; i <= n; ++i) p1[i].read(); 92 for(int i = 1; i <= n; ++i) p2[i].read(); 93 for(int i = 1; i <= n; ++i) { 94 for(int j = 1; j <= n; ++j) mat[j][i] = -(p1[i] * p2[j]); 95 } 96 KM(); 97 output(); 98 } 99 }
