人工智能——Petri网表示法

Petri网是由德国学者Cah Abam Petri于1962年在其博士论文“Communication with Automata”提出来的，用于构造系统模型及进行动态特性分析。

 

1. Petri网表示法

Petri网模型3种基本元素：位置集P（Place Set）、转换集T（Transition Set）及标记集M（Marker Set或Token Set）。三元组模型

 

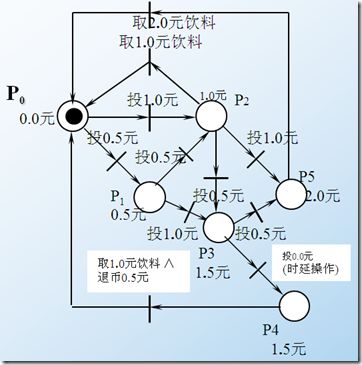
有一种饮料自动机，可销售1.0元或2.0元两种瓶装饮料。该系统可接收面值为0.5和1元的两种硬币，且销售机存储硬币的最大容量为2.0元。

1) 使用三元组模型来表示该系统，即

P表示价位状态节点集；

T表示转换操作集（包括投币、取货、退币、时延等独立或联合操作），

M表示标记集，销售机工作状态之间的变迁，用带箭头的有向弧线加以联结来标记。

2) 使用Petri网建立该瓶装饮料自动销售机系统模型

图1饮料自动销售机的Petri网模型

 

对于复杂的系统或知识，Petri网用一个八元组来表示知识间的因果关系，形式为

P：位置的有限集

T：转换的有限集

D：命题的有限集

I：输入函数，表示从位置到转换的映射

O：输出函数，表示从转换到位置的映射

f：相关函数，表示强度，0-1之间

：相关函数，表示位置对应命题的可信度，0-1之间

：相关函数，表示位置到命题的映射，位置对应的命题

 

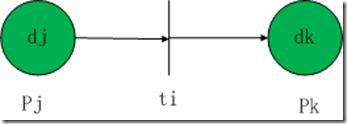
IF d_j THEN d_k （CF=ui），若dj的可信度为0.8，规则强度ui=0.9

图2 Petri网表示例示

 

P={Pj，Pk}

T={ti}

D={dj，dk}

I(ti)={Pj}

O(ti)={Pk}

f(ti)=ui=0.9

(Pj)=0.8

(Pj)=dj (Pk)=dk

 

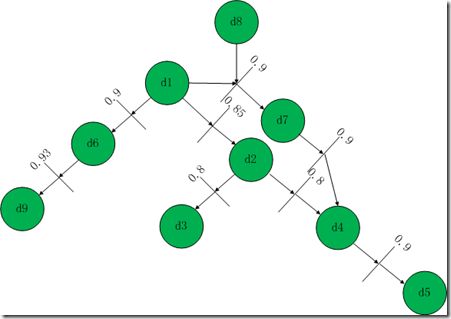
产生式规则集为：

R1: IF d1 THEN d2 (cf=0.85)

R2: IF d2 THEN d3 (cf=0.8)

R3: IF d2 THEN d4 (cf=0.8)

R4: IF d4 THEN d5 (cf=0.9)

R5: IF d1 THEN d6 (cf=0.9)

R6: IF d6 THEN d9 (cf=0.93)

R7: IF d1 AND d8 THEN d7 (cf=0.9)

R8: IF d7 THEN d4 (cf=0.9)

图3 Petri网表示例示

 

2. Petri网表示法的特点

1) 便于描述系统状态的变化及对系统特性进行分析

2) 可以在不同层次上变换描述

 

参考文献：

[1] 王永庆. 人工智能原理与方法. 西安: 西安交通大学出版社

[2] 尹朝庆. 人工智能方法与应用. 武汉: 华中科技大学出版社, 2007.