HDU 4116 Fruit Ninja （ 计算几何 + 扫描线 ）

给你最多1000个圆，问画一条直线最多能与几个圆相交，相切也算。

显然临界条件是这条线是某两圆的公切线，最容易想到的就是每两两圆求出所有公切线，暴力判断一下。

可惜圆有1000个，时间复杂度太高。

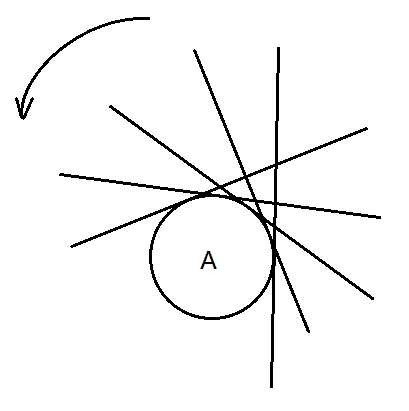
网上题解的做法是枚举每个“中心圆”，求出这个圆与其他圆的切线，然后按极角排序，扫一圈。

把每条切线看成扫入线——添加一个圆，或扫出线——删除一个圆。

形象一点就是一条与中心圆相切的直线，沿着中心圆滚了一圈，当这个直线碰到其他圆时，是添加了一个圆还是删除了一个圆。

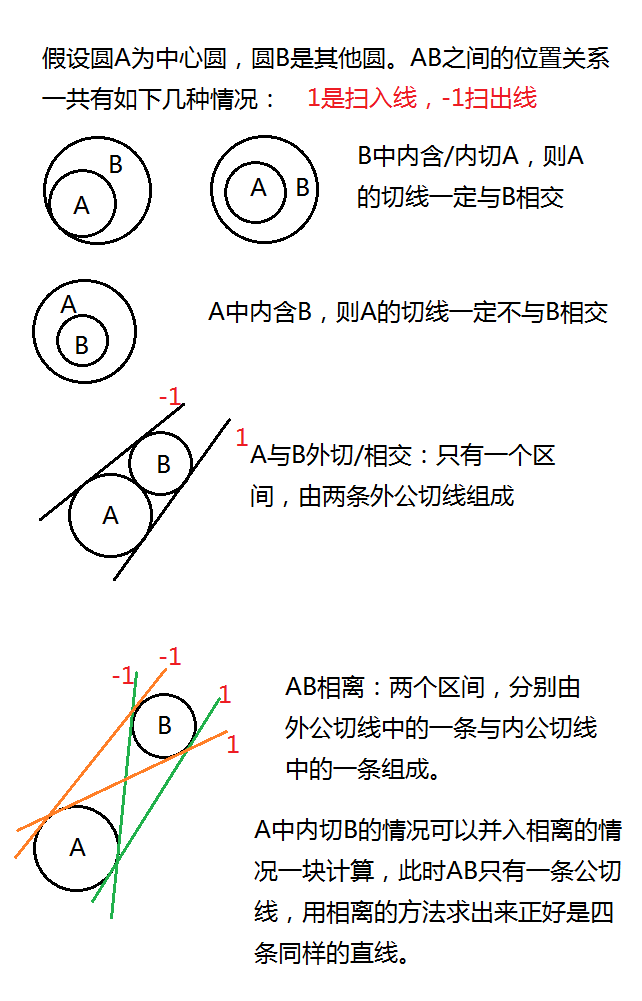
PS:这题C++交死活TLE，G++才能交过。为什么为什么为什么orz……

PS2:这题我之前少判了一种情况（就是那个A内含B的情况），导致fix调整角度区间的时候进了死循环好像，然后TLE了很长时间，去掉fix之后又RE。然后我就来回注释这附近的代码交上去各种测，错使我在错误的地方调错调了很长时间。实际上只是因为没有把那种情况判出去，导致后面的运算非法。以后要多注意这种情况。

PS3：感觉这题还有很多细节，但是我说不清楚了，直接看代码吧……

#include <cstdio>

#include <cstring>

#include <cstdlib>

#include <cmath>

#include <algorithm>



using namespace std;



const int MAXN = 10100;

const double eps = 1e-9;

const double PI = acos( -1.0 );



struct Point

{

    double x, y;

    Point( double x = 0, double y = 0 ):x(x), y(y) { }

    void readPoint()

    {

        scanf( "%lf%lf", &x, &y );

        return;

    }

};



int dcmp( double x )    //控制精度

{

    if ( fabs(x) < eps ) return 0;

    else return x < 0 ? -1 : 1;

}



double PointDis( Point a, Point b )

{

    return sqrt( (a.x-b.x)*(a.x-b.x) + (a.y-b.y)*(a.y-b.y) );

}



//调整到0~2*PI区间

double fix( double ang )

{

    while ( dcmp( ang ) < 0 ) ang += 2.0*PI;

    while ( dcmp( ang - PI - PI ) >= 0 ) ang -= 2.0*PI;

    return ang;

}



struct Line

{

    int id;       //哪个圆的切线

    int s;        //扫入扫出线

    double ang;   //极角

    Line() { }

    Line( int id, int s, double ang ): id(id), s(s), ang(ang) { }

};



bool cmp( const Line& lhs, const Line& rhs )

{

    int tmp = dcmp( lhs.ang - rhs.ang );

    if ( tmp ) return tmp < 0;

    else return lhs.s > rhs.s;

}



struct Circle

{

    Point c;   //圆心坐标

    double r;  //半径

    Circle() {}

    Circle( Point c, double r ): c(c), r(r) {}

    Point getPoint( double theta )   //根据极角返回圆上一点的坐标

    {

        return Point( c.x + cos(theta)*r, c.y + sin(theta)*r );

    }

    void readCircle()

    {

        scanf("%lf%lf%lf", &c.x, &c.y, &r );

        return;

    }

};



//获得切线的斜率

void GetTangent( Circle& A, Circle& B, int& id, int& sum, int& LineN, Line *L )

{

    double dis = PointDis( A.c, B.c );

    double base = atan2( B.c.y - A.c.y, B.c.x - A.c.x );



    //A内含B

    if ( dcmp( A.r - B.r - dis ) > 0 ) return;



    //B内含+内切A

    if ( dcmp( B.r - A.r - dis ) >= 0 )

    {

        ++sum;

        return;

    }

/*

    //A内切B

    if ( dcmp( A.r - B.r ) > 0 && dcmp( dis - rdiff ) == 0 )

    {

        L[LineN++] = Line( id,  1, base - PI/2 - eps );

        L[LineN++] = Line( id, -1, base - PI/2 + eps );

        return;

    }

*/

    //外切+相交

    double ang1 = asin( (B.r - A.r) / dis );

    double ang2 = asin( (A.r + B.r) / dis );

    if ( dcmp( A.r + B.r - dis ) >= 0 )

    {

        L[LineN++] = Line( id,  1,  fix( base - ang1 ) );

        L[LineN++] = Line( id, -1,  fix( base + ang1 + PI ) );

        return;

    }



    //相离

    L[LineN++] = Line( id,  1, fix( base - ang1 ) );

    L[LineN++] = Line( id, -1, fix( base + ang2 ) );

    L[LineN++] = Line( id,  1, fix( base - ang2 + PI ) );

    L[LineN++] = Line( id, -1, fix( base + ang1 + PI ) );



    return;

}



bool vis[MAXN];

int solved( int cN, int LineN, Line *L )

{

    int res = 0;

    int sum = 0;



    memset( vis, false, sizeof(bool)*(cN+4) );



    for ( int i = 0; i < LineN + LineN; ++i )

    {

        int k = i % LineN;

        int id = L[k].id;

        int s = L[k].s;



        if ( s == 1 )

        {

            if ( !vis[id] )

            {

                vis[id] = true;

                ++sum;

            }

        }

        else

        {

            if ( vis[id] )

            {

                vis[id] = false;

                --sum;

            }

        }

        if ( sum > res ) res = sum;

    }

    return res;

}



Line L[MAXN << 2];

Circle cc[MAXN];

int cN;



int main()

{

    //freopen( "in.txt", "r", stdin );

    //freopen( "out.txt", "w", stdout );

    int T, cas = 0;

    scanf( "%d", &T );

    while ( T-- )

    {

        scanf( "%d", &cN );

        for ( int i = 0; i < cN; ++i )

            cc[i].readCircle();



        int ans = 0;

        for ( int i = 0; i < cN; ++i )

        {

            int sum = 1;

            int LineN = 0;

            for ( int j = 0; j < cN; ++j )

            {

                if ( i == j ) continue;

                GetTangent( cc[i], cc[j], j, sum, LineN, L );

            }



            sort( L, L + LineN, cmp );

            sum += solved( cN, LineN, L );

            if ( sum > ans ) ans = sum;

        }



        printf( "Case #%d: %d\n", ++cas, ans);

    }

    return 0;

}