数学之路(3)-机器学习(3)-机器学习算法-欧氏距离(5)
一个随机变量的方差描述的是它的离散程度,也就是该变量离其期望值的距离。一个实随机变量的方差也称为它的二阶矩或二阶中心动差,恰巧也是它的二阶累积量。方差的算术平方根称为该随机变量的标准差。方差和标准差是测度数据变异程度的最重要、最常用的指标。
设总体方差为σ2,对于未经分组整理的原始数据,方差的计算公式为:

方差反映了变量与均值之间的偏离程度,当方差较大时,说明变量之间差异较大,分布相对分散,否则分布相对集中,且变量之间差异不大。
本博客所有内容是原创,如果转载请注明来源
http://blog.csdn.net/myhaspl/
传统的欧式距离存在一定的弊端,对所有的像素点给予一样的权重,图像经过灰度化后,强化了人脸本身的图像,弱化了背景,但一些小的像素差异仍可能引起对结果的判断。因为少数像素点之间的差异过大,造成欧式距离失真得放大,我们可以引入另外一个权重,对欧式距离进行整体调整。我们可以引入统计学上的方差。
如果使用传统的欧式距离,将产生下面的错误匹配结果:
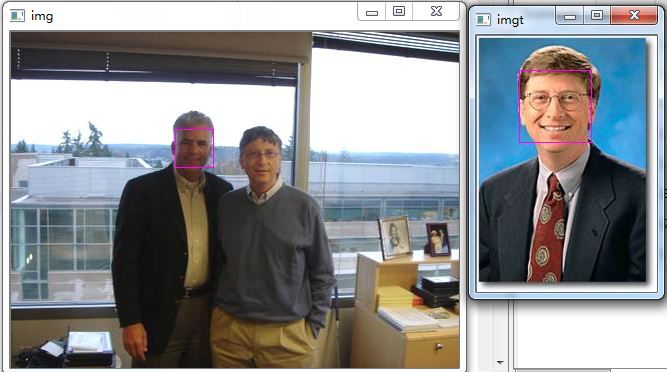
引入方差后,匹配精度更高,成功在图片中找到了BillGates~
运行修改后程序
>>> runfile(r'K:\book_prog\ann_facesbtest.py', wdir=r'K:\book_prog')
http://blog.csdn.net/myhaspl
[email protected]
loading ...
>>>
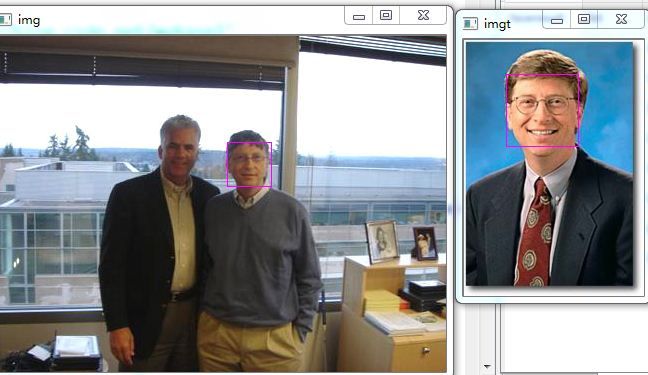
部分代码如下:
fn='billall2.png'
fnt='billtest.png'
my_img=cv.LoadImage(fn)
face_test=cv.LoadImage(fnt)
#获取脸在图片中的坐标
faceresult=findface(my_img)
facet_result=findface(face_test)
myimg=cv2.imread(fn)
myimgt=cv2.imread(fnt)
#IT精英比尔盖茨
isface1=get_distance(myimg[faceresult[0][0][0]:faceresult[0][1][0],faceresult[0][0][1]:faceresult[0][1][1],:],myimgt[facet_result[0][0][0]:facet_result[0][1][0],facet_result[0][0][1]:facet_result[0][1][1],:])
isface2=get_distance(myimg[faceresult[1][0][0]:faceresult[1][1][0],faceresult[1][0][1]:faceresult[1][1][1],:],myimgt[facet_result[0][0][0]:facet_result[0][1][0],facet_result[0][0][1]:facet_result[0][1][1],:])
if isface1<isface2:
cv2.rectangle(myimg, faceresult[0][0], faceresult[0][1],(255,0,255))
cv2.rectangle(myimgt, facet_result[0][0], facet_result[0][1],(255,0,255))
else:
cv2.rectangle(myimg, faceresult[1][0], faceresult[1][1],(255,0,255))
cv2.rectangle(myimgt, facet_result[0][0], facet_result[0][1],(255,0,255))
cv2.namedWindow('img')
cv2.imshow('img', myimg)
cv2.namedWindow('imgt')
cv2.imshow('imgt', myimgt)
cv2.waitKey()
cv2.destroyAllWindows()