KMP
目的:本博客以KMP算法为载体,试图在减少思维断层情况下学习作者算法思想。
目录:
1)开脑之字符匹配思路
2)浅析回溯目的
3)一定要回溯吗
4)什么时候回溯?什么时候不回溯?
5)深入回溯目的
6)如何更为高效地回溯?
7)回溯到哪一步?
8)前缀和后缀应运而生!
9)你猜我发现什么?一切的一切都是因为这个(关键步骤)
10)KMP就是这样
第一步:开脑之字符匹配
字符匹配问题是指:在一个目标字符串(如a b a b a b a a b a b …)中寻找模式字符串(如a b a b a c b)的问题,很多复杂的问题最终都可以抽象成字符串匹配问题。
最简单的办法:像上图一样,当第一次匹配b和c匹配失败时,将模式串简单的向后移动一个字符。最终在n=8次的匹配之后,终于来到了目标串中的第5个a面前,此次一举成功,整个过程可谓艰辛。
第二步:浅析回溯目的
上述步骤有什么不对吗?有。
问题就出在:不管模式串是什么比如abab或者diekd抑或wwwww,该方法都能够解决问题,这是一个万能方法。
万能方法实际上意味着没有抓住不同事物具有不同的特性,将所有的事情一律平等待之。这个也许有助于社会和谐,但也就意味着会丧失很多不同的人有自己的特殊之处这样的特点。
算法不只是追求解决问题,更主要是追求高效。
该方法为什么如此低效,大家肯定都明白,就是这个万能方法将所有的问题平等待之。
找到平等待之之处,试着改变其策略。
上述问题是如何实现平等待之的呢?回溯!
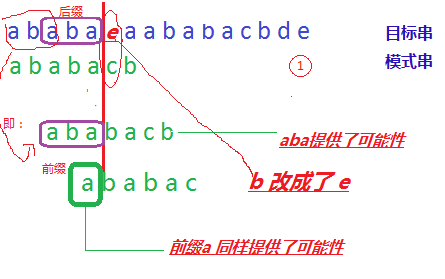
所谓回溯是指:当某一次匹配如第一次,当匹配到了第6个字符的时候,发现b和c是不同的,此时我们将指示目标串的指针i(此时指向了6)回溯到i=2,并从模式串的第1个字符开始重新匹配。
这样做有什么作用呢?显然,这样做是因为第3个字符同样是a,和模式串的首字母a相同,为匹配成功提供了可能性。
第三步:一定要回溯吗?
如果已经匹配正确的前5个字符ababa中只有第1个字符是a,而其他字符都不是a,这样就完全没有提供匹配成功的可能性了。
例如匹配目标串abcdef而模式串是abcdeg,同样当比较第6个字符f和g时出现不同,此时还有必要回溯吗?显然没有,因为第2-5个字符bcde中根本就没有a。
第四步:什么时候回溯?什么时候不回溯?
一个显而易见的结论是:当匹配失败的字符前面(除了开始的字符)有和模式串中相同首字母(本例子为a)的时候,就有匹配成功的可能性,就有回溯的必要性;相反,则没有回溯的必要性。
第五步:深入回溯目的
回溯的目的其实就是找到所有的匹配成功的可能性例如第一步中第6个字符b和c匹配的时候,匹配失败,本例中,前5个字符中(ababa)除了首字母a外还有2个a,这两个a都提供了匹配成功的可能性(当然,并不能只是因为有a就回溯,想要更加高效的回溯,需要仔细分析其特性)。
但是,朴素算法的回溯,只是简单的一个一个递增的回溯,并没有利用前5个字符已经成功匹配的事实。你无法忽视这个事实,你也不能忽视这个事实,这就是普通匹配算法低效的原因。
第六步:如何更为高效地回溯?
再看本案例:

上述有4步,用数字1,2,3,4表示出来了。显然,我们已经知道第2步没有必要进行,那第3步有必要进行吗?实际上就是回溯到哪一步,如何高效地回溯的问题,即效率问题。
如何判断回溯到哪一步?
什么时候回溯和什么时候不回溯实际上也是回溯到哪一步的问题,即解决此问题实际上也就解决了第四步的问题。
现在所有的问题就转化成了回溯到哪一步的问题。
第七步:回溯到哪一步?
关于回溯到哪一步,直观感受是:匹配失败字符前面,有几个a就进行几次回溯。本例中,前5个字符中(ababa)除了首字母a外还有2个a,这两个a都提供了匹配成功的可能性。所以,按道理来讲需要回溯两次。
这样效率确实提高了很多,起码在普通匹配算法中需要匹配4次的情况下,变成了匹配两次,有的时候还不止这样,可能更为高效。
也许你已经看出来了,这种做法有点不太科学或者说还是不够高效?原因在于我们只是根据首字母来判定是不是有回溯的必要。
既然有了好的思路,何不再仔细分析模式串,然后走的更远些。
第八步:前缀和后缀应运而生!
上面我们已经确定第二步没有必要进行,因为两个首字母(b和a)就不同(一票否决)。
第3步有必要吗?
第3步中,我们比较了第1个字符(首字符)a相同之后,再比较第2个字符b发现相同,再比较第三个字符a发现还是相同,于是我们断定此次进行回溯是有可能是有必要的。
插入一个知识点:前后缀
前缀:
a是abcdtyd的前缀,ab是abcdtyd的前缀,abc是abcdtyd的前缀
后缀:
d是abcdtyd的后缀;yd是abcdtyd的后缀;tyd是abcdtyd的后缀
再仔细观察:
发现:aba即使已经匹配的字符ababa的前缀,同时又是其后缀。而且还不止这些,aba是字符串ababa中,保证前缀等于后缀的前提下,aba是最大的前缀(也是最大后缀)。
解决第七步的实质问题是:前后缀问题,即找到前缀等于后缀,并且是最大的.(如果还有疑惑可以自行举例试一试)
第九步:你猜我发现什么?一切的一切都是因为这个(关键步骤)
前后缀,提供了成功匹配的可能性,是判断是否有要回溯的必要的依据。但是这个还不够。
现在我们具体分析一下。
当第6个字符b和c匹配失败的时候,前5个字符是ababa。其实,并不只是只有最大的前缀=后缀即aba提供匹配成功的可能性。
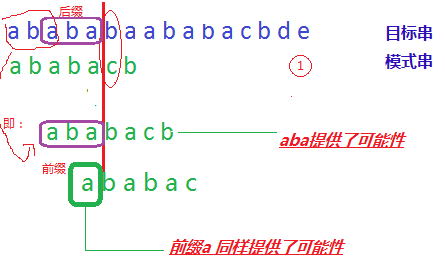
这个图意味着:对于匹配失败的字符(第6个)前面的字符串的所有的前缀同样也是后缀的子字符串例如本例中aba和a。提供了匹配成功的可能性。至于是否能够匹配成功,本例中aba匹配的时候,下一个字符是b和目标串中的第6个字符相同,说明匹配成功指示目标串和模式串的指针继续往前走。
但是如果aba的后一个字符和目标串的第6个字符匹配失败,例如:
此次aba的下一个字符b和e匹配失败,我们就需要检查前缀a的下一个字符是否满足。
如果此次字符很少,也就5个,可能分析起来不具有代表性,我们增加字符的个数。
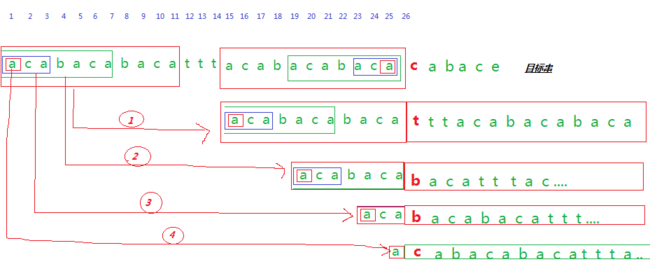
在匹配第26个字符c和f的时候,匹配失败。
下面我们分析前25个已经匹配成功的字符。
用图片表示
前3次匹配都没有成功,分别向后移动了14、18和22个字符。
发现第4次匹配时,a之后的c和第26个字符c相同,此时模式串已经向后移动了24个字符,即目标串的第26个字符和模式串的第2个字符串比较。
如果你已经看懂了上述过程:下面介绍KMP算法所有的一切的根本属性
上述4对符合条件的前缀有如下性质:
如果你看过KMP代码,同时发现有两段代码尤为相似的话,其实并不用惊奇。因为不论是KMP算法中调用Next数组,还是计算Next数组,决定这最为关键的特别相似的两步的东西就是这个属性。当然这是后话。
第十步:KMP就是这样
在进行匹配的时候,我们定义两个指针i和j分别指向目标串和模式串,起始值为1。
上述例子中,当i和j同时指向26的时候,i指向了c,而j指向的是f,出现两者比匹配。此时才有了后来的4次前缀匹配比较。
第1次第一大前缀s1:acabacabaca 以t和i指向的c不匹配的失败告终。实际上相当于将j = 26改变成j= 12 ,i还是26继续比较。
第2次第二大前缀s2:acabaca 以b 和i指向的c不匹配的失败告终。实际上相当于将j = 12 改变成 j =8 ,i还是26继续比较。
直到第4次第四大前缀s4:a 以c和i指向的c匹配的成功告终。实际上相当于将j = 4 改变成j =2 ,i还是26继续比较。
上述过程的实质是:i=26并不改变,只是不断改变j的值。
但是当i=26发现匹配失败,然后决定改变j的值,而这个值是根据前面已经匹配的25个字符得出来的,跟目标串没有任何关系。
如果定义一个数组next,当第j个字符和目标串中第i个字符发生步匹配的时候,只需要查询next[j]就可以得到将j改变成的值。
Next[j]表示的是:当第j个字符匹配失败时,得到前j-1个字符的最大前缀+1.
上例中:假设已经得到了next数组
开始I = 26,j = 26.发生不匹配。
1)查询next[26]可以得到12,其实12是第一大前缀s1 的大小(11)+1得到。比较j = 12时,字符为t ,发现还是与I = 26 字符为c不等。下一步怎么办?
2)当然是进行第2步,将j改为8 ,其实8是第二大前缀s2的大小(7)+1得到。比较j = 8时,字符为b ,发现i= 26字符为c不等。
那么到底是如何计算将j 改成了8呢?当然是next[12],因为这一步相当于是i=26,j=12时匹配失败,此时调用next[12]得到需要价将j改变成的值。
这实际用到上述的根本属性
第2大前缀s2是第1大前缀s1的最大前缀。
根据next的定义Next[12] = 7+1 = 8 存放的是前11个字符(即s1)的最大前缀(即s2)+1。
上面是在得到next数组的基础上计算的,那么下一步就是如何得到这个next数组呢?
举例:
上例中,第一步计算时用到的next[26] = 12是怎么来的?
假设我们已经知道了next[25] 即知道前24个字符的最大前缀+1的值。
从上图中可以看出前24个字符最大前缀是acabacabac 大小为10
下一步:
比较第11个字符a 和第25字符a是否相同
本例中相同,则next[26]=next[25]+1=11+1 = 12 即前25个字符最大前缀+1=12
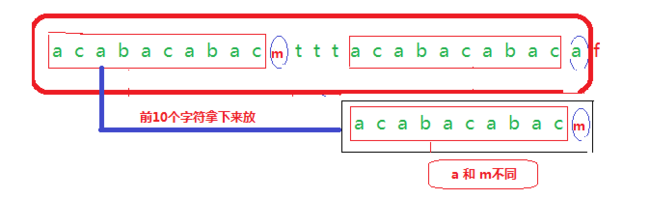
如果不相同呢?我们将第11个字符改成m,如下图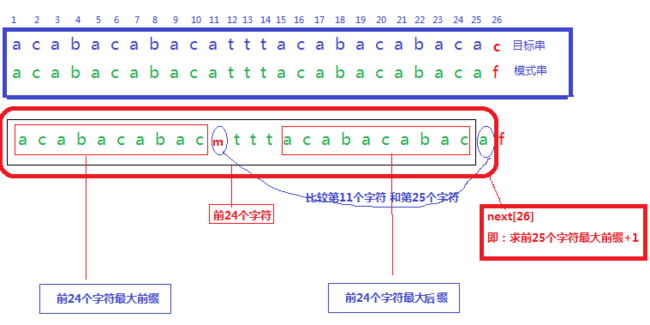
此时前25个字符最大前缀+1 等于???
而已知条件是next[25] =11 即前24个字符最大前缀大小是10.
这样和我们本来要解决的问题当第i=26 ,j=26时,字符不匹配。只是这次i变成了I =25 , j=11 。那么前25个字符的最大前缀怎么求呢?当然是将j改成前10个字符的最大前缀+1,实际上用next表示就是next[11](11就是此时的j),然后再判断此时i和j对应的字符是否相同。
j一直再减小,有可能最后都没有办法匹配。如abcdef 求next[6]但是前几个字符都没有能找到最大前缀=后缀的,此时next[6] =0+1 = 1.
所以已知next[j]的时候,想要求next[j+1],有两种情况(设模式串为P)
1)如果P(next[j]) == P(j+1) 则next[j+1] = next[j]+1
2)如果P(next[j]) != P(j+1) 则比较P(next[next[j]]) 和P(j+1) 如果还是不等,继续比较。直到最后没有找到可以成功匹配的,则next[j+1] = 1,如abcdef中next[6]=1表示当第6个字符匹配失败的时候,需要和第1个字符匹配。如果仍旧没有匹配成功,相当于刚开始匹配的时候,第一个字符就不匹配如目标串abcde和模式串bctds ,此时查找next[1] ,因为next[1]的含义就是第1个字符就匹配失败,我们定义为next[1]=0.(其实0只是一个标志,你完全可以定义为-1,-2),只是当j =-1或者-2 的时候,此时需要模式串的第一个字符和目标串的第二个字符开始比较了,即i++,j +=1或者j+=2.(大部分都是用的0当标志,因为这样代码就可以一起判断)
总结:KMP算法确实巧妙,但是不论算法如何巧妙,最终都是在问题性质之上去解决问题。就像贪婪选择的贪婪选择属性和最优子结构和动态规划的重叠子问题和最优子结构一样,一旦你能够找到这些性质,就抓住了其核心、其本质解决起来得心应手。