对弈类游戏的人工智能(3)--博弈树优化
前言:
对弈类游戏的智能算法, 网上资料颇多, 大同小异. 然而书上得来终觉浅, 绝知此事要躬行. 结合了自己的工程实践, 简单汇总整理下. 一方面是对当年的经典<<PC游戏编程(人机博弈)>>表达敬意, 另一方面, 也想对自己当年的游戏编程人生做下回顾.
承接上两篇博文:
(1). 评估函数+博弈树算法
(2). 学习算法
这篇博文回归到博弈树这边, 具体阐述下博弈树的优化手段, 为了游戏性添加的合理技巧.
启发搜索:
博弈树本质是极大极小的求解过程, 而alpha+beta剪枝则加速该求解过程.
让我们来构建一个简单的alpha+beta剪枝用例:
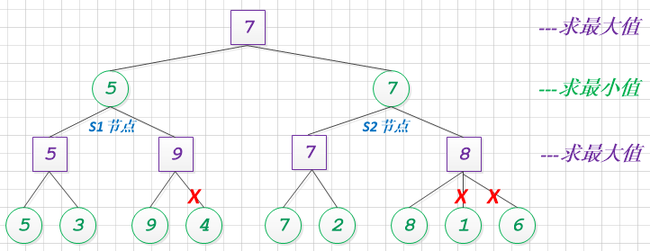
注: 紫色代表极大值求解, 绿色代表极小值求解.
通过人工演算和模拟, 整个博弈过程, 成功地减少了3个节点的计算量的, 效果一般.
这个过程, 我们是否有优化的余地呢? 让我们调整下, 节点S1和S2的搜索顺序.
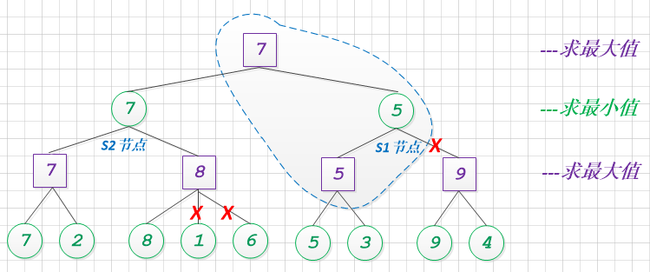
与调整顺序之前相比, 其alpha+beta剪枝的效果提升, 砍去了一个大分支, 减少了4个节点的计算量.
从这个例子中, 我们可以清晰的看到, 对于博弈树而言, 其alpha+beta的剪枝效果, 和搜索顺序是有一定关系的. 简单的总结: alpha+beta效果, 对搜素的顺序敏感.
于是我们找到了一个优化方向: 调整可行步的顺序, 并优先搜索预期高的分支. 该技巧命名为: 启发搜索. 常有人借助历史值, killer步来构造启发函数.
// 负极大值算法
int negamax(GameState S, int depth, int alpha, int beta) {
// 游戏是否结束 || 探索的递归深度是否到边界
if ( gameover(S) || depth == 0 ) {
return evaluation(S);
}
// 依据预估(历史, 经验)对可行步, 进行排序
sort (candidate list);
// 遍历每一个候选步
foreach ( move in candidate list ) {
S' = makemove(S);
value = -negamax(S', depth - 1, -beta, -alpha);
unmakemove(S')
if ( value > alpha ) {
// alpha + beta剪枝点
if ( value >= beta ) {
return beta;
}
alpha = value;
}
}
return alpha;
}
此时的核心算法结构中: 添加了可行步排序过程(sort (candidate list)).
当然该过程是有一定代价的, 在alpha+beta剪枝效果提升和排序损耗需要均衡和折中. 一般采用计算简单的预估函数即可.
让我们回到黑白棋AI, 我们可以简单选定, 预估函数等同于位置表, 即P(x, y) = Map(x, y). (Map 为 黑白棋棋面的位置重要度矩阵), 效果斐然.
置换表:
搞过ACM的人, 都知道DP求解的一种方式: 记忆化搜索. 本质就是把中间状态保存, 减少重复搜索的一种技巧.
置换表的核心思想基本一致: 状态保存, 减少重复搜索.
但置换表的难点不在于思想, 而在于状态保存.
具体可以分析如下:
1). 游戏局面S本身占用空间大, 而且需要保存的状态S集合多, 因此需要一个转换函数F(S) => key, (key为不长二进制串, 或一个很大的整数)
2). 转换后的key, 一一对应了某个具体局面S (冲突率很低可忽略, 或不存在)
让我们以黑白棋来做个例子, 局面转换为矩阵(0: 空白, 1: 黑棋, 2:白棋), 扁平化为字符串, 在借助强有力的Hash函数来转化.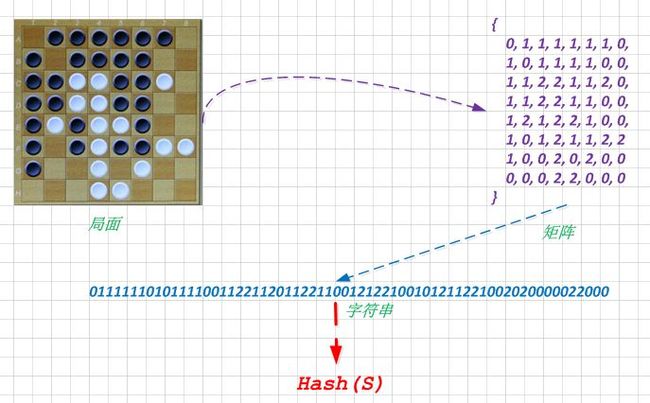
这边展示了具体的流程, 其效果的好坏, 取决于Hash函数的选择.
简单采用MD5算法, 其实是可行的, 不过比较消耗CPU. Zobrist hashing算法也是备受推荐.
和记忆化搜索相比, 置换表对应的局面是, 只是中间的预测节点, 因此该状态除了本身和游戏局面相关, 还和当前的搜索深度有关.
因此具体代码可修正如下:
// 负极大值算法
int negamax(GameState S, int depth, int alpha, int beta) {
// 判断状态已存在于置换表中, 且搜索深度小于等于已知的, 则直接返回
if ( exists(TranspositionTable[S]) && TranspositionTable[S].depth >= depth ) {
return TranspositionTable[S].value
}
// 游戏是否结束 || 探索的递归深度是否到边界
if ( gameover(S) || depth == 0 ) {
return evaluation(S);
}
// 遍历每一个候选步
foreach ( move in candidate list ) {
S' = makemove(S);
value = -negamax(S', depth - 1, -beta, -alpha);
// 保存S'到置换表中, 当depth更深时.
TranspositionTable[S'] <= (depth, value) If TranspositionTable[S'].depth < depth
unmakemove(S')
if ( value > alpha ) {
// alpha + beta剪枝点
if ( value >= beta ) {
return beta;
}
alpha = value;
}
}
return alpha;
}
总结:
启发搜索和置换表, 两者都是很好的思路, 前者通过调整搜索顺序来加速剪枝效果. 后者通过空间换时间. 总而言之, 这些都是博弈树上很常见的优化手段. 当然在具体游戏中, 需要权衡和评估. 下一篇讲讲出于游戏性的考虑, 如何进行优化和策略选择.
写在最后:
如果你觉得这篇文章对你有帮助, 请小小打赏下. 其实我想试试, 看看写博客能否给自己带来一点小小的收益. 无论多少, 都是对楼主一种由衷的肯定.
