Tensor神经网络进行知识库推理

本文是我关于论文《Reasoning With Neural Tensor Networks for Knowledge Base Completion》的学习笔记。

一、算法简介

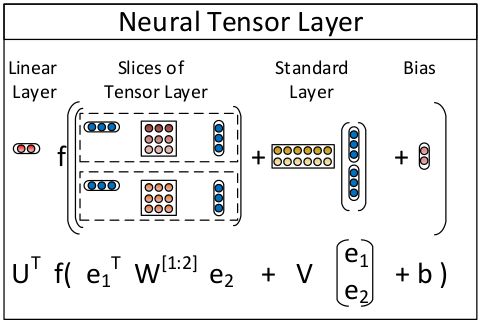
网络的结构为：

$$g(e_1,R,e_2)=u^T_Rf(e_1^TW_R^{[1:k]}e_2+V_R\begin{bmatrix} e_1 \\ e_2 \\ \end{bmatrix}+b_R)~~~~~~~~~~~(1)$$

其中$g$为网络的输出，也即对该关系$R$ 的打分。$e_1$,$e_2$为两个实体的特征向量，维度都为$d$，初始化可以是随机值，也可以是通过第三方工具训练后的向量，在训练中还需不断调整。

右边括号中扣除第一部分（Tensor部分），整个网络就是一典型的三层bp网络。$f=tanh$是隐层激活函数，输出层激活函数为$pureline$，第一层权重为$V$,偏置为$b$,第二层权重为$u$。

右括号第一项为Tensor项。$W_R^{[1:k]}\in R^{d\times d \times k}$是张量，每个$W_R^i$是$d\times d$矩阵，称作一个$slice$，网络中共有$k$个$slice$，对应神经网络隐层节点个数。$h_i=[e_1^TW_R^{[1:k]}e_2]_i=e_1^TW_R^i e_2$。

论文中给出的对应图示为：

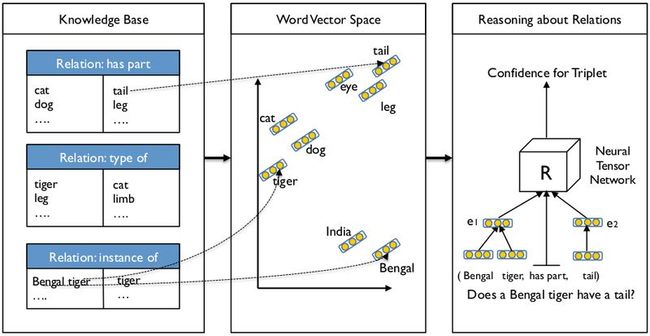
利用这个网络可以进行知识库推理学习。给定训练样本$(e_i,R_k,e_j)$。实体特征已给定，对应输入；关系类型$R$ 对应训练后的网络参数，即网络权重和张量值的集合，每个关系$R$ 对应一个参数集合，样本中含有多个关系。

训练时要构建负例样本，构建的方法为从正例中随机把一个实体替换掉。最终的损失函数为：

$$J(\Omega)=\sum^N_{i=1}\sum^C_{c=1}max(0,1-g(T^{(i)})+g(T_c^{(i)}))+\lambda ||\Omega||^2_2~~~~~~~~~~~~~(2)$$

其中$\Omega$是所有参数的集合${u,W,V,b,E}$。第1，3，4是一般的bp网络的权重参数，最后一个是实体的特征向量，是输入，第二个是张量。$T_c^{(i)}$是第$i$个样本对应的反例。

根据损失函数算出上述参数的偏导数，按一般的梯度下降法或L-BFGS等算法训练网络，训练出来的一个参数集对应一个关系。

文中给出的对应图示为：

一个关系对是一个命题，我们要判定一个命题的置信度。把实体向量（已知）传入具体网络（关系参数已知）输出的结果即为置信度。

 

二、等价变换

我们观察公式$e_1^T\times W \times e_2$，记第一个特征向量$e_1$为$x$，第二个为$y$，皆为列向量（本文中所有向量如未说明，皆为列向量）。该公式改写为：

$$f(x,y;W)=x^T\times W \times y=\sum W\otimes (x\times y^T)~~~~~~~~~~~~~(3)$$

其中$\otimes$圈乘符号，两矩阵对应元素相乘作为新矩阵，$\times$为矩阵叉乘，$\sum$对矩阵的所有元素求和。

此函数可等价表示为：

$$f(x,y;W)=\sum_{i,j} w_{ij}x_i y_j$$

每个矩阵$W$对应一个$slice$，对应函数用$f_i$表示，共$k$个。

此时我们利用一个技巧，把矩阵$W$压扁，拉长成一个向量$s$，$s=(w_{1,1},w_{2,1},...,w_{k,k})^T；$然后把矩阵$x\times y^T$也压扁，拉长成一个向量$z$，$z=(x_1y_1,x_2y_1,...,x_ky_k)^T$。保持原矩阵元素不变，然后二维降成一维。矩阵和拉长后的向量之间可以相互转换，生成网络结构时我们把矩阵拉长成为向量，在训练时计算梯度要把向量还原为矩阵。

砸扁拉长之后，上述公式变为：

$$f(x,y;W)=s^Tz$$

很显然的是，$z$作为两个原始向量的$x$,$y$的二次项$x_iy_j$集合,$s$是二次项系数，函数$f$是关于$x,y$的二次多项式。

每个片(slice)对应一个矩阵记为$W_i$,忽略关系下标$R$;对应一个长向量$s_i$;对应一个函数$f_i$，所有片的向量组成一个矩阵：

$$S=\begin{bmatrix} s_1^T \\ s_2^T \\ ...\\s_k^T\end{bmatrix}$$

这个矩阵$S$我称之为张量矩阵，与张量$W_R^{[1:k]}$等价，此时公式$(1)$中的张量项表示为：

$$e_1^TW_R^{[1:k]}e_2=\begin{bmatrix} f_1 \\ f_2 \\ ...\\f_k\\ \end{bmatrix}=S\times z$$

到此为止，忽略关系下标，我们重写公式$(1)$所表示的网络结构为：

$$g=u^T(\begin{bmatrix} V \\ S \\\end{bmatrix}\times \begin{bmatrix} x \\ y \\ z\\\end{bmatrix}+b)~~~~~~~~~~~~~(4)$$

这就是一个经典的三层bp神经网络了，输入层为$x,y$以及它们的二次向量$z$，第一层权重矩阵为原权重矩阵$V$与张量矩阵$S$的合体。

等价变换之后，我们实现这个模型就变得方便多了！

 

三、引申应用

通过修改该网络的输入内容，损失函数，可以作为推荐系统的模型，特征训练等其它方面的应用。

 

四、思考

该模型的本质是在经典的bp神经网络的输入层中加入了二次项，从而大大的提高了推断的准确率。

如果把学习的数据看成一个物体的话，传统的bp神经网络看到的只是物体的边界，然后根据边界的线性特征进行学习，对物体的内部特征一无所知。也即传统网络是基于一维的数据进行学习，在该模型中，加入了输入数据的二次项，等同于把物体进行2维展开，看过《三体》的应该对其中把原子进行高维展开然后在上面雕刻电路图的宏大场景记忆犹新。物体从1维展开为2维，其信息量应该从$I^1\rightarrow I^2$，信息以维度级别暴增。

如此看来，我们平常的专志于增加样本的特征个数，只是在同维度的范围内增加信息量，并没有改变维度的层次。

以此类推，我们可以在此基础上继续展开到3维（3次项），4维（4次项），。。。，当然，计算量与内存也是需要解决的问题。

或者是，我们不去改变输入信息的维度，你展开，或者不展开，数据都在那里，蕴含的信息都没有变。我们不改变输入，而改变我们的大脑（网络）的学习模式。结构决定性质，目前的神经网络的所有节点都是加和节点，我们或许可以扩展一下，增加一类新的节点，叫乘和节点，这种节点并不是对所有输入进行加权加和，而是加权相乘即$\sum w_ix_i \rightarrow \prod (w_i+x_i)$。直觉上来说，这应该是跟本文中的模型等价的，这两种模型可以相互转换。