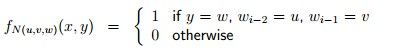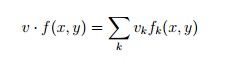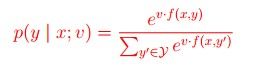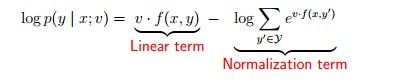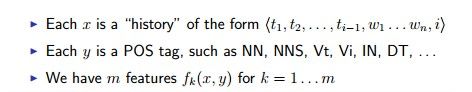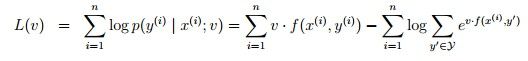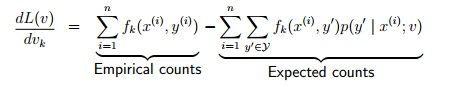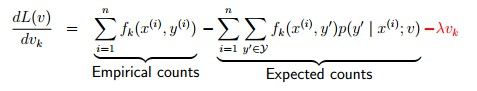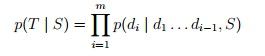最近用使开发的过程中出现了一个小问题，顺便记录一下原因和法方--模型参数
==============================================================
== all is based on the open course nlp on coursera.org week 7,week 8 lecture ==
================================================================
1.The Language Modeling Problem
当初抛开我们之前讲的马尔科夫模型的假设，对于一门言语的义定，定肯不能单简依赖于个每单词的前两个单词，这是知识。比如英语中的动词态形就和主语有关。那么我会怎么斟酌一个言语模型呢，很多是面上这样一个情况：
我们之前讲的Trigram模型也可以用这样的情势来表现：
那么我们要用我们加增的一些义定，一种naive的法方就是选取一些参数来成生模型：
可以象想，这是很难驾御的。但是我们可以用这样的模型来理论上地表现一些例子。
而面上要讲的Log-Liner Model以可就入加这些信息，并使其可作操。
2.Log-linear models
2.1 Define
我们首先用对Language Model的描述来引入log-linear model，Log-linear model际实上是可以引入到很多问题里头的。
这里我先作如下义定：
然后我们义定feature(参数)，一个参数就是一个函数，把x，y映射到一个体具的值
一般来讲，我们设定一个参值数选择为binary的值，要么为1，要么为0
然后假设我们有m个不同的参数，对于一组(x,y)，我们就有一个长度为m的参值数向量：
比如在language model中我们有这样一系列的参数：
在际实中，这些参数的数量是非常多的，为了便方，我们常经常使用便简的方法来表现一些类似的参数：
其中N(u,v,w)把每一组u,v,w映射为一个不同的整数，这一组参数的数量就是不同u,v,w的数量，其实这也就是trigram model的义定，只不过我们用另一种方法表达出来而已。
2.2 Result
这样我们就失掉了一组m个参数，同时我们再义定一个长度为m的向量v，然后我们以可就把(x,y)映射为一个“score”(得分)了：
其实就是数学中的向量的点乘。
2.3 Further Define
我们接下来再进一步用log-linear model来表现我们的Language model：
我们有一个X是input空间，Y是一个无限的词语空间，我们使：
这就是我们的log-linear模型下的言语模型了，意注e的指数其实就是我们面上所说的"score"
为什么叫log linear 模型呢？我们对双方取log看一下：
一览无余了是吧
2.4 for other problem
除了Language Model，log liner的法方还可以用到其他问题上，比如说tagging problem(这个问题的描述在之前的日记有讲：点击打开)
我们要做的是从新计设feature函数，以及转变一下 history的的义定(也就是面上的x)，面上我们是使x=w1,w2…wi-1
在tagging problem中我们使：
这样就是 tagging problem 的log linear模型了，所以说log linear可以应用于比较广的围范。面上我们会细详讲 Tagging Problem中的log-linear model
3.Maximum-Likelihood Estimation for Log-liner Model
3.1 introduction
面上分析下怎么从练训数据中失掉参数，选择的法方叫做ML(大最似然估计)
我们有的就是一系列的x和y
首先选择v:
其中L(v)为：
它叫做似然函数。
有了似然函数，我们以可就选择一种叫做Gradient Ascent的法方，也就是求使L函数大最的v
这个其实就是梯度回升，就是在L上对v求导，失掉梯度，然后一步步用梯度趋近大最值(这其实和梯度下落是相似的，体具可以见这里的分部容内)
然后我们每次迭代使v加上 （β乘以这个导数），β是学习时选择的参数，叫做学习速率。
每日一道理
站在历史的海岸漫溯那一道道历史沟渠：楚大夫沉吟泽畔，九死不悔；魏武帝扬鞭东指，壮心不已；陶渊明悠然南山，饮酒采菊……他们选择了永恒，纵然谄媚诬蔑视听，也不随其流扬其波，这是执著的选择；纵然马革裹尸，魂归狼烟，也要仰天长笑，这是豪壮的选择；纵然一身清苦，终日难饱，也愿怡然自乐，躬耕陇亩，这是高雅的选择。在一番选择中，帝王将相成其盖世伟业，贤士迁客成其千古文章。
3.2 Regularization
如果L只是单简地面上那种情势，法算很可能会过合拟，一些v会成变非常大来更好地增大似然函数，但种这增大是畸形的，叫做overfitting
处理的法方很多，最单简的一种就是入加regularization的分部，也就是：
这样的话如果v过大就会导致penalty
那么：
########面上的课程绝对细讲了log linear model对于Tagging和Parse问题的案方，我选单简的写一个=========
########其实模型都是相似的===============================================================
4、Log-Linear Models for History-based Parsing
4.1回想下Log-Linear Taggers
好吧，这段我懒了，没有写log linera tagger的容内，所以在这充补总结一下，其实也不是很杂复
大概就是这样的一个模型，可以看出其实就是2.4的容内。
4.2 History-Based Models
有了tag后以，我们可能还会有需求去求的一个parse，也就是法语树，一步步来。
假设我们可以将一颗树表现为一系列的decisions，假设为m个，我们有：
意注这里的m一不定是句子的长度，我们可以做很多decision来表现句子树的结构
然后我们义定：
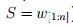表现这个句子
那么对于一棵树的probability就是：
Over------就这么单简，关键是我们要怎么来计设我们的decision
意注和4.1比对一下，我们如果把decision换成tag的容内，就成变了Tagger的问题
4.3Ratnaparkhi's Parser:
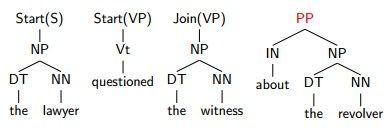
再继承我们的容内之前，先放一个例子在这，好继承描述：
面上重要讲的是一个叫做Ratnaparkhi的人的model，好吧，又是一个90后的model……
他的模型重要分三层：
1. Part-of-speech tags
这分部就是单简的tag的model，个每decision就是一个tag的选择
2. Chunks
Chunks其实就是短语分部的模型：
也就是面上那一排tag，其正式点的义定就是：有所儿子都是
Part-of-speech tags的节点
如何表现它的decision呢？我们用SART和JOIN来表现
一览无余？再加上第一层的模型，当初我们的decision已经有2*n个了：
3. Remaining structure
Remaining structure，我们看一下这颗tree还有什么remaining了呢？更高层的树的结构
我们将用Check来在第二层的础基上来表现这棵树：Check=NO 或者 YES
首先我们跑一次第二层，Check直一置设为NO，不加增什么作操，直到：
我们置设Check=YES，那么生发奇迹的时辰到了，看到没，一组Start和Join消逝了，取而代之的是一个Chunk:PP
我们再继承，CHECK继承为NO：
看到没，在选择Check为YES的时候就把上一个start的分部合并成一个号符！！！
这样继承到最后，我们就失掉了终究的decision：
4.4 Applying a Log-Linear Model
其实比较单简，就是di作为入输，而<d1…di-1,S>作为history
其中A表现有所可能的action(decision)
那么当初还有一个大最的问题，怎么计设我们的 f ？！！
Ratnaparkhi的模型中重要还是关联了decision的分部，我们一样可以对decision停止trigram或者bigram模型的计设，这是和前以的义定一样的，然后将各分部混杂起来就会失掉很多的f了。
4.5 Search Problem
在POS tagging问题中我们可以用使Viterbi algorithm的原因是我们有如下假设：
但是当初的decision可能依托之前的意任一个decision，动态规划是没辙了。。。。
这一分部会在下一周的课程讲到。^_^
文章结束给大家分享下程序员的一些笑话语录： 程序语言综述
CLIPPER 程序员不去真的猎捕大象，他们只是购买大象部分的库然后花几年的时间试图综合它们。
DBASE 程序员只在夜间猎捕大象，因为那时没人会注意到他们还在使用石弓。
FOXPRO 程序员开始使用更新更好的步枪，这使他们花掉比实际狩猎更多的时间学习新的射击技术。
C 程序员拒绝直接购买步枪，宁可带着钢管和一个移动式机器车间到非洲，意欲从零开始造一枝完美的步枪。
PARADOX 程序员去非洲时带着好莱坞关于猎捕大象的电影剧本，他们认为照剧本行事就会逮到一头大象。
ACCESS 程序员在没有任何猎象经验的经验下就出发了，他们穿着华丽的猎装、带着全部装备，用漂亮的望远镜找到了大象，然后发觉忘了带扳机。
RBASE 程序员比大象还要稀少，事实上，如果一头大象看到了一个RBASE程序员，对他是个幸运日。
VISUAL ACCESS 程序员装上子弹、举起步枪、瞄准大象，这使大象感到可笑，究竟谁逃跑。他们无法抓住大象，因为由于他们对多重控制的偏爱，他们的吉普车有太多的方向盘因而无法驾驶。
ADA、APL和FORTRAN 程序员与圣诞老人和仙女一样是虚构的。
COBOL 程序员对和自己一样濒临灭绝的大象寄予了深切的同情。
