LeetCode-Unique Paths

Unique Paths

A robot is located at the top-left corner of a m x n grid (marked 'Start' in the diagram below).

The robot can only move either down or right at any point in time. The robot is trying to reach the bottom-right corner of the grid (marked 'Finish' in the diagram below).

How many possible unique paths are there?

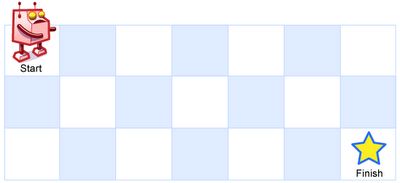
Above is a 3 x 7 grid. How many possible unique paths are there?

Note: m and n will be at most 100.

题意：给定一个m*n的二维方格，从方格的左上角开始走，每次只能向下或者向右走一步直到方格的右下角结束，求总共有多少条不同路径。

解题：从左上角走到右下角，每次只能向下或者向右走一步，不管怎么走都需要m+n-2步才能走到，而这其中有m-1步是向下走，有n-1是向右走，只用从这m+n-2个位置中选择m-1个位置，则剩余的位置表示向右走。容易求得值是C^{m-1_{m+n-2,利用杨辉三角即可。}}

 

Unique Paths II

Now consider if some obstacles are added to the grids. How many unique paths would there be?

An obstacle and empty space is marked as 1 and 0 respectively in the grid.

For example,

There is one obstacle in the middle of a 3x3 grid as illustrated below.

[

  [0,0,0],

  [0,1,0],

  [0,0,0]

]

The total number of unique paths is 2.

Note: m and n will be at most 100.

在问题二中放置了一些障碍物，1表示有障碍物，0表示可以走，求总共有多少条不重复路径。

解题：看到这个题的第一反映是使用广度优先搜索或者深度优先搜索找出所有的路径，尝试之后发现超时，只好另想方法。

因为每次都只能向下和向右行走，因此对每个方格来说只能从它左边和上边的格子进入当前方格，从起点开始到达当前方格的路径数量也就等于从起点开始分别到它左边和上边方格的路径数的总和。

根据上边的思路可以求出从起点到每一个方格的路径个数（如果方格中放置了障碍物则不可通过）

1	1	1
1	0	1
1	1	2

 

 

 

 1   int uniquePathsWithObstacles(vector<vector<int> > &obstacleGrid) {

 2         // Start typing your C/C++ solution below

 3         // DO NOT write int main() function

 4         int m = obstacleGrid.size();

 5         if(m<=0){

 6             return 0;

 7         }

 8         int n = obstacleGrid[0].size();

 9         if(n<=0){

10             return 0;

11         }

12         if(obstacleGrid[0][0]==1){

13             return 0;

14         }

15         

16         int map[101][101];

17         map[0][0]=1;

18         for(int i=1;i<m;i++){

19             if(obstacleGrid[i][0]==1)

20                 map[i][0]=0;

21             else

22                 map[i][0]=map[i-1][0];

23         } 

24         for(int i=1;i<n;i++){

25              if(obstacleGrid[0][i]==1)

26                 map[0][i]=0;

27             else

28                 map[0][i]=map[0][i-1];

29         } 

30         for(int i=1;i<m;i++)

31             for(int j=1;j<n;j++){

32                 if(obstacleGrid[i][j]==1){

33                     map[i][j]=0;

34                 }

35                 else

36                     map[i][j]=map[i-1][j]+map[i][j-1];

37             }

38             

39         return map[m-1][n-1];

40     }