Leetcode | N-Queens I & II

N-Queens I

The n-queens puzzle is the problem of placing n queens on an n×n chessboard such that no two queens attack each other.

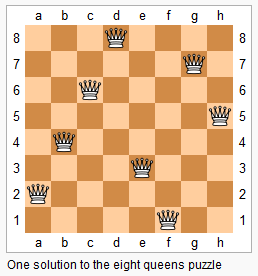
Given an integer n, return all distinct solutions to the n-queens puzzle.

Each solution contains a distinct board configuration of the n-queens' placement, where 'Q' and '.' both indicate a queen and an empty space respectively.

For example,
There exist two distinct solutions to the 4-queens puzzle:

[

 [".Q..",  // Solution 1

  "...Q",

  "Q...",

  "..Q."],



 ["..Q.",  // Solution 2

  "Q...",

  "...Q",

  ".Q.."]

]

Wiki：任两个皇后都不能处于同一条横行、纵行或斜线上。八皇后问题可以推广为更一般的n皇后摆放问题：这时棋盘的大小变为n×n，而皇后个数也变成n。当且仅当 n = 1 或 n ≥ 4 时问题有解。

回溯，用了一个数组col[i]来表示第i列是不是已经放了queen。

对于(row1, col1)和(row2, col2)这两个位置，如果它们在同一对角线上，那么有abs(row1-row2) = abs(col1-col2)。

class Solution {

public:

    vector<vector<string> > solveNQueens(int n) {

        if (n == 2 || n == 3) {

            return ret;

        }

        vector<string> sol(n, string(n, '.'));

        vector<bool> col(n, false);

        bt(n, 0, col, sol);

        return ret;

    }

    

    void bt(int n, int r, vector<bool> &col, vector<string> &sol) {

        if (r >= n) {

            ret.push_back(sol);

            return;

        }

    

        for (int i = 0; i < n; ++i) {

            if (col[i]) continue;



            bool diag = false;

            for (int j = r - 1; j >= 0; --j) {

                for (int m = 0; m < n; ++m) {

                    if (abs(j - r) == abs(m - i) && sol[j][m] == 'Q') {

                        diag = true;

                        break;

                    }

                }

            }   

            

            if (!diag) {

                col[i] = true;

                sol[r][i] = 'Q';

                bt(n, r + 1, col, sol);

                col[i] = false;

                sol[r][i] = '.';

            }

        }

        

    }



private:

    vector<vector<string> >  ret;

};

 N-Queens II

Follow up for N-Queens problem.

Now, instead outputting board configurations, return the total number of distinct solutions.

 

和N-Queens I 类似，同样需要回溯。

前面回溯的时候需要用到一个额外的数组col[i]，而且用到了sol这个数组来判断对角线元素。

网上的解决方案更巧妙些，用到一个数组sol[i]，存的是第i行可解的列号。

当处理到第r行时，检查前r-1行，看sol[0...r-1]有没有等于i的，有就代表了该列已经有queen了。然后再检查对角线上的。

 1 class Solution {

 2 public:

 3     int totalNQueens(int n) {

 4         if (n == 2 || n == 3) {

 5             return 0;

 6         }

 7         vector<int> sol(n, -1);

 8         total = 0;

 9         bt(n, 0, sol);

10         return total;

11     }

12     

13     void bt(int n, int r, vector<int> &sol) {

14         if (r >= n) {

15             total++;

16             return;

17         }

18     

19         for (int i = 0; i < n; ++i) {

20             bool valid = true;

21             for (int j = r - 1; j >= 0; --j) {

22                 for (int m = 0; m < n; ++m) {

23                     if (sol[j] == i || abs(j - r) == abs(sol[j] - i)) {

24                         valid = false;

25                         break;

26                     }

27                 }

28             }   

29             

30             if (valid) {

31                 int t = sol[r];

32                 sol[r] = i;

33                 bt(n, r + 1, sol);

34                 sol[r] = t;

35             }

36         }

37         

38     }

39 

40 private:

41     int total;

42 };

 第三次写，在返回值统计。至此leetcode三遍刷完。

 1 class Solution {

 2 public:

 3     int totalNQueens(int n) {

 4         if (n <= 0) return 0;

 5         vector<int> colSetted(n, -1);

 6         return recurse(n, 0, colSetted);

 7     }

 8     

 9     int recurse(int n, int row, vector<int> &colSetted) {

10         if (row >= n) {

11             return 1;

12         }

13         

14         int count = 0;

15         for (int i = 0; i < n; ++i) {

16             if (colSetted[i] == -1) {

17                 bool couldSet = true;

18                 for (int j = 0; j < n; ++j) {

19                     if (colSetted[j] != -1 && abs(row - colSetted[j]) == abs(i - j)) {

20                         couldSet = false;

21                         break;

22                     }

23                 }

24                 if (couldSet) {

25                     colSetted[i] = row;

26                     count += recurse(n, row + 1, colSetted);

27                     colSetted[i] = -1;

28                 }

29             }

30         }

31         return count;

32     }

33 };