算法起步之Kruskal算法
说完并查集我们接着再来看这个算法,趁热打铁嘛。什么是最小生成树呢,很形象的一个形容就是铺自来水管道,一个村庄有很多的农舍,其实这个村庄我们可以看成一个图,而农舍就是图上的每个节点,节点之间有很多的路径,而铺自来水管道目的就是为了让每家都能用上自来水,而至于自来水怎么铺就不关心了,而铺管子的人就会想如何才能最生材料,那么最省材料的一条路径就是我们这个图的最小生成树。而如何去构建一个最小生成树呢?这个就用到了我们之前说的贪心策略。这里的觉得点就是一直寻找安全边,所以构建最小生成树的过程可以描述成,循环一直寻找安全边加入到树中,直到树中包含所有节点,什么是安全边?安全边的定义就是假设集合A是我们的最小生成树的子集,每一步都是选择一条边是的A还是最小生成树的子集则那条边就是安全边。
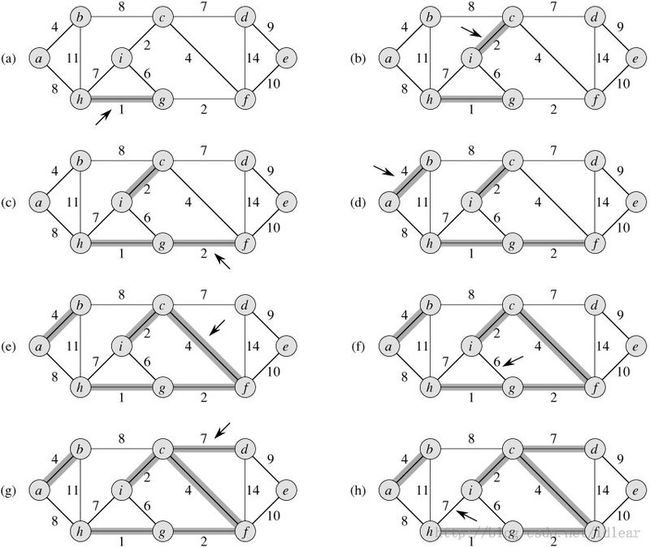
根据安全边选择策略不同有两种最短路径算法,分别是Kruskal算法跟prim算法。我们先来说Kruskal算法。首先我们先看一下图,我觉得图比说要好理解的多。
大家可能已经看出来了,kruskal算法寻找安全边的方式,就是在所有的边中找最小的表,只要两个节点是两个不相交集合,就加入到最小生成树中,直到所有的节点都连接起来。我用汉字写一下伪代码:
1循环所有的边;2构建一个最小优先队列;3构建一个并查集;4直到构建成最小生成树{ 从优先队列取出一个值,判断两个节点是不是不相交集合,是否加入到最小树中。 }结束
下面我们就安装伪代码来写。可能相比之前的代码要多一点,但是基本思想都一样,代码多是因为要写一个javabean跟实现一个并查集,并查集我们在上一篇已经讲过http://blog.csdn.net/idlear/article/details/19556587,最小优先队列也已经说过http://blog.csdn.net/idlear/article/details/18997685大家可以参考之前的文章。
这个是边的javabean不需要解释了吧。
class Bian implements Comparable<Bian>{
private int left;
private int right;
private int value;
public Bian(int i, int j, int k) {
this.left=i;
this.right=j;
this.value=k;
}
public int getLeft() {
return left;
}
public void setLeft(int left) {
this.left = left;
}
public int getRight() {
return right;
}
public void setRight(int right) {
this.right = right;
}
public int getValue() {
return value;
}
public void setValue(int value) {
this.value = value;
}
@Override
public int compareTo(Bian o) {
if (this.getValue()>o.getValue()) {
return -1;
}
return 1;
}
}
并查集。
class Ufs{
private int[] father;
private int[] rank;
public void makeset(int max) {
father = new int[max];
rank = new int[max];
for (int i = 0; i < father.length; i++) {
father[i] = i;
}
}
public void union(int x, int y) {
if (rank[x] > rank[y]) {
father[y] = x;
} else {
if (rank[x] == rank[y]) {
rank[y]++;
}
father[x] = y;
}
}
public int findset(int x) {
if (father[x] != x) {
father[x] = findset(father[x]);
}
return father[x];
}
}
核心代码其实就是一个循环过程,而之前的代码也全是在先前的准备工作。这里如果有几个类没有见过都是java中的工具类,这些类的作用可以查一下api文档。
public void kruskal(int[][] map) {
Ufs ufs=new Ufs();
ufs.makeset(map.length);
ArrayList list=new ArrayList();
for (int i = 0; i < map.length; i++) {
for (int j = 0; j < map.length; j++) {
if(map[i][j]!=0){
Bian b=new Bian(i,j,map[i][j]);
list.add(b);
}
}
}
int max=0;
while(max<=map.length-1){
Collections.sort(list);
Bian b=(Bian) list.remove(1);
int x=b.getLeft();
int y=b.getRight();
if(ufs.findset(x)!=ufs.findset(y)){
ufs.union(x, y);
System.out.println("连接"+x+","+y+"路径长度为"+b.getValue());
max++;
}
}
}
友情提示:转载请注明出处【作者idlear 博客http://blog.csdn.net/idlear/article/details/19301373】