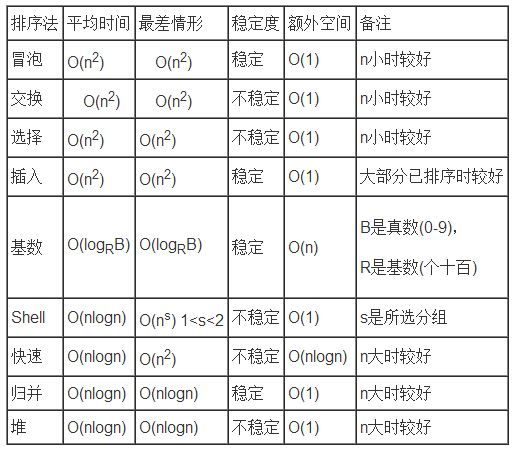
各种排序算法总结
明天就要去参加阿里巴巴的实习生笔试了,虽然没想着能进去,但是态度还是要端正的,也没什么可以准备的,复习复习排序吧。
1 插入排序
void InsertSort(int a[], int n)
{
for (int i=1; i<n; ++i) {
int key = a[i];
int j = i - 1;
while(j>=0 && a[j]>key) {
a[j+1] = a[j];
--j;
}
a[j+1] = key;
}
}
插入排序是稳定的排序,平均和最坏时间复杂度是O(n^2)。最好的时间复杂度是O(n),对应于全部排好序的情况。
2 冒泡排序
void BubbleSort(int a[], int n)
{
for (int i=1; i<n; ++i) {
for(int j=0; j<n-i; ++j) {
if(a[j]>a[j+1]) {
inttemp = a[j];
a[j] = a[j+1];
a[j+1] = temp;
}
}
}
}
冒泡排序是稳定的排序,平均和最坏时间复杂度是O(n^2)。
3 选择排序
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在已排好序的数列的最后,直到全部待排序的数据元素排完。选择排序是不稳定的排序方法。
void SelectSort(int a[], int n)
{
for (int i=0; i<n-1; ++i) {
for(int j=i+1; j<n; ++j) {
if(a[i]>a[j]) {
inttemp = a[i];
a[i] = a[j];
a[j] = temp;
}
}
}
}
选择排序是不稳定的,因为,在一趟选择,如果当前元素比一个元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中2个5的相对前后顺序就被破坏了平均和最坏时间复杂度是O(n^2)。
4 希尔排序(缩小增量排序)
该方法的基本思想是:先将整个待排元素序列分割成若干个子序列(由相隔某个“增量”的元素组成的)分别进行直接插入排序,然后依次缩减增量再进行排序,待整个序列中的元素基本有序(增量足够小)时,再对全体元素进行一次直接插入排序。因为直接插入排序在元素基本有序的情况下(接近最好情况),效率是很高的,因此希尔排序在时间效率上比前两种方法有较大提高。
void ShellSort(int a[], int n)
{
for (int gap=n/2; gap>0; gap/=2) {
for(int i=0; i<gap; ++i) {
for(int j=i+gap; j<n; j+=gap) {
if(a[j]<a[j-gap]) {
int temp = a[j];
int k = j-gap;
while (k>=0&&a[k]>temp) {
a[k+gap] = a[k];
k -= gap;
}
a[k+gap] = temp;
}
}
}
}
}
void ShellSortImproved(int a[], int n)
{
for (int gap=n/2; gap>0; gap/=2) {
for(int j=gap; j<n; ++j) {
if(a[j]<a[j-gap]) {
inttemp = a[j];
intk = j - gap;
while(k>=0 && a[k]>temp) {
a[k+gap] = a[k];
k -= gap;
}
a[k+gap] = temp;
}
}
}
}
希尔排序是不稳定的。由于多次插入排序,我们知道一次插入排序是稳定的,不会改变相同元素的相对顺序,但在不同的插入排序过程中,相同的元素可能在各自的插入排序中移动,最后其稳定性就会被打乱,所以shell排序是不稳定的。使用希尔增量时,最坏运行时间是O(n^2),使用Hibbard增量时,最坏运行时间是O(n^3/2)。
5. 堆排序
void MaxHeapify1(int a[], int n, int i)
{
int l = LEFT(i);
int r = RIGHT(i);
int largest;
if (l<n&& a[l]>a[i])
largest= l;
else
largest= i;
if (r<n&& a[r]>a[largest])
largest= r;
if (largest!=i) {
swap(a[i], a[largest]);
MaxHeapify1(a, n, largest);
} else
return;
}
void MaxHeapify2(int a[], int n, int i)
{
int c, largest;
while (1){
c= LEFT(i);
if (c>=n)
break;
if (a[i]<a[c])
largest= c;
else
largest= i;
if (c+1<n) {
if(a[largest]<a[c+1])
largest= c + 1;
}
if (largest!=i) {
swap(a[i], a[largest]);
i= largest;
} else
break;
}
}
void HeapSort(int a[], int n)
{
for (int i=n/2-1; i>=0;--i)
MaxHeapify1(a, n, i);
for (int i=n-1; i>0; --i) {
swap(a[i], a[0]);
MaxHeapify1(a, i, 0);
}
}
堆排序是原地排序,但是不是稳定排序。时间复杂度O(nlogn)。
6 归并排序
void Merge(int a[], int p, int q, int r)
{
int n1 = q - p + 1;
int n2 = r - (q+1) +1;
int *L = new int[n1+1];
int *R = new int[n2+1];
for (int i=0; i<n1; ++i)
L[i] = a[p+i];
for (int i=0; i<n2; ++i)
R[i] = a[q+1+i];
L[n1] = INT_MAX;//哨兵
R[n2] = INT_MAX;
int i = 0, j = 0;
for (int k=p; k<=r; ++k) {
if (L[i]<=R[j])
a[k] = L[i++];
else
a[k] = R[j++];
}
delete[] L;
delete[] R;
}
void MergeSort(int a[], int p, int r)
{
if (p<r) {;
int q = ((r-p)>>1) + p;
MergeSort(a, p, q);
MergeSort(a, q+1, r);
Merge(a, p, q, r);
}
}
合并过程中我们可以保证如果两个当前元素相等时,我们把处在前面的序列的元素保存在结果序列的前面,这样就保证了稳定性。所以,归并排序也是稳定的排序算法。时间复杂度是O(nlogn)。可以在空间复杂度O(1)的条件下实现归并排序。
7. 快速排序
被快速排序所使用的空间,依照使用的版本而定。使用原地(in-place)分区的快速排序版本,在任何递归调用前,仅会使用固定的额外空间。然而,如果需要产生O(log n)嵌套递归调用,它需要在他们每一个存储一个固定数量的信息。因为最好的情况最多需要O(log n)次的嵌套递归调用,所以它需要O(log n)的空间。最坏情况下需要O(n)次嵌套递归调用,因此需要O(n)的空间。
void Median3(int a[], int p, int r)
{
int median = p + ((r-p)>>1);
if (a[p]>a[median])
swap(a[p], a[median]);
if (a[p]>a[r])
swap(a[p], a[r]);
if (a[median]>a[r])
swap(a[median], a[r]);
swap(a[median], a[r]);
}
int Partition1(int a[], int p, int r)
{
Median3(a, p, r);
int x = a[r];
int i = p - 1;
for (int j=p; j<=r-1; ++j) {
if (a[j]<=x) {
++i;
swap(a[i], a[j]);
}
}
swap(a[i+1], a[r]);
return i+1;
}
int Partition2(int a[], int p, int r)
{
Median3(a, p, r);
int i = p-1, j = r;
int x = a[r];
for (;;) {
while(a[++i]<x);
while(a[--j]>x);
if (i<j)
swap(a[i], a[j]);
else
break;
}
swap(a[i], a[r]);
return i;
}
void QuickSort(int a[], int p, int r) {
if (p<r) {
int q = Partition2(a, p, r);
QuickSort(a, p, q-1);
QuickSort(a, q+1, r);
}
}
快速排序是不稳定的排序,最差时间复杂度是O(n^2),平均时间复杂度是O(nlogn)。
8. 桶排序
void BucketSort(int a[], int n)
{
int *count = new int[1000];
memset(count, 0, sizeof(int)*1000);
for (int i=0; i<n; ++i) {
++count[a[i]];
}
int k = 0;
for (int i=0; i<1000; ++i){
while(count[i]--){
a[k++] = i;
}
}
}
如果count有M个单元,算法用时O(M+N),桶排序是稳定的排序。但是需要额外的空间。
稳定的排序有:冒泡,插入,归并,基数,桶。