计算机是如何做加法的?(7)——回顾与总结
在前面,运用自顶向下的方式,我们明白了计算机做加法的方式。
继电器的网络
我们最终得到了半加器的模型如下:
而其中的异或器内部又是如下的结构:
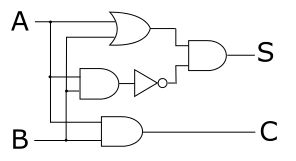
如果只用与门,或门以及非门三种电路来表示,则半加器是这样的:
它由三个与门,一个或门再加一个非门组成。
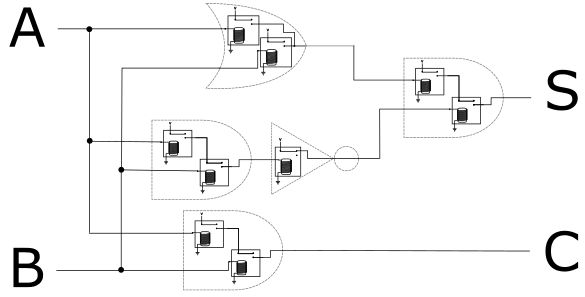
如果把其中的继电器也画出来:
显然,这是一个继电器构成的网络。清点一下,我们发现有9个继电器。
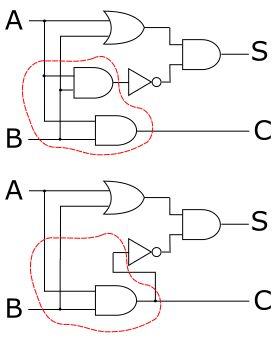
但实际上,注意左下角的两个与门是有点重复的,可以用一个与门来取代。
所以综合来看,只需用7个继电器就可以达到目的了。
当我们分开分析时,可以简化分析的过程,但也可能引入一些不必要的重复,这些需要在综合的时候进行取舍。
另一方面,由于有良好的接口抽象,内部实现细节的调整不会冲击到整体的设计。
当然,对于现代的IC芯片,这里的继电器要换成晶体管。(这同样属于内部实现细节的问题)
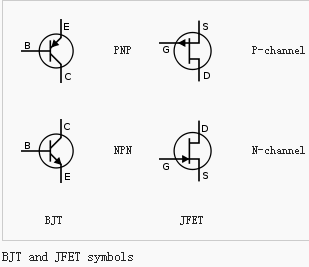
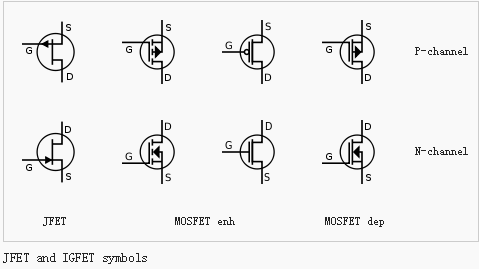
晶体管的符号如下(来自wiki,下同):
又或者是更加先进的场效应管(场效应晶体管):
当然了,功能逻辑还是一样的,都是用输入去控制输出,继电器用的是电磁感应,晶体管则用了半导体的特性。
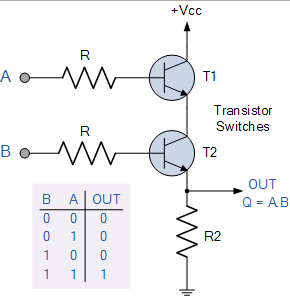
一个与门的示例(来自http://www.electronics-tutorials.ws/logic/log43.gif?81223b):
半导体的通断特性无法像继电器开关那般直观地展示,简单地讲,AB上无电压时,T1,T2就像是绝缘体;有电压时则变成导体。
如果你对它的原理感兴趣,可自行搜索了解更多。
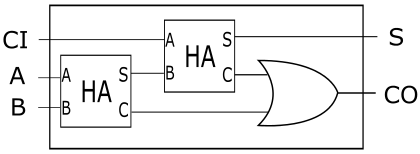
而前面又说到,一个全加器由两个半加器和一个或门构成:
那么,它需要7×2+2=16个继电器。
那么,比如一个四位的加法器就需要16×4=64个继电器开关。
从这里大家也可以感受一下一个简单全加器它里面基本功能元件的数量的一个大概规模。
注:我们倾向于认为与门,或门和非门这些为基础的门电路,又认为比如“与非门”是这些门电路的组合,但实际上有可能对某些晶体管的实现而言,与非门可能是更基础的构件。
人如何做一位数的加法?
在前面,我们曾经留下一个问题:人是如何做两个一位数的加法呢?
记忆之网
你靠的是记忆!
是的,事实就是这样。你其实没有在算,当你看到7+8时,你的脑海里就浮现出了15这个数字。
如果这不能让你信服,不妨看看乘法的情况。
比如问你7×8等于多少,你脱口而出56,你怎么能算得这么快呢?这相当于要做7次或者8次加法,你一定背过乘法口诀!
如果再问你12×13等于多少?傻眼了吧,你还能脱口而出吗?出不来了吧?这是为什么呢?
可是,我们好像没有背过加法口诀?
但其实你要是看看小学一年级的学生的数学作业本,老师会让他们反复的练习一位数的加法,直到形成条件反射!
虽然我们没有主动去背过什么加法表,但反复的练习让我们在不知不觉中已经记住了所有的规则!
太初有道
那么,我们什么时候才是不靠记忆来做加法的呢?
在最初,我们先学会数数,1,2,3,4,5,6,7,8,9,10.反复念叨直至滚瓜烂熟,以此建立数的先后次序,也即所谓大小的概念。
然后,我们怎么做加法呢?
以上截图来自腾讯动漫《龙珠》http://ac.qq.com/ComicView/chapter/id/505436/cid/121
没错,我们靠数指头来做加法!十个指头就是我们的终极武器。这很可能是你小时做2+3时的情形:
你看到一个2,于是你数“1,2”,你边数边伸指头,看到3,你继续数“1,2,3”;
然后你再次从一开始清点所有伸出的指头,1,2,3,4,5,你边清点边把指头缩回去,最终你得出了5是这次加法的结果。
当然,做得多了之后,你就无需再数了,因为你已经记住了。把一位加法弄得滚瓜烂熟之后,多数人甚至都可以轻松地心算两位数加法了:
在算数这个问题上,库林(图中头上零根毛的那位)完全是碾压饺子(头上一根毛的)的节奏。好卑鄙的库林!:)
一种猜测
经过反复的演算,可以这么猜测,我们其实也是在我们脑海中构建了一个一位数加法的网络:
当我们看到比如一个加式:“2+3=”时,这些符号经眼睛传入我们大脑之后引发了相应神经元的一系列电化学反应,最终我们得出了“5”这个结果。
2+3=5,这是一个我们熟知的事实,与其说我们在“运算”,不如说我们只是在记忆之网中把这个结果提取出来。
究竟做了什么?
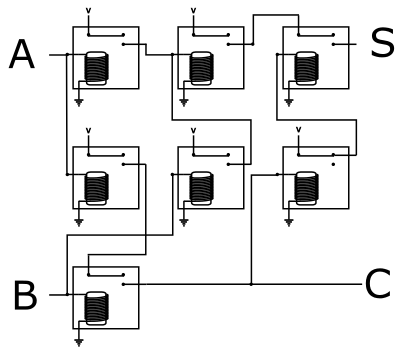
下图是前述7个继电器构成的半加器网络的一个等价连接:
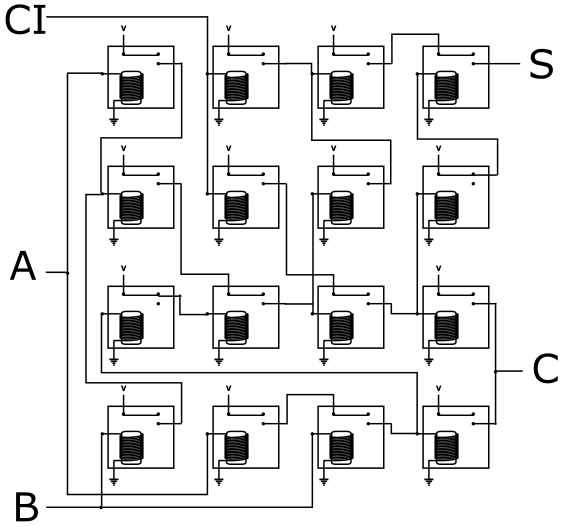
如果以上还不让你觉得复杂,那么再看下如下全加器的一个等价连接,这次有16个继电器开关:
在这里,半加器及门电路级的抽象层全部被丢弃了。如果一开始就给你一堆这样的连接,你能意识到它们是在做二进制的加法吗?
与此类似,在软件层面,如果代码缺少抽象层级,把过多的细节无情地暴露出来,通常也会导致代码难以理解。
对每个继电器(晶体管)而言,它们显然不知道自己在做什么,每个继电器只不过是简单根据输入的情况输出一个响应而已。
一切不过是机械地通通断断而已,所谓“做加法”,只不过我们精心按着加法的逻辑凑出来的一个结果。
显然,你换种方式去连接它们,只要你能凑出加法的逻辑,你都可以说你实现了一个加法器。
当然我们肯定希望用最简单经济的方式去实现它。
网络从哪里来?
那么对于我们人来说呢?我们不妨问自己一个问题:当我们在做加法的时候,我们究竟在做什么?
数字及运算符号经眼睛进入大脑(输入),引发了神经元的一系列充放电反应,最终出来一个结果(输出),看上去与上述过程也很像。
我们脑海中为何会有这样一个对抽象符号作出反应的网络呢?
当我们长到六七岁时,幸福的童年突然就结束了,我们觉得被送到了一所“监狱”(大人们称之为“小学”)一样的地方,学习那些来自阿拉伯的符号,以及一种称为“加法”的运算。用的还是十进制!
自然,这些抽象的有那么一点点反人类的东西让不少小盆友叫苦不迭。
于是乎,经过老师们(或许还有家长们)的威逼利诱(你也可称之为“努力“),这些叫“加法”的东西终于扎根小朋友的脑海。
事实上,如果我们愿意承认的话,我们接受这些知识完全是被动的。
而老师头脑中的网络则可能是来自老师的老师,然后又来自老师的老师的老师...
进化生物学家道金斯在他的《自私的基因》一书中把这种现象与基因的遗传与变异作了对比, 他用了一个词“模因(meme)”来描述这种文化遗传因子,模因在人脑中“繁殖”与“变异”,同时也以其它形式存在如书本,电脑上等。(未来也许不再需要人脑这种介质?)
所谓的”智能“
关于算术的知识能在人脑中不断传承下来,并得到发展,也许是因为我们一度认为这样的东西是人这种聪明的,有智能的生物才能去掌握的。
阿猫阿狗们好像就不能做到这些,或者说做得不好,以至于如果真能做到很简单的一些算术也会当成一条新闻。
但现在,连一堆电路也能做到这些,甚至做得比人类还快还好;另一方面,当我们深入分析做加法的过程时,到了最底层,我们甚至有些疑惑:加法的意义究竟在何处?我们只看到一堆的连线和一些通通断断的器件,意义似乎消解了,只剩下一些“机械的(mechanic)”东西,这或许正是我们能用机器(machine)去做它们的原因。
这一过程真的体现了所谓的“智能”吗?
我们人类或许只是更复杂“机器”而已?又或者说,所谓的”智能“究竟是什么呢?
量变到质变?
据估计,人脑中可能有高达一千亿左右的神经元细胞,然后彼此间以非常复杂的方式连接在一起。
而现在那些超大规模的集成电路,比如cpu的核心,指甲那么大小一片上可以集成高达20亿个晶体管,彼此间的连接同样也是非常复杂,而这一切还在不断的发展中,那么我们会面临怎样的可能性呢?
如果你愿意仔细去思考的话,这些或许是一个很深奥的问题。
以上为大导演史蒂文·斯皮尔伯格(Steven Spielberg)的电影《人工智能》(Artificial Intelligence)的海报。