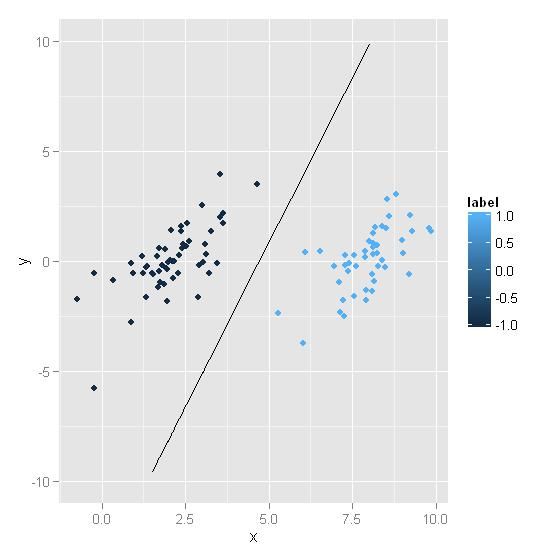
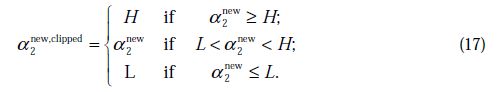SVM支持向量机（四）R语言实现、SMO算法

一、求解支持向量机。

    上篇笔记讲到，如何求解拉格朗日乘子向量。基本的想法就是，每次选出两个乘子，对其他的乘子赋值，此时，只剩两个乘子。问题变成了一个两元一次方程和求二元函数最小值的问题。如果乘子可以更新（既违反了KKT条件），则把其中一个乘子用令一个乘子代替，带入到二元函数中，再求函数取最小值时（通过公式可以看出这是一个开口向上的抛物线），未知数的值。重复上面的过程直到所有的乘子都稳定下来，不再发生变化。此时问题求解成功。

    记要更新的乘子为ai,aj，aj的更新过程如下

其中E1，E2是我们分类的预测值和实际值的差，既wx+b - y 。

K为核函数。 aj每次更新时等于更新前的值加上y2(E1-E2)/n ，这个公式实际上就是上面说的，对开口向上的抛物线求导，令导数等于0求得的解。不过这个公式不太好推导，下面参考的博客里有详细的推导过程。这种写法同时体现了坐标下降的思路，和梯度下降有点像，但梯度下降每次向梯度方向下降固定的步长，而坐标下降一次性达到局部最优的位置。但是，a2new只是抛物线顶点，还不是真正的解。因为还有限制条件，将限制条件画到图上，就是一个正方形，而ai,aj的关系是一条直线，直线截距可正可负，所以要分情况看。如果根据抛物线导数求解的a2new没有落在平行线上和正方形内时，应取直线与正方形的边界值。根据aj,ai的符号是否相同，限制条件的边界值也有所不同：
ai,aj异号
ai,aj同号

    根据上面的公式，每次可以更新一个乘子，由于两个乘子是线性关系，所以另外一个乘子往相反的方向更新即可。由于更新乘子的过程中，使用到了b，所以每次更新完，还得把b也更新一下。b的更新公式为

    当某个乘子a满足 0 < a < C 时，这个乘子所对应的样本就是支持向量，因此有wx+b=1或者wx+b=-1, 因为w可以由乘子计算出来，后面的正负一就是样本的分类，所以，b可以求出来，推导之后b的计算方式也可以写成上面的更新公式。如果两个乘子都不满足0 < a < C ,也就是说两个样本点都不是支持向量，此时，b不能精确到底是多少，但可以肯定在b1和b2之间，这里一般写成两者平均数。

    上面的公式展示了每一次是如何更新一对乘子，并更新b的。
    在简单求解的过程中，可以随机选取一些乘子来更新。如果随机选取到的乘子都不需要再更新，既所有的乘子都满足KKT条件，当这样的情况发生到一定次数时，停止迭代，求解完成。

   下面我们用R语言实现上面算法，测试数据集为《机器学习实战》第6章的简单算法测试数据。原始数据集图：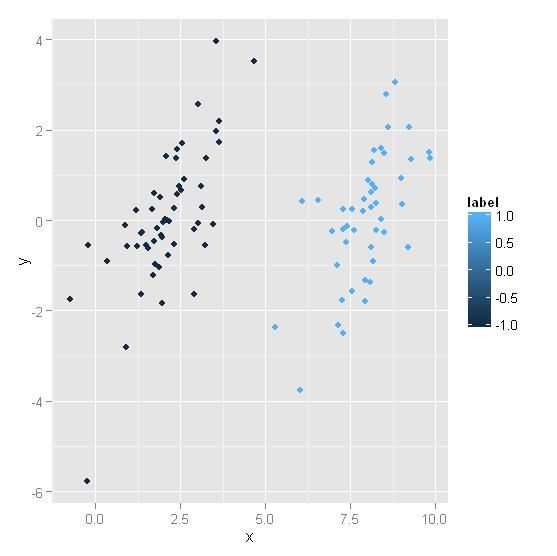

使用如下代码，运行后，画出分隔平面

src <- read.table("D:\\baiduyundownload\\ml\\machinelearninginaction\\Ch06\\testSet.txt",header=F)
names(src) <- c("x","y","label")
#作原始数据图像
library(ggplot2)
qplot(x,y,data=src,geom="point",xlab="x",ylab="y",color=label,position="jitter")
#挑选一个随机数，当选择ai后，随机选取一个aj
selectRandom <- function(i,maxNum){
  j <- i
  while(j == i){
    j <- runif(1,1,maxNum)
  }
  return(j)
}
#选择下一个拉格朗日乘子，如果顶点在限制条件外，应取边界点
nextAlpha <- function(aj,H,L){
  #cat("aj,H,L is ",aj,H,L,"\n")
  if(aj > H){
    aj <- H
  }
  if(aj < L){
    aj <- L
  }
  return(aj)
}
#定义一个核函数，为方便，先实现内积
kernel <- function(vector1,vector2,type="linear"){
  if(type == "linear"){
    return(sum(vector1*vector2))
  }
}
#创建核矩阵，避免重复计算
createKernelMatrix <- function(dataSet){
  n <- nrow(dataSet)
  km <- matrix(rep(0,n*n),nrow=n)
  for(i in 1:n){
    for(j in i:n){
      value <- kernel(dataSet[i,],dataSet[j,])
      km[i,j] <- value
      km[j,i] <- value
    }
  }
  return(km)
}

#简单支持向量机算法
simpleSVM <- function(data,C=0.6,maxIte=40,miss=0.001){
  #初始化数据
  dataSet <- data[,c(1,2)] #数据矩阵，每一行是一个样本
  label <- data$label  #所属分类，1和-1
  aSet <- rep(0,length(label))  #所有乘子初始化为0
  b <- 0
  kernelMatrix <- createKernelMatrix(dataSet)
  #开始迭代
  iter <- 0 
  while( iter < maxIte){
    changedCount <- 0
    for(i in 1:length(label)){
      j <- selectRandom(i,length(label))
      x1 <- dataSet[i,]
      x2 <- dataSet[j,]
      E1 <- sum(aSet*label*kernelMatrix[,i])+b - label[i]
      #是否可以优化？ 违反了KKT条件的都可以优化
      if(((E1*label[i] < -miss) && (aSet[i] < C)) || ((E1*label[i] > miss) && (aSet[i] > 0))){
        E2 <- sum(aSet*label*kernelMatrix[,j])+b - label[j]
        H <- 0
        L <- 0
        if(label[i]*label[j] > 0){
          L <- max(0,aSet[j]+aSet[i]-C)
          H <- min(C,aSet[j]+aSet[i])
        }else{
          L <- max(0,aSet[j]-aSet[i])
          H <- min(C,C+aSet[j]-aSet[i])
        }
        if(L==H){
          cat("L=H continue \n")
          next
        }
        nita <- 2*kernelMatrix[i,j] - kernelMatrix[j,j] - kernelMatrix[i,i]
        if(nita == 0){
          cat("nita is 0 \n")
          next
        }
        newAj <- aSet[j] - label[j]*(E1-E2)/nita
        oldAj <- aSet[j]
      aSet[j] <- nextAlpha(newAj,H,L)
        oldAi <- aSet[i]
        aSet[i] <- aSet[i] + label[i]*label[j]*(oldAj-aSet[j])
        #开始更新b
        if(aSet[i] > 0 && aSet[i] < C){
          b <- b -E1 -label[i]*(aSet[i]-oldAi)*kernelMatrix[i,i] - 
               label[j]*(aSet[j]-oldAj)*kernelMatrix[i,j]
        }else{
           if(aSet[j] > 0 && aSet[j] < C){
             b <- b -E2 -label[i]*(aSet[i]-oldAi)*kernelMatrix[i,j] - 
               label[j]*(aSet[j]-oldAj)*kernelMatrix[j,j]
           }else{
             b1 <- b -E1 -label[i]*(aSet[i]-oldAi)*kernelMatrix[i,i] - 
               label[j]*(aSet[j]-oldAj)*kernelMatrix[i,j]
             b2 <- b -E2 -label[i]*(aSet[i]-oldAi)*kernelMatrix[i,j] - 
               label[j]*(aSet[j]-oldAj)*kernelMatrix[j,j]
             b <- (b1+b2)/2
           }
        }
        changedCount <- changedCount+1
      }   
    }
    if(changedCount == 0){
      iter <- iter+1 #此次没有更新，则iter增加1，直到退出迭代
    }else{
      iter <- 0
    }
  }
  temp <- aSet*label
  w1 <- temp*dataSet[,1]
  w2 <- temp*dataSet[,2]
  w <- c(sum(w1),sum(w2))
  return(list("w"=w,"b"=b,"a"=aSet))
}

model <- simpleSVM(src)
src$calY <- (-model$b - model$w[1]*src$x)/model$w[2] #计算出画线的数据
p <- ggplot(src) + geom_point(aes(x=x,y=y,color=label),position="jitter") #画点
p <- p + geom_line(aes(x=x,y=calY))+ylim(-10,10) #画线
p

感觉还行，不过代码里很多地方写死了，只能用于2维数据，为了不写的太复杂，自己都搞不清，就这样了。

二、SMO算法

  在上面的实现中，我们顺序选取ai然后随机选取aj。这个过程浪费了非常多计算量。从经验来看，绝大多数的样本点都不是支持向量，当优化到该样本时，乘子会变成0。而乘子变成0或C之后基本不会再发生变化，反而那些优化后仍然处于0和C之间的乘子，往往需要不断的优化。SMO算法遵循“启发式”选择方法，既优先优化那些可以一次性优化到位的乘子。然后再优化其他的乘子。SMO通过两层循环来挑选要优化的乘子。

   SMO称选择第一个变量的过程为外层循环。外层训练在训练样本中选取违法KKT条件最严重的样本点。并将其对应的变量作为第一个变量。 该检验是在ε范围内进行的。在检验过程中，外层循环首先遍历所有满足条件0<αj<C的样本点，即在间隔边界上的支持向量点，检验他们是否满足KKT条件，然后选择违反KKT条件最严重的αi。如果这些样本点都满足KKT条件，那么遍历整个训练集，检验他们是否满足KKT条件，然后选择违反KKT条件最严重的αi。
   优先选择遍历非边界数据样本，因为非边界数据样本更有可能需要调整，边界数据样本常常不能得到进一步调整而留在边界上。由于大部分数据样本都很明显不可能是支持向量，因此对应的α乘子一旦取得零值就无需再调整。遍历非边界数据样本并选出他们当中违反KKT 条件为止。当某一次遍历发现没有非边界数据样本得到调整时，遍历所有数据样本，以检验是否整个集合都满足KKT条件。如果整个集合的检验中又有数据样本被 进一步进化，则有必要再遍历非边界数据样本。这样，不停地在遍历所有数据样本和遍历非边界数据样本之间切换，直到整个样本集合都满足KKT条件为止。以上 用KKT条件对数据样本所做的检验都以达到一定精度ε就可以停止为条件。如果要求十分精确的输出算法，则往往不能很快收敛。
   对整个数据集的遍历扫描相当容易，而实现对非边界αi的扫描时，首先需要将所有非边界样本的αi值（也就是满足0<αi<C）保存到新的一个列表中，然后再对其进行遍历。同时，该步骤跳过那些已知的不会改变的αi值。
   在选择第一个αi后，算法会通过一个内循环来选择第二个αj值。因为第二个乘子的迭代步长大致正比于|Ei-Ej|，所以我们需要选择能够最大化|Ei-Ej|的第二个乘子（选择最大化迭代步长的第二个乘子）。在这里，为了节省计算时间，我们建立一个全局的缓存用于保存所有样本的误差值，而不用每次选择的时候就重新计算。我们从中选择使得步长最大或者|Ei-Ej|最大的αj。

    后期实现。

参考文章支持向量机（五）SMO算法 - JerryLead - 博客园

机器学习算法与Python实践之（四）支持向量机（SVM）实现 - zouxy09的专栏 - 博客频道 - CSDN.NET