贝塞尔曲线解析-Cocos2dx 01
在数学的数值分析领域中，贝塞尔曲线（英语：Bézier curve）是电脑图形学中相当重要的参数曲线。更高维度的广泛化贝塞尔曲线就称作贝塞尔曲面，其中贝塞尔三角是一种特殊的实例。
贝塞尔曲线于1962年，由法国工程师皮埃尔·贝塞尔（Pierre Bézier）所广泛发表，他运用贝塞尔曲线来为汽车的主体进行设计。贝塞尔曲线最初由Paul de Casteljau于1959年运用de Casteljau算法开发，以稳定数值的方法求出贝塞尔曲线。
线性贝塞尔曲线[编辑]
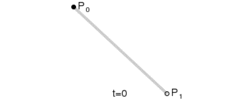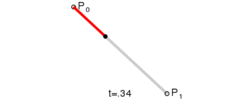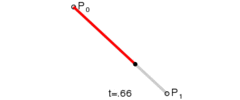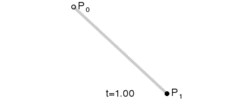
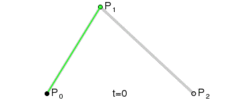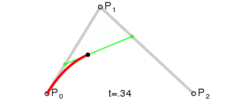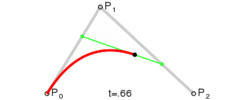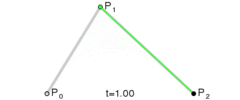
给定点P0、P1，线性贝塞尔曲线只是一条两点之间的直线。这条线由下式给出：
且其等同于线性插值。
线性贝塞尔曲线函数中的t会经过由P0至P1的B（t）所描述的曲线。例如当t=0.25时，B（t）即一条由点P0至P1路径的四分之一处。就像由0至1的连续t，B（t）描述一条由P0至P1的直线。
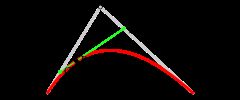
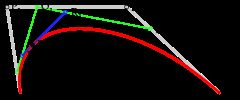
二次方贝塞尔曲线[编辑]
二次方贝塞尔曲线的路径由给定点P0、P1、P2的函数B（t）追踪：
。
TrueType字型就运用了以贝塞尔样条组成的二次贝塞尔曲线。
为建构二次贝塞尔曲线，可以中介点Q0和Q1作为由0至1的t：
由P0至P1的连续点Q0，描述一条线性贝塞尔曲线。
由P1至P2的连续点Q1，描述一条线性贝塞尔曲线。
由Q0至Q1的连续点B（t），描述一条二次贝塞尔曲线。
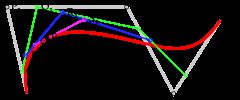
三次方贝塞尔曲线[编辑]
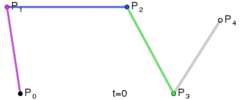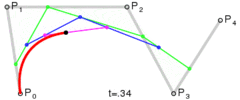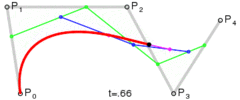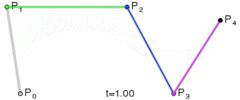
P0、P1、P2、P3四个点在平面或在三维空间中定义了三次方贝塞尔曲线。曲线起始于P0走向P1，并从P2的方向来到P3。一般不会经过P1或P2；这两个点只是在那里提供方向资讯。P0和P1之间的间距，决定了曲线在转而趋进P3之前，走向P2方向的“长度有多长”。
曲线的参数形式为：
。
现代的成象系统，如PostScript、Asymptote和Metafont，运用了以贝塞尔样条组成的三次贝塞尔曲线，用来描绘曲线轮廓。
对于四次曲线，可由线性贝塞尔曲线描述的中介点Q0、Q1、Q2、Q3，由二次贝塞尔曲线描述的点R0、R1、R2，和由三次贝塞尔曲线描述的点S0、S1所建构：
程式范例
曲线的计算可在曲线阵列上将相连点画上直线——点越多，曲线越平滑。
在部分架构中，下以程式码也可由动态规划进行最优化。举例来说，dt是一个常数，cx * t则等同于每次反复就修改一次常数。经反复应用这种最优化后，循环可被重写为没有任何乘法（虽然这个过程不是稳定数值的）。
/*
产生贝塞尔曲线的算法
*/
typedef struct{
float x;
float y;}Point2D;
/*
cp 在此是四个元素的数组:
cp[0] 为起点，或上图中的 P0
cp[1] 为第一控制点，或上图中的 P1
cp[2] 为第二控制点，或上图中的 P2
cp[3] 为结束点，或上图中的 P3
t 为参数值，0 <= t <= 1
*/
Point2D PointOnCubicBezier( Point2D* cp, float t ){
float ax, bx, cx;
float ay, by, cy;
float tSquared, tCubed;
Point2D result;
/*计算多项式系数 */
cx = 3.0 * (cp[1].x - cp[0].x);
bx = 3.0 * (cp[2].x - cp[1].x) - cx;
ax = cp[3].x - cp[0].x - cx - bx;
cy = 3.0 * (cp[1].y - cp[0].y);
by = 3.0 * (cp[2].y - cp[1].y) - cy;
ay = cp[3].y - cp[0].y - cy - by;
/*计算t位置的点值*/
tSquared = t * t;
tCubed = tSquared * t;
result.x = (ax * tCubed) + (bx * tSquared) + (cx * t) + cp[0].x;
result.y = (ay * tCubed) + (by * tSquared) + (cy * t) + cp[0].y;
return result;}
/* ComputeBezier 以控制点 cp 所产生的曲线点，填入 Point2D 结构数组。
调用方必须分配足够的空间以供输出，<sizeof(Point2D) numberOfPoints>>
*/
void ComputeBezier( Point2D* cp, int numberOfPoints, Point2D* curve ){
float dt;
int i;
dt = 1.0 / ( numberOfPoints - 1 );
for( i = 0; i < numberOfPoints; i++)
curve[i] = PointOnCubicBezier( cp, i*dt );}
在历史上，研究贝塞尔曲线的人最初是按照已知曲线参数方程来确定四个点的思路设计出这种矢量曲线绘制法。
如果已知一条曲线的参数方程，系数都已知，并且两个方程里都含有一个参数t，它的值介于0、1之间，表现形式如下所示：
x(t) = ax * t ^ 3 + bx * t ^ 2 + cx * t + x0
y(t) = ay * t ^ 3 + by * t ^ 2 + cy * t + y0
由于这条曲线的起点(x0,y0)是已知的，我们可以用以下的公式来求得剩余三个点的坐标：
x1 = x0 + cx / 3
x2 = x1 + ( cx + bx ) / 3
x3 = x0 + cx + bx + ax
y1 = y0 + cy / 3
y2 = y1 + ( cy + by ) / 3
y3 = y0 + cy + by + ay
仔细观察一下就知道了，无论方程的已知和所求是什么，总是有六个未知数，并且我们总能找到六个等式（记住(x0,y0)总是已知的），也就是说，上面的方法是完全可逆的，因此我们可以根据四个已知点坐标来反求曲线参数公式的系数。稍微一变换就得到了下面这组公式：
cx = 3 * ( x1 - x0 )
bx = 3 * ( x2 - x1 ) - cx
ax = x3 - x0 - cx - bx
cy = 3 * ( y1 - y0 )
by = 3 * ( y2 - y1 ) - cy
ay = y3 - y0 - cy - by
所以说，对于坐标任意的四个已知点，你总能创建一条贝塞尔曲线，这样在逻辑判断及使用中就可以创建自己所需的贝塞尔曲线效果。
参考：
http://zh.wikipedia.org/wiki/貝茲曲線
http://blog.chinaunix.net/uid-20622737-id-3161025.html