【人工智能】贝叶斯网络之结构、参数学习

1、上一篇百度文库的代码

（http://my.oschina.net/SnifferApache/blog/343756#OSC_h1_11）

N = 5;  
dag = zeros(N,N);    
B = 1; E = 2; A = 3; R=4;W = 5; 
dag(B,A) = 1;    
dag(E,[A R]) = 1; 
dag(A,W) = 1; 
discrete_nodes = 1:N;  
node_sizes = 2*ones(1,N);    
  
bnet =mk_bnet(dag,node_sizes,'names',... 
{'bandits','earthquake','broadcast','bells','telephone'},... 
'discrete',discrete_nodes); 
  
bnet.CPD{B} = tabular_CPD(bnet,B,[0.9 0.1]);
bnet.CPD{E} = tabular_CPD(bnet,E,[0.99 0.01]); 
bnet.CPD{W} = tabular_CPD(bnet,W,[0.99 0.35 0.01 0.65]); 
bnet.CPD{R} = tabular_CPD(bnet,R,[0.999 0.01 0.001 0.99]); 
bnet.CPD{A} = tabular_CPD(bnet,A,[0.99 0.1 0.1 0.01 0.01 0.9 0.9 0.99]); 
  
figure  
draw_graph(dag)      

 
%计算铃声响，家中有贼的概率 %按如下方式计算p=P(B=2|A=2): 
engine = jtree_inf_engine(bnet); 
evidence = cell(1,N);  evidence{A} = 2; 
[engine, loglik] = enter_evidence(engine, evidence); 
marg = marginal_nodes(engine, B);
p11 = marg.T(2);

%添加华生致电福尔摩斯的这一条信息，也就是计算p=P(B=2|A=2,w=2): 
evidence{W} = 2; 
[engine, loglik] = enter_evidence(engine, evidence);  
marg = marginal_nodes(engine, B);  
p12 = marg.T(2) 
%得出p12=0.8412 ，与p11相同

%计算铃声响，家里地震的概率 %按如下方式计算p=P(E=2|A=2): 
engine = jtree_inf_engine(bnet);  
evidence = cell(1,N); 
evidence{A} = 2; 
[engine, loglik] = enter_evidence(engine, evidence); 
marg = marginal_nodes(engine, E);
p21 = marg.T(2); 

%添加广播的这一条信息，也就是计算p=P(E=2|A=2,R=2):
evidence{R} = 2; 
[engine, loglik] = enter_evidence(engine, evidence);  
marg = marginal_nodes(engine, E);  
p22 = marg.T(2); 

%添加华生致电福尔摩斯的这一条信息，也就是计算p=P(E=2|A=2,R=2,W=2):
evidence{W} = 2; 
[engine, loglik] = enter_evidence(engine, evidence);  
marg = marginal_nodes(engine, E);  
p23 = marg.T(2)
%得出p23=0.9892

2、BNT参数、结构学习

Bayesian 网络学习指的是通过分析数据儿获得Bayesian网的过程，它包括以下两种情况

①参数学习：已知网络结构，确定网络参数。

②结构学习：既要确定网络结构，又要确定网络参数。

我们可以一个贝叶斯网络看作一个黑箱，那参数学习，结构学习就是创造一个白箱{可能是我造的名词}尽可能模拟这个黑箱！

在前面的基础之上，我们可以轻松画出贝叶斯网络bnet{！当然，其每个节点的CPT都是题目给出的}。经过bnet处理之后的样本数据会输出得到训练数据data

在①情况下，构建一个和bnet节点个数，箭头指向相同的bnet1,接着借助BNT中的工具，将data和bnet1作为参数，就可以学习得到新的贝叶斯网络bnet2；

在②情况下，借助BNT中的工具，将data和其他数据{！具体参数见代码}作为参数，便可学习得到新的贝叶斯网络bnet3。

接下来使用如下语句便可以方便的输出一个贝叶斯网络中各个节点的CPT{！第一节输出CPT的方法容易理解但有些繁琐}

%输出bnet的CPT

CPT = cell(1,N);

for i=1:N

  s=struct(bnet.CPD{i});

  CPT{i}=s.CPT;

end

dispcpt(CPT{1})

dispcpt(CPT{2})

dispcpt(CPT{3})

dispcpt(CPT{4})

dispcpt(CPT{5})

详见代码

%这里使用的例子依然是“福尔摩斯模型”。
%首先我先如上面实验那样建立好贝叶斯网bnet，并手动构造条件概率表CPT。
%然后使用BNT里的函数sample_bnet(bnet)来产生nsamples个数据样本，
%nsamples分别取值20，200，2000。
%然后，再重新建立一个不知道条件概率表的贝叶斯网bnet2（结构和bnet相同），
%并把得到的样本作为训练集代入learn_params()函数进行学习，
%把学习到的条件概率表CPT2与手动构造的CPT进行了比较。参数学习部分代码:

clc;
clear;
%1、构造样本数据data
nsamples = 2000;
samples = cell(N, nsamples);
for i = 1:nsamples
    samples(:,i) = sample_bnet(bnet);
end
data = cell2num(samples);


%2、手动构造和bnet结构相同的bnet1
bnet1 = mk_bnet(dag,node_sizes,'discrete',discrete_nodes);
seed = 0;
rand('state',seed);
bnet1.CPD{B} = tabular_CPD(bnet2,B);
bnet1.CPD{E} = tabular_CPD(bnet2,E);
bnet1.CPD{W} = tabular_CPD(bnet2,W);
bnet1.CPD{R} = tabular_CPD(bnet2,R);
bnet1.CPD{A} = tabular_CPD(bnet2,A);
%参数学习得到新的贝叶斯网络bnet2
bnet2 = learn_params(bnet1,data);

%3、结构学习
order=[1 2 3 4 5];
ns=[2 2 2 2 2];
max_fan_in=2;
%结构学习函数
dag2 = learn_struct_K2(data ,ns, order,'max_fan_in', max_fan_in);
figure
draw_graph(dag2);
bnet3=mk_bnet(dag2,ns,'discrete',order);

利用输出语句CPT的语句可以得到

原贝叶斯网络bnet的CPT

1 : 0.9000 

2 : 0.1000 

1 : 0.9900 

2 : 0.0100 

1 1 : 0.9900 0.0100 

2 1 : 0.1000 0.9000 

1 2 : 0.1000 0.9000 

2 2 : 0.0100 0.9900 

1 : 0.9990 0.0010 

2 : 0.0100 0.9900 

1 : 0.9900 0.0100 

2 : 0.3500 0.6500 

新贝叶斯网络bnet2的CPT

1 : 0.9030 

2 : 0.0970 

1 : 0.9890 

2 : 0.0110 

1 1 : 0.9888 0.0112 

2 1 : 0.0990 0.9010 

1 2 : 0.1500 0.8500 

2 2 : 0.0000 1.0000 

1 : 0.9995 0.0005 

2 : 0.0000 1.0000 

1 : 0.9877 0.0123 

2 : 0.3302 0.6698 

和（http://my.oschina.net/SnifferApache/blog/343756#OSC_h2_7）所示的条件概率表相比，相差无几

新贝叶斯网络bnet3的CPT

Reference to non-existent field 'CPT'.

shit，只能用第一节中的旧方法了……

engine2 = jtree_inf_engine(bnet3);
%新证据
evidence2 = cell(1,N);
[engine2, loglike] = enter_evidence(engine2, evidence2);

%计算节点B的CPT
marg2 = marginal_nodes(engine2,B);
marg2.T   
%计算节点E的CPT
marg2 = marginal_nodes(engine2,E);
marg2.T 
%计算节点W的CPT
marg2 = marginal_nodes(engine2,[W A]);
marg2.T 
%计算节点R的CPT
marg2 = marginal_nodes(engine2,[R E]);
marg2.T 
%计算节点A的CPT
marg2 = marginal_nodes(engine2,[A B E]);
marg2.T

输出如下

Error using jtree_inf_engine/enter_evidence (line 55)

must define CPD 1

事实证明结构学习得到的bnet3不包含CPT字段，导致无法计算CPT，此处挖坑待高人解答吧。

{！补充：

BNT中参数学习函数：

•最大似然性估计learn_params( ) ;

•贝叶斯方法bayes_update_params( ) 。

结构学习函数：

•K2 算法learn_struct_K2( ) ；

•贪婪搜索GS(Greedy Search) 算法learn_struct_gs( )；

•爬山HC ( Hill Climbing) 算法learn_struct_hc( ) 。

BNT提供的多种推理引擎：

•联合树推理引擎jtree_inf_engine();

•全局联合树推理引擎global_joint_inf_engine();

•.信念传播推理引擎belprop_inf_engine();

•变量消元推理引擎var_elim_inf_engine()

}

3、两道人工智能练习题

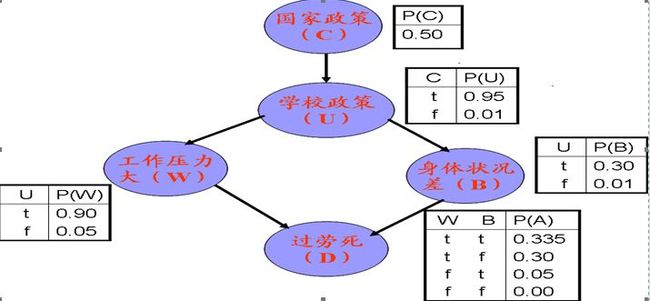
3.1、试采用matlab的贝叶斯工具箱BNT完成以下“过劳死”问题的建模。要求代码中使用BNT工具箱中的贝叶斯结构、参数学习命令。给出网络学习代码及运行结果。

仅供参考

clear;
clc
N=5;
%构造网络结构
dag=zeros(N,N);
C=1;U=2;W=3;B=4;D=5;
dag(C,U)=1;
dag(U,[W,B])=1;
dag([W,B],D)=1;
discrete_nodes=1:N;
node_sizes=2*ones(1,N);
bnet=mk_bnet(dag,node_sizes,'names',{'country','university','workhard','badbody','die'},'discrete',discrete_nodes);
%构造概率表
bnet.CPD{C}= tabular_CPD(bnet,C,[0.5,0.5]);
bnet.CPD{U}= tabular_CPD(bnet,U,[0.99,0.05,0.01,0.95]);
bnet.CPD{W}= tabular_CPD(bnet,W,[0.95,0.10,0.05,0.90]);
bnet.CPD{B}= tabular_CPD(bnet,B,[0.99,0.70,0.01,0.30]);
bnet.CPD{D}= tabular_CPD(bnet,D,[1.00,0.95,0.70,0.665,0.00,0.05,0.30,0.335]);
figure 
draw_graph(dag);

%输出bnet的CPT
CPT = cell(1,N);
for i=1:N
  s=struct(bnet.CPD{i});
  CPT{i}=s.CPT;
end
dispcpt(CPT{1})
dispcpt(CPT{2})
dispcpt(CPT{3})
dispcpt(CPT{4})
dispcpt(CPT{5})
%输出结束

engine=jtree_inf_engine(bnet);
evidence=cell(1,N);
engine=enter_evidence(engine,evidence);
%计算节点C的CPT
marg=marginal_nodes(engine,C);
marg.T
%计算节点D的CPT
evidence{W}=2;
evidence{B}=2;
[engine,loglik]=enter_evidence(engine,evidence);
marg1=marginal_nodes(engine,[W B D]);
marg1.T(2)

%构造样本数据
nsamples=2000;
samples=cell(N,nsamples);
for i=1:nsamples
    samples(:,i)=sample_bnet(bnet);
end
data=cell2num(samples);
bnet1=mk_bnet(dag,node_sizes,'discrete',discrete_nodes);
%手动构造条件概率表CPT
seed=0;
rand('state',seed);
bnet1.CPD{C}=tabular_CPD(bnet1,C);
bnet1.CPD{U}=tabular_CPD(bnet1,U);
bnet1.CPD{W}=tabular_CPD(bnet1,W);
bnet1.CPD{B}=tabular_CPD(bnet1,B);
bnet1.CPD{D}=tabular_CPD(bnet1,D);
%进行参数学习
bnet2=learn_params(bnet1,data);
%验证学习结果
engine2=jtree_inf_engine(bnet2);
evidence2=cell(1,N);
engine2=enter_evidence(engine2,evidence2);
%计算节点C的CPT
marg=marginal_nodes(engine2,C);
marg.T
%计算节点D的CPT
evidence2{W}=2;
evidence2{B}=2;
[engine2,ll]=enter_evidence(engine2,evidence2);
m=marginal_nodes(engine2,[W B D]);
m.T(2) 

%结构学习
order=[1 2 3 4 5];
ns=[2 2 2 2 2];
max_fan_in=2;
%结构学习函数
dag2 = learn_struct_K2(data ,ns, order,'max_fan_in', max_fan_in);
figure
draw_graph(dag2);
bnet3=mk_bnet(dag2,ns,'discrete',order);

3.2、试采用核函数方法对下列数据进行非线性分类。给出matlab具体代码，及采用训练样本进行测试得到的准确率结果。      

        x=[0 1 0 1 2 -1];

        y=[0 0 1 1 2 -1];

        z=[-1 1 1 -1 1 1;

       其中，（x,y）代表二维的数据点，z 表示相应点的类型属性。

仅供参考

clc;
clear;
%手工录入+1类和-1类的数据
sp = [1,0; 0,1; 2,2; -1,-1] %positive
sn = [0,0; 1,1;]%negative
data = [sp;sn]
datalabel=[1 1 1 1 0 0]; %分类
%groups为logical类型
groups = ismember(datalabel,1);
%交叉标记data为train和test两部分
[train,test]=crossvalind('holdOut',groups);
%核函数 mlp，预测准确率为0.3
svmStruct=svmtrain(data(train,:),groups(train),'kernel_function','mlp','showplot',true);
%预测准确率为0
%svmStruct2=svmtrain(data,groups,'kernel_function','mlp','showplot',true);
%加入参数[0.5 -0.5]之后，预测准确率为0.6
svmStruct3 = svmtrain(data,groups,'kernel_function','mlp','mlp_params',[0.5 -0.5],'showplot',true);
 
title(sprintf('核函数'))
cp=classperf(groups);%用来评价分类器
classes = svmclassify(svmStruct3,data(test,:),'showplot',true);
classperf(cp,classes,test);
cp.CorrectRate

4、参考资料

[1] 贝叶斯网络-使用MATLAB工具集，http://www.cnblogs.com/xjx-user/archive/2013/04/14/3020273.html