棋盘问题
在一个 2^k * 2^k 个方格组成的棋盘中,若恰有一个方格与其它方格不同,则称该方格为一特殊方格,称该棋盘为一特殊棋盘。显然特殊方格在棋盘上出现的位置有 4^k 种情形。因而对任何 k>=0 ,有 4^k 种不同的特殊棋盘。下图所示的特殊棋盘为 k=2 时 16 个特殊棋盘中的一个。
在棋盘覆盖问题中,要用下图中 4 中不同形态的 L 型骨牌覆盖一个给定的特殊棋牌上除特殊方格以外的所有方格,且任何 2 个 L 型骨牌不得重叠覆盖。易知,在任何一个 2^k * 2^k 的棋盘中,用到的 L 型骨牌个数恰为 (4^k-1)/3 。
用分治策略,可以设计解棋盘问题的一个简捷的算法。
当 k>0 时,将 2^k * 2^k 棋盘分割为 4 个 2^(k-1) * 2^(k-1) 子棋盘,如下图所示。
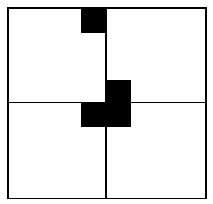
特殊方格必位于 4 个较小子棋盘之一中,其余 3 个子棋盘中无特殊方格。为了将这 3 个无特殊方格的子棋盘转化为特殊棋盘,我们可以用一个 L 型骨牌覆盖这 3 个较小的棋盘的汇合处,如下图所示,这 3 个子棋盘上被 L 型骨牌覆盖的方格就成为该棋盘上的特殊方格,从而将原问题化为 4 个较小规模的棋盘覆盖问题。递归的使用 这种分割,直至棋盘简化为 1x1 棋盘。
#include<stdio.h> #include<stdlib.h> int title=1;// L型骨牌的编号 int chess[1000][1000];
/*递归方式实现棋盘覆盖算法
nowr----------现在的行位置
nowc----------现在的列位置
sx------------特殊方块的行位置
sy------------特殊方块的列位置
size----------当前棋盘的规模
*/
void chessquestion(int nowr,int nowc,int sx,int sy,int size)
{
if(size==1) return ;
int t=title++;
int s=size/2;//从棋盘最中间的位置开始查找。
//特殊位置在现在位置的左上角。
if(sx<nowr+s&&sy<nowc+s)
{
chessquestion(nowr,nowc,sx,sy,s);
}
else//否则视右下角为特殊位置
{
chess[s-1+nowr][s-1+nowc]=t;
chessquestion(nowr,nowc,s-1+nowr,s-1+nowc,s);
}
//特殊位置出现在右上角
if(sx<nowr+s&&sy>=nowc+s)
{
chessquestion(nowr,nowc+s,sx,sy,s);
}
else//不在则视左下角为特殊位置
{
chess[nowr+s-1][nowc+s]=t;
chessquestion(nowr,nowc+s,nowr+s-1,nowc+s,s);
}
//特殊位置在现在位置的左下角。
if(sx>=nowr+s&&sy<nowc+s)
{
chessquestion(nowr+s,nowc,sx,sy,s);
}
else//否则视右上角为特殊位置
{
chess[s+nowr][s-1+nowc]=t;
chessquestion(nowr+s,nowc,s+nowr,s-1+nowc,s);
}
//特殊位置出现在右下角
if(sx>=nowr+s&&sy>=nowc+s)
{
chessquestion(nowr+s,nowc+s,sx,sy,s);
}
else//不在则视左下角为特殊位置
{
chess[nowr+s][nowc+s]=t;
chessquestion(nowr+s,nowc+s,nowr+s,nowc+s,s);
}
}
int main()
{
int k,sx,sy;
int i,j;
printf("请输入2^k的值(大小必须是2的幂数)\n");
scanf("%d",&k);
printf("请输入特殊坐标x的值\n");
scanf("%d",&sx);
printf("请输入特殊坐标x的值\n");
scanf("%d",&sy);
chessquestion(0,0,sx,sy,k);
for(i=0;i<k;i++)
{
for(j=0;j<k;j++)
{
printf("%d\t",chess[i][j]);
}
printf("\n");
}
system("pause");
return 0;
}