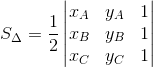初学算法 - 求凸包的Garham's Scan算法的C++实现

    所谓凸包，就是一个计算几何（图形学）中的概念。用不严谨的话来讲，给定二维平面上的点集，凸包就是将最外层的点连接起来构成的凸多边型，它能包含点集中所有的点。维基百科对集合X的凸包（Convex Hull）有四个定义，分别为：

• The (unique) minimal convex set containing X            ---  包含集合X的最小凸集合

• The intersection of all convex sets containing X          --- 所有包含集合X的凸集合的交集

• The set of all convex combinations of points in X.       --- 集合X中所有点的凸组合的集合

• The union of all simplices with vertices in X.                --- 集合X中所有单一顶点的集合

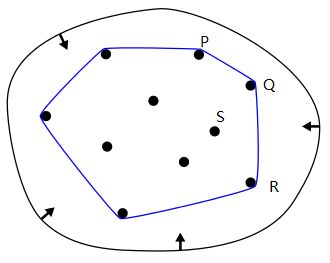
    对于二维凸包，不如我们把平面上的一些点想象为“钉子”，而你正将一个橡皮筋撑的足够大，以至于所有“钉子”都在你的橡皮筋包围的区域里。现在我们松开它。“啪”的一声，橡皮筋会尽可能的收缩到极致，而这时撑起橡皮筋的这些“钉子”构成的集合， 也就是凸包。

                                            

    

    通过观察，我们可以知道“最左”和“最右”的两个点一定在构成凸包的集合里。而Garham's Scan算法也正是注意到了这点。另外，如果我们按照顺时针方向观察凸包，如P->Q->R，在每一个点上凸包都是“右拐”的（当然，也可能构成一条直线）。

                                        

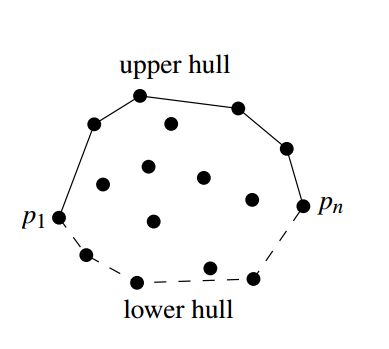
    使用两个链表Lupper和Llower分别表示凸包的上半部分（Upper Hull）和下半部分（Lower Hull），Garham的算法可以通过如下伪代码描述：

Algorithm CONVEXHULL(P)
Input. A set P of points in the plane.
Output. A list containing the vertices of CH(P) in clockwise order.
 Sort the points by x-coordinate, resulting in a sequence p1,..., pn.
 Put the points p1 and p2 in a list Lupper, with p1 as the first point.
 for i ← 3 to n
     do Append pi to Lupper.
         while Lupper contains more than two points and the last three points in Lupper do not make a right turn
             do Delete the middle of the last three points from Lupper.
 Put the points pn and pn−1 in a list Llower 6 , with pn as the first point.
 for i ← n−2 downto 1
     do Append pi to Llower.
         while Llower contains more than 2 points and the last three points in Llower do not make a right turn
             do Delete the middle of the last three points from Llower.
 Remove the first and the last point from Llower to avoid duplication of the points where the upper and lower hull meet.
 Append Llower to Lupper, and call the resulting list L.
 return L

    

    现在问题转到了已知三点A,B,C的坐标，如何确定C点是否在向量AB的左边了。

    对于这个问题，我们可以使用几何学的一个结论：有向面积。三角形的有向面积可以通过一个行列式求得：

            (不知道这个行列式怎么计算的童鞋可以去补补线代了~)

    如果C在AB方向的左边，那么这个行列式求得的值是正的，反之为负。在设计程序时，我们只需要知道这个行列式值的正负，而并不关心它具体的值，因此就不需要再做一个除法了。

/**
 * Calculate the doubled directed area of pqs
 */
long long Area2( Point p, Point q, Point s)
{
    return p.x*q.y - p.y*q.x
          +q.x*s.y - q.y*s.x
          +s.x*p.y - p.x*s.y;
}

//Determinate whether s is on the left side of a directed line p->q
bool ToLeft( Point p, Point q, Point s)
{
    return Area2(p,q,s)>0;
}

    整个算法可以写成如下的代码：

/**
 Created on 2015-10-12 11:24:04

 Description : Generate the Convex Hull via the Graham's Scan Algorithm
               Time Cost : O(nlogn)
               Thanks to Tsinghua Univ. MOOC Computational Geometry 2015
               As the answer of CG2015 PA1-1 Convex Hull
               (http://dsa.cs.tsinghua.edu.cn/oj/course.shtml?courseid=39)

 Author: ChenZheng / Arc001
 Email : [email protected]
 Copyright 2015 Xi'an University of Posts & Telecommunications
*/

#include <iostream>
#include <cstdio>
#include <algorithm>
#include <list>

using namespace std;

enum Point_Status {isExtreme, notExtreme};

struct Point{
    long long x,y;
    int index;
    Point_Status status;

    bool operator < (const Point & rhs) const
    {
        if(x == rhs.x)
        {
            return y < rhs.y;
        }
        return x < rhs.x;
    }
};

long long Area2( Point p, Point q, Point s); //这里不再重复
bool ToLeft( Point p, Point q, Point s);

Point S[100005];
list<Point> upper_hull, lower_hull;

int main()
{
    int n;
    long long ans = 1;
    scanf("%d",&n);
    for(int i=1;i<=n;i++){
        scanf("%lld%lld",&S[i].x,&S[i].y);
        S[i].index = i;
        S[i].status = notExtreme;
    }

    sort(&S[1],&S[n+1]);

    upper_hull.push_back(S[1]);
    upper_hull.push_back(S[2]);

    list<Point>::iterator it,it2,it3;
    for(int i=3; i<=n; i++)
    {
        upper_hull.push_back(S[i]);
        it = it2 = it3 = upper_hull.end();
        --it; --it; --it;
        --it2; --it2;
        --it3;
        //cout<<it3->index<<" pushed!"<<endl;

        while(upper_hull.size()>2 && ToLeft(*it,*it2,*it3))
        {
            upper_hull.erase(it2);
            //cout<<it2->index<<" deleted! "<<it3->index<<" "<<Area2(*it,*it2,*it3)<<endl;
            it = it2 = it3 = upper_hull.end();
            --it; --it; --it;
            --it2; --it2;
            --it3;
        }
        //cout<<upper_hull.size()<<endl<<endl;
    }
    upper_hull.pop_back();

    lower_hull.push_back(S[n]);
    lower_hull.push_back(S[n-1]);

    for(int i=n-2; i>=1; i--)
    {
        lower_hull.push_back(S[i]);

        it = it2 = it3 = lower_hull.end();
        --it; --it; --it;
        --it2; --it2;
        --it3;
        while(lower_hull.size()>2 && ToLeft(*(it),*(it2),*(it3)))
        {
            lower_hull.erase(it2);
            it = it2 = it3 = lower_hull.end();
            --it; --it; --it;
            --it2; --it2;
            --it3;
        }
    }
    lower_hull.pop_back();

    //cout<<lower_hull.size()<<endl;
    int count_vertex = 0;
    for(it = upper_hull.begin(); it != upper_hull.end(); it++)
    {
        S[it->index].status = isExtreme;
        //cout<<it->index<<endl;
        count_vertex++;
    }

    for(it = lower_hull.begin(); it != lower_hull.end(); it++)
    {
        S[it->index].status = isExtreme;
        //cout<<it->index<<endl;
        count_vertex++;
    }

    for(int i=1; i<=n; i++){        //这里在计算这道题的答案，与算法关系不大
        if(S[i].status == isExtreme)
        {
            ans *= i;
            ans %= (n+1);
            //cout<<i<<endl;
        }
    }

    ans *= count_vertex;
    ans %= (n+1);

    printf("%lld\n",ans);
    return 0;
}