SAGE入门:开源数学系统之集大成者
自己博客上写的入门,原文地址:http://cvnote.info/SAGE入门:开源数学系统之集大成者
最近在学习Sage这款开源数学软件系统,百度了一下发现国内关注的还比较少,所以写一个Sage的介绍吧。
Sage(http://www.sagemath.org)是一款类似于Maple、Matlab、Mathematica之类的数学软件,GPL许可,项目的目标是:
Mission: Creating a viable free open source alternative to Magma, Maple, Mathematica and Matlab.
Sage可以干什么?介绍中有这么一句:“这款开源软件的支持者称Sage能够完成从12维物体到计算全球变暖效应数学模型中的降雨量的任何事情。”Sage包含了从线性代数、微积分,到密码学、数值计算、组合数学、群论、图论、数论等各种初高等数学的计算功能。
Sage的一大特点是整合了众多优秀的开源数学软件,使用户可以在Sage中方便的使用这些库中的相应功能。Sage目前整合了近一百个开源的数学库,这其中包括著名的ATLAS、BLAS、LAPACK、Boost、GSL、SciPy等等,完整列表可以查看这里。
Sage基于并使用Python,Python程序可以在Sage中直接运行,也可以在Sage中使用Python的各种库,感觉就像是提供了一个包含各种数学功能的Python环境。
使用Sage,你可以:
- 下载安装Sage到本地(下载链接)
- 使用在线版本。Sage目前提供两种在线平台,分别是早期的The Sage Notebook和最近推出的SageMathCloud
下面是Sage的一些功能。
Sage Notebook
地址:http://www.sagenb.org/
也可以在本地Sage命令行下使用 notebook() 开启,相当于Maple的工作簿Worksheet,虽然看着有点简陋,但功能还是很强大的,可以输入Sage 命令,渲公式、显示图形等。
SageMathCloud
地址:https://cloud.sagemath.com/
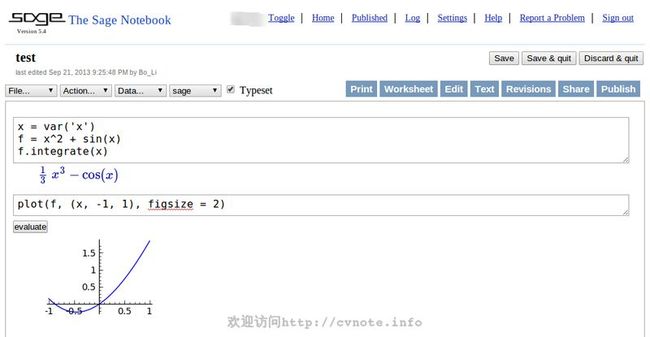
SageMathCloud类似于一个在线的写作编程平台,注册后可以在里面建立工程,编辑各种源文件。这里建立了一个test工程,然后新建了一个.sagews(Sage Worksheet)工作簿文件,界面和Maple的worksheet很像,可以在里面输入代码,点击运行键可以显示结果。
虽然目前还是beta版但是感觉还是挺好用的。除了Worksheet还可以新建terminal,效果和本地的Linux terminal一样,输入 sage 可以进入Sage命令行,用法和Python命令行很像,可以使用 help() 和tutorial()产看帮助与教程。
基本计算
和大多数数学软件系统一样,很简单易用。比如求2013的质因子:
|
1
2
3
4
|
sage
:
x
=
2013
sage
:
f
=
factor
(
x
)
sage
:
f
3
*
11
*
61
|
或者矩阵求逆
|
1
2
3
|
sage
:
matrix
(
[
[
1
,
2
]
,
[
3
,
4
]
]
)
^
(
-
1
)
[
-
2
1
]
[
3
/
2
-
1
/
2
]
|
符号计算
Sage的符号计算非常好用,可以用 x = var('var_name') 声明符号变量。例如求一个函数的积分
|
1
2
3
4
5
|
sage
:
a
=
var
(
'a'
)
sage
:
x
=
var
(
'x'
)
sage
:
f
=
a *
sin
(
x
)
+
1
/
x
sage
:
f
.
integrate
(
x
)
-
a*
cos
(
x
)
+
log
(
x
)
|
或者解个方程
|
1
2
|
sage
:
solve
(
x
^
2
+
a
,
x
)
[
x
==
-
sqrt
(
-
a
)
,
x
==
sqrt
(
-
a
)
]
|
绘图功能
比如画出上面 f = a * sin(x) + 1 / x 在a=1时,在x=1~10的图像。 figsize 为图像大小
|
1
2
|
sage
:
f
=
f
.
substitute
(
a
==
1
)
sage
:
plot
(
f
,
(
x
,
1
,
10
)
,
figsize
=
2
)
|
可以得到
除了2D,Sage还支持3D绘图,具体可以查看文档。
基本的数域与环
Sage支持在整数环( ZZ)、有理数域( QQ)、实数域( RR)、复数域( CC),以及更高级的多项式环、有限域(Finite Field)等集合上进行计算。这里要顺便复习一下抽象代数,比如一些简单的概念:
|
1
2
3
4
5
6
7
8
|
sage
:
QQ
.
gens
(
)
# 有理数域的单位元和零元素
(
1
,
)
sage
:
QQ
.
zero
(
)
0
sage
:
CC
.
gens
(
)
# 复数域的单位元和零元素
(
1.00000000000000
*
I
,
)
sage
:
CC
.
zero
(
)
0.000000000000000
|
运算的范围不同,结果也不同。例如:
|
1
2
3
4
5
6
|
sage
:
ratpoly
.
<
t
>
=
PolynomialRing
(
QQ
)
# 定义ratpoly为基于有理数域上t的多项式环
sage
:
realpoly
.
<
z
>
=
PolynomialRing
(
RR
)
# 定义realpoly为基于实施域上z的多项式环
sage
:
factor
(
t
^
2
-
2
)
t
^
2
-
2
sage
:
factor
(
z
^
2
-
2
)
(
z
-
1.41421356237310
)
*
(
z
+
1.41421356237310
)
|
外部软件/库接口
对于集成的外部开源数学软件库,Sage提供的方便的接口进行调用。在Sage中使用这些接口可以方便的将不同语言、不同功能的数学软件库整合在同一程序中,这也使得Sage集成了众多开源数学软件之所长。当然这些外部数学库很多都非常专业,实际应用中应该只会用到其中很有限的一部分。这里举两个官网Sage Tutorial里的例子。
用GP/PARI求(本)原根(Primitive root)
GP/PARI是一个做数论的包(wiki)。原根是什么呢,上过数论但是忘了的请面壁:(
抄一下wiki吧还是
在
时,定义
对模
的指数
为使
成立的最小的正整数
。由前知
一定小于等于
,若
,则称
是模
的原根。
对正整数
,如果 a 是模 m 的原根,那么 a 是整数模n乘法群(即加法群 Z/mZ 的可逆元,也就是所有与 m 互素的正整数构成的等价类构成的乘法群)Zn×的一个生成元。
生成元是一个很数论中很重要的概念,在一个整数模n乘法群中,生成元可以通过不断与自己相乘(然后再模n),生成群中的所有元素。元根可以用PARI中的 znprimroot(n) 函数来求。
|
1
2
|
sage
:
gp
(
'znprimroot(7)'
)
Mod
(
3
,
7
)
|
或
|
1
2
|
sage
:
pari
(
'znprimroot(7)'
)
Mod
(
3
,
7
)
|
得到3是模7乘法群的一个元根。
用Maxima在有理域求矩阵特征向量
Maxima用LISP编写的计算机代数系统 (Computer Algebra System),前身是Macsyma,Matlab和Mathematica等软件的出现都受到在Macsyma的影响。在Sage中可以方便调用Maxima代数系统。例如下面在求特征向量并转换到有理域向量空间的例子,代码同样来自官网Sage Tutorial,加了一些注释:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
sage
:
A
=
maxima
(
"matrix ([1, 0, 0], [1, -1, 0], [1, 3, -2])"
)
# 生成矩阵
sage
:
eigA
=
A
.
eigenvectors
(
)
# 计算特征响亮
sage
:
V
=
VectorSpace
(
QQ
,
3
)
# V是一个有理数域上的3维向量空间,
sage
:
eigA
# 输出格式为[[[特征值],[特征值重数]],[[特征向量0],[特征向量1],[特征向量2]]]
[
[
[
-
2
,
-
1
,
1
]
,
[
1
,
1
,
1
]
]
,
[
[
[
0
,
0
,
1
]
]
,
[
[
0
,
1
,
3
]
]
,
[
[
1
,
1
/
2
,
5
/
6
]
]
]
]
sage
:
v1
=
V
(
sage_eval
(
repr
(
eigA
[
1
]
[
0
]
[
0
]
)
)
)
;
lambda1
=
eigA
[
0
]
[
0
]
[
0
]
sage
:
v2
=
V
(
sage_eval
(
repr
(
eigA
[
1
]
[
1
]
[
0
]
)
)
)
;
lambda2
=
eigA
[
0
]
[
0
]
[
1
]
sage
:
v3
=
V
(
sage_eval
(
repr
(
eigA
[
1
]
[
2
]
[
0
]
)
)
)
;
lambda3
=
eigA
[
0
]
[
0
]
[
2
]
sage
:
M
=
MatrixSpace
(
QQ
,
3
,
3
)
# M是一个有利数域上的3×3维的矩阵空间
sage
:
AA
=
M
(
[
[
1
,
0
,
0
]
,
[
1
,
-
1
,
0
]
,
[
1
,
3
,
-
2
]
]
)
sage
:
b1
=
v1
.
base_ring
(
)
# b1 == QQ 是有理数域
sage
:
AA*
v1
==
b1
(
lambda1
)
*
v1
# 验证特征值定义A*v = lambda1*v
True
sage
:
b2
=
v2
.
base_ring
(
)
sage
:
AA*
v2
==
b2
(
lambda2
)
*
v2
True
sage
:
b3
=
v3
.
base_ring
(
)
sage
:
AA*
v3
==
b3
(
lambda3
)
*
v3
True
|
注意到 M() 、 V() 、 b1() 、 b2() 、 b3() 都相当于类型转换,限定运算在有理数域上进行。另外这里的特征向量没有单位化,因为是在有理数域上。
与Latex协同
Sage内部可以与Latex协同。对于任意Sage对象foo,可以通过调用 latex(foo) 得到其Latex输出。例如:
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
|
sage
:
var
(
'z'
)
z
sage
:
latex
(
z
^
12
)
z
^
{
12
}
sage
:
latex
(
integrate
(
z
^
4
,
z
)
)
\
frac
{
1
}
{
5
}
\
,
z
^
{
5
}
sage
:
latex
(
'a string'
)
\
verb
|
a
|
\
phantom
{
\
verb
!
x
!
}
\
verb
|
string
|
sage
:
latex
(
QQ
)
\
Bold
{
Q
}
sage
:
latex
(
matrix
(
QQ
,
2
,
3
,
[
[
2
,
4
,
6
]
,
[
-
1
,
-
1
,
-
1
]
]
)
)
\
left
(
\
begin
{
array
}
{
rrr
}
2
&
4
&
6
\
\
-
1
&
-
1
&
-
1
\
end
{
array
}
\
right
)
|
类似地,本地Sage命令行中使用 view(foo) 则会
SageTex Package
通过 \usepackage{sagetex} 在tex文件中使用SageTex Package,可以直接在tex文件中插入Sage命令,并随Latex输出结果到pdf。具体可参见官方Sage Tutorial。
小结
刚刚发现Sage的时候觉得很好很强大啊,本身基于Python,可以使用Python的库,也会比较好上手。同时又提供了比较方便的接口调用各种外部的数学系统,使得功能十分强大。另外与Latex的协同和嵌入功能,Sage Notebook和SageMathCloud等工具也都做得挺好用的。
我自己不是专业搞数学的,但是感觉开源项目里面要想出一个Matlab、Mathematica或者Maple级别的软件,估计就得靠他了。Sage诞生于2005年,到目前为止国内关注的还很少,可能一方面是因为dao版的Matlab等软件实在太方便了,另一方面因为数学系统本身涉及许多非常专业的数学知识,一般程序员很少接触、专业人士又很少注开源。感觉要是能在大学课程(比如抽象代数、数论等)中得到使用的话会有比较好的普及效果。
对于我自己来说,平时从事计算机视觉和机器学习的研究,大概了解Sage了之后,也发现大部分纯数学的功能自己一般很难用上,其中和我做过的工作比较有关的是有关代数几何中用Groebner basis解多项式方程组的一些东西,不过自己纯是外行,不好说能不能用Sage得到什么结果。写这个介绍还是希望Sage能在国内有所发展,对相关的研究人员有所帮助吧。如果对Sage或者计算机视觉感兴趣,欢迎来访问我的博客cvnote(http://cvnote.info)。
一些参考或相关的链接
官方教程:http://www.sagemath.org/doc/tutorial/index.html
官方中文:http://www.sagemath.org/zh/
国内博客Lainme’s Blog的教程中文翻译,博客上还有一些Sage使用的帖子:http://www.lainme.com/doku.php/topic/sage/start
国内amao博客男单 618的中文教程翻译,博客有很多关于Sage使用的帖子:http://ai7.org/wp/html/682.html