DataStructure - 链表(List,DbList)
数组
说链表前,先来讨论下数组,学过数据结构的人都知道数组是具有随机访问的特点. 比如下面一段程序:
int a[10];
a[2] = 2;
printf("%d\n", *(a+2));
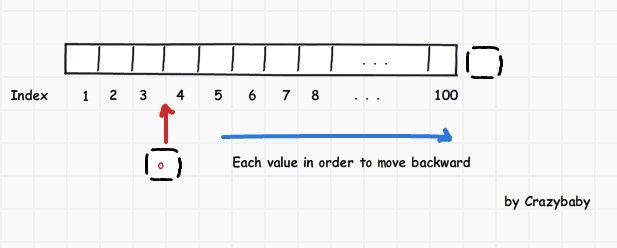
给索引为2的位置初始化一个2, 再通过 a的首地址偏移2*sizeof(int)的大小来随机访问这个地址的值.数组 随机访问的优势也使它 丧失了灵活性插入和删除的功能.比如一个数组空间大小为100(index)*sizeof(char), 我要在第3个index位置插入一个 'o' ,我必须把数组从第100到第4个位置 依次往后移动一个位置
删除数组中一个元素也一样,后面的元素都要往前forward一个位置.这就引来了效率问题,有人说还有个确定是数组在处理一组数据之前必须先确定数组的大小,其实这个可以用malloc来进行动态分配空间的,再通过返回的指向数组的指针来进行使用.所以主要还是插入和删除 ,所以就引申了链表这种数据结构.
单向链表
正如前面所说,数组有两大缺点,插入和删除时需要移动大量元素.而对于链表这是它的优势,所谓链表则是一堆 "链" 起来的元素. 计算机中的数据存储在内存中占用一定内存空间,这个内存空间伴随着也会有相应的地址,就像你的家一样,内存的地址 就像是 你家的地址 可以进行唯一标识. 链表的实现便是利用了数据的地址.
结点
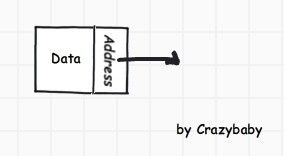
如图所示, Data是数据部分,Address存储的是下一个存储单元的地址. 当计算机对某个数据进行访问后,依据当前结点中的地址便可以找到下一个结点,进而完成对下一个结点中的数据的访问和操作.让我们回头看看插入和删除问题,当需要插入一个结点时,只需要把指针重新指向新的数据,新的数据指向原指针指向的数据即可.删除节点也同样只是改变指针的方向.
表头指针和表尾指针
这里引入这两个指针是为了使链表更方便的进行操作,表头指针指向了链表的第一个节点(又称为表头结点),表尾指针指向链表的最后一个结点.
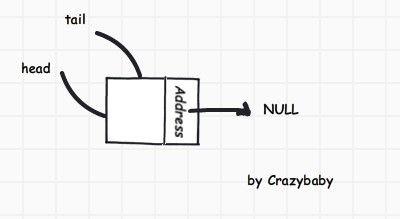
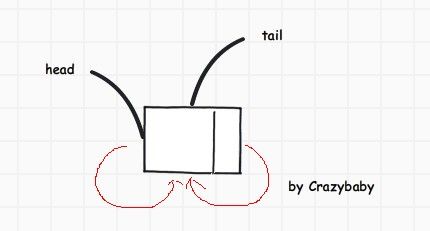
如图所示,这是一个空的单向链表,head和tail分别是表头和表尾指针 .引入头指针是为了方便进行空表和非空表的操作.比如
head->next == NULL; //就是个空表了
引入尾指针是指向链表的最后一个结点,指向为NULL,这样如果最后一个结点为表尾指针则指向NULL,相反也成立. 另外设立表尾指针也是为了在O(1)时间复杂度内 找到尾部.
下面继续深入,拆解链表的各个操作.为了使链表更加灵活,下文会选用C++模板来实现各个操作.
表结点操作构思和实现
节点类构造必须简单,因为属于基础组成部分,复杂不得.所以基本操作有:
1.设置当前节点指针指向的另外一个结点地址
听起来有点拗口,不过指针这东西生来就这样,没办法,大家就将就点吧.下面是实现:
template <class T>
void ListNode<T>::SetLink(ListNode<T>* next) {
link = next;
}
2.取出当前节点的指向地址.
template <class T>
ListNode<T>* ListNode<T>::GetLink() {
return link;
}
3.取出当前节点的数据部分
template <class T>
T& ListNode<T>::GetData() {
return data;
}
这样基本表结点就设计好了.
单向链表操作-末尾插入结点
正因为有了尾结点,向末尾插入就方便多了.直接在末尾指针后面new一个结点加入即可.
template <class T>
bool List<T>::TailAddNode(T value) {
ListNode<T>* add = new ListNode<T>(value);
tail->SetLink(add);
tail = tail->GetLink(); /**< 再让尾指针指向新的尾部 */
tail->SetLink(NULL);
if (NULL != tail) {
return TRUE;
}
else
{
return FALSE;
}
}
单向链表操作-任意索引位置插入新结点
任意位置插入新结点需要先知道插入的索引位置和值, 知道索引位置后,需要先 遍历 到索引位置,再进行指针置换操作.
在程序设计时,为了程序健壮性,在传入的索引值时需要先机型条件限制:
index > 0 && index < 总结点数 - 1
然后遍历到索引位置:
ListNode<T>* cur = head;
while (index) {
cur= cur->GetLink();
index--;
}
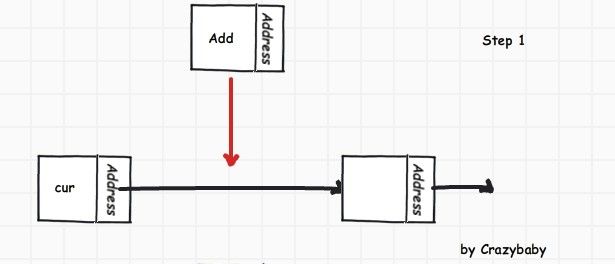
取出cur后,下面就类似像尾结点插入新结点的思路差不多.
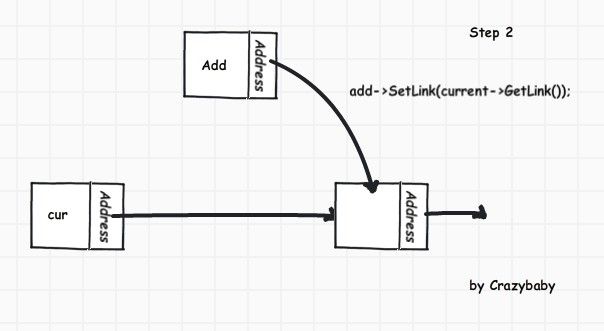
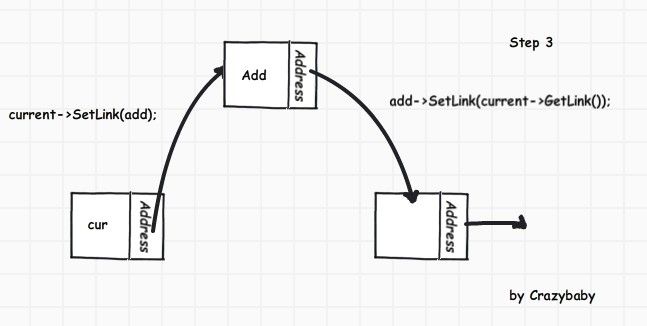
ListNode<T>* add = new ListNode<T>(value);
add->SetLink(cur->GetLink());
cur->SetLink(add);
if (cur->GetLink()!=NULL) {
return TRUE;
}
else
{
return FALSE;
}再用图分解下各个操作:
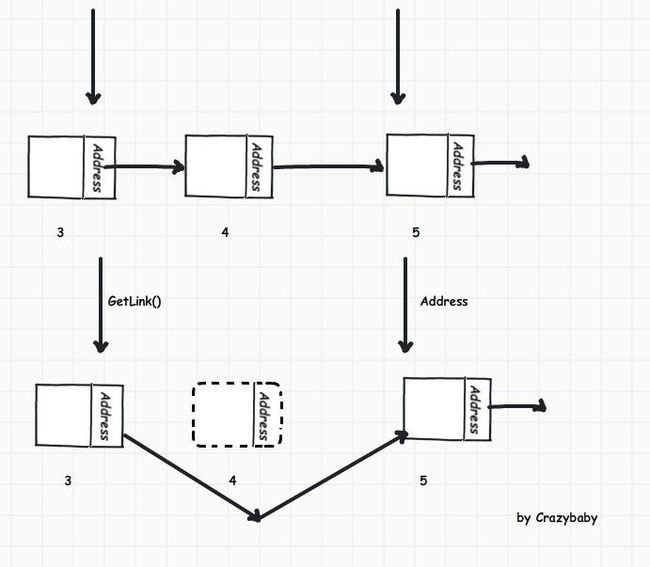
单向链表操作-删除任意节点
如图所示,删除index=4的结点必须先得知 3 结点.所以需要个指针来指向前一个结点. 删除结点同样需要进行 index 条件限制.
index > 0 && index < 总结点数 - 1
取出3结点和当前结点
ListNode<T>* preNode = head; //前一结点
ListNode<T>* curNode = head->GetLink(); //当前结点
while (index) {
preNode = preNode->GetLink();
curNode = curNode->GetLink();
index--;
}
再进行指针操作:
preNode->SetLink(curNode->GetLink());
另外需要想到的是 如果删除的是最后一个结点,需要把尾指针(也即 tail)置到新结点.
if (tail == curNode) { tail = preNode; }
单向链表操作-链表清空
删除所有结点,需要对链表进行一次遍历,如果每个结点是malloc的还需要注意内存泄漏问题,也即每个结点都要进行free操作.
ListNode<T>* cur;
while (head->GetLink()!=NULL) {
cur = head->GetLink();
head->SetLink(cur->GetLink()); //当前指向的结点赋给头结点
delete cur;
}
链表操作-链表判空
链表判空,前面已经说过,只要根据头指针来判断就可以了 也即
head->GetLink() == NULL;
单向链表操作-链表结点数
还是需要进行一次遍历,从多次操作我们可以看出 链表不支持随机访问操作.
template <class T>
int List<T>::GetCount() {
int count = 0;
ListNode<T>* cur= head->GetLink();
while (NULL != cur) {
count++;
cur = cur->GetLink();
}
return count;
}
基础链表的基本操作基本上就这几个,下面继续深入下去,谈谈双向链表.
双向链表
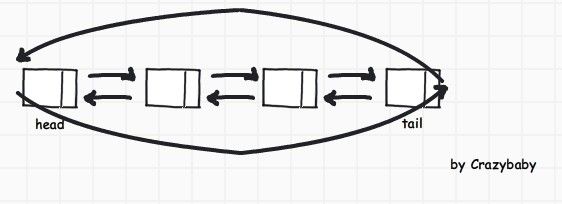
在上面我们可以看出,若需要获取一个结点的前驱结点是很麻烦的,如果我们在每个节点中同时保存 指向前面结点的指针 和 指向后面的指针, 那么时间复杂度将大大降低.O(1)
双向链表和单向链表类似,不同的是除了每个节点多了一个指向前面结点的指针外,链表的最后一个结点也包括一个指针, 一个指向前面一个结点,还有一个指向头结点.
之前的链表结点类中需要增加两个API ,一个是设置前驱结点的 , 还有一个是取前驱结点的
/* --- 设置前驱结点 --- */
template <class T>
void ListNode<T>::SetPrior(ListNode<T>* pre) {
prior = pre;
}
/* --- 取前驱结点 --- */
template <class T>
ListNode<T>* ListNode<T>::GetPrior() {
return prior;
}
现在的结点看起来会是这样子
双向链表的基本操作有点复杂,因为改变的指针操作比之前会多一倍.
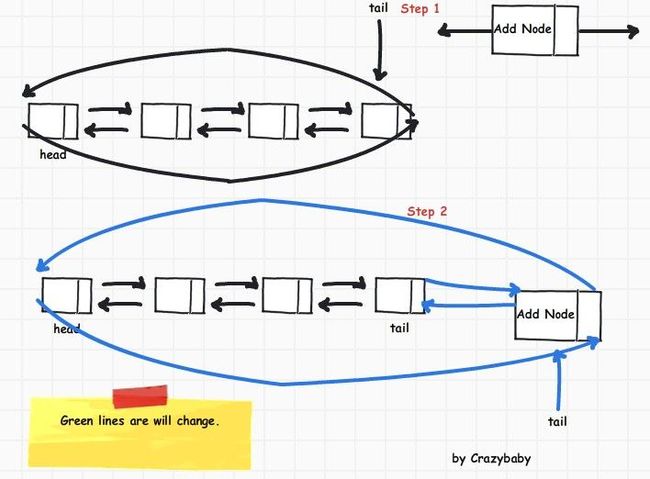
双向链表-增加结点
这是向链表尾部插入结点,包括尾指针总共需要改变 5 个指针.
如果不在尾部插入,也就没有尾指针的事了,只需要改变 4 个指针./*!
\@bref Add node to list tail
\@input T value
\@return bool
*/
template <class T>
bool DoubleList<T>::AddTail(T value) {
DoubleListNode<T>* add = new DoubleListNode<T>(value);
tail->SetLink(add);
add->SetLink(tail); /**< 设置前驱指针 */
tail = tail->GetLink();
tail->SetLink(head); /**< 设置尾结点指向那个head */
head->SetPrior(add); /**< 重新设置head的前驱 */
/* --- 成功处理 --- */
if (NULL != tail) {
return TRUE;
}
else
{
return FALSE;
}
}
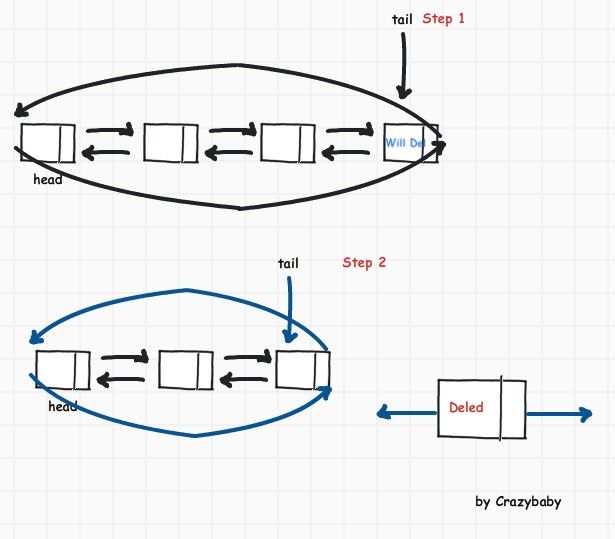
双向链表-删除结点
删除尾巴结点
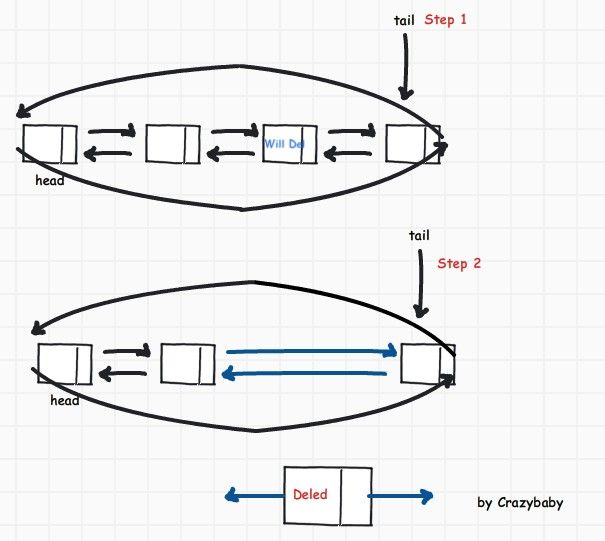
下面为删除中间结点
删除任意结点还是和单向链表一样 需要个指针保存前驱结点. 另外保存当前结点的指针改为指向后继结点的指针.
DoubleListNode<T>* preNode = cur->GetLink(); DoubleListNode<T>* nextNode = cur->GetLink(); preNode->GetLink(cur->GetLink()); nextNode->GetLink(cur->GetPrior());
除了删除和插入,其它操作都差不多了,另外查询比单向链表查询会方便些,因为了前驱指针的加入.可以双向进行查询. 虽说增加一个域方便了,其实也同时增加了空间的需求,也使得插入和删除的开销增加了一倍,因为有更多的指针需要定位.
最后总结下需要注意的问题:
1.链表操作要注意指针的初始化问题,不然会出现经典的Segmentation Violation 和 Memmory Access violation的结果
2.程序实现时需要注意索引的有效性 index>0 && index< 总结点数-头结点(1)
3.当链表结点信息中的数据部分包含malloc的数据时,删除结点需要注意free / delete .不然Memory Leak问题会等着你
原文链接: http://blog.csdn.net/crazyjixiang/article/details/6746898