计数排序与位图排序

　　计数排序(Counting sort)是一种稳定的线性时间排序算法。计数排序使用一个额外的数组C，其中第i个元素是待排序数组A中值等于i的元素的个数。然后根据数组C来将A中的元素排到正确的位置。计数排序不是比较排序，排序的速度快于任何比较排序算法。由于用来计数的数组C的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。计数排序更适合于小范围集合的排序。比如100万学生参加高考，我们想对这100万学生的数学成绩（假设分数为0到100）做个排序。计数排序的步骤如下：

1. 确定待排序数组中数值的范围，以此确定C数组的大小；
2. 计算数组中每个值为A[i]的元素出现的次数，存入数组C[A[i]]中；
3. 用C数组重新填充原数组。

　　计数排序的实现代码如下，需要注意的是代码并未对数组内的元素进行比较，而是：

 1 void CountingSort(int *nArray, int nSize)  2 {  3     int *nCounting = new int[nSize];        //nCounting 是一个伴随数组，记录原数组中每个数出现的次数 
 4     memset(nCounting, 0x0, sizeof(int)*nSize);  5  
 6     int i;  7     for(i=0; i!=nSize; i++)  8         nCounting[nArray[i]]++;     //计算每个数出现过的次数，例如 nCounting[5] = 3;表示原数组存在3个5 
 9  
10     int z=0; 11     for(i=0; i<=nSize; i++) 12  { 13         while(nCounting[i]-- > 0)    //nCounting[i]>0 表示原数组中存在数字i 
14             nArray[z++] = i; 15  } 16  
17  delete[] nCounting; 18 
19     return; 20 }

　　代码很好理解，但是仍然需要注意几点：

1. 计数排序是典型的以空间换时间，数组内元素的范围决定了伴随数组C的大小，从而决定程序运行的时间和内存大小。
2. 计算C[i]时，使用了A[i]作为下标，那么必须保证A数组中所有元素非负，如果存在负值，那么可以对数组元素加上最小负值的绝对值，使得数组元素全部为正数。

---

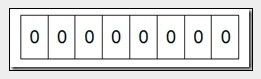
　　当计数排序中原数组A中数值范围较大时，伴随数组C也越大，内存的消耗越大，要进一步限制内存的大小，可以使用位图法（Bit-map）进行排序。假设要对数值范围为0-7内的5个数(4,7,2,5,3)进行排序，那么我们就可以采用Bit-map的方法来达到排序的目的。要表示8个数，我们就只需要8个Bit（1Bytes），首先我们开辟1Byte的空间，将这些空间的所有Bit位都置为0，如下图

　　    　

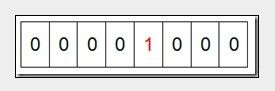
然后遍历这5个元素，首先第一个元素是4，那么就把4对应的位置为1，当然了这里的操作涉及到Big-ending和Little-ending的情况，这里默认为Big-ending），因为是从零开始的，所以要把第五位置为一（如下图）：

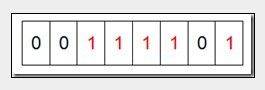
接着再处理第二个元素7，将第八位置为1,，接着再处理第三个元素，一直到最后处理完所有的元素，将相应的位置为1，这时候的内存的Bit位的状态如下：

最后我们现在遍历一遍Bit区域，将该位是一的位的编号输出（2，3，4，5，7），这样就达到了排序的目的。以上文字摘自http://www.cnblogs.com/Trony/archive/2012/09/01/2667064.html

实现如下：

 1 void SetBit(char *pData, int nNum)  2 {  3     //找出需要设置的字节位置
 4     for(int i=0; i<nNum/BYTESIZE; i++)  5         pData++;  6     //对字节中nNum对应的bit位进行设置
 7     *(pData) |= 0x1<<(nNum%BYTESIZE);  8 }  9 
10 void BitMapSort(int Arr[], int nSize) 11 { 12     //一个byte可以表示8个bit，伴随数组的大小为(nSize/BYTESIZE)+1
13     char *pData = new char[nSize/BYTESIZE+1]; 14     memset(pData, 0x0, sizeof(char)*(nSize/BYTESIZE+1)); 15     
16     //根据原数组中每个元素的值设置伴随数组中对应的bit位
17     for(int i=0; i!=nSize; i++) 18  SetBit(pData, Arr[i]); 19 
20     int z=0; 21     for(int i=0; i!=nSize/BYTESIZE+1; i++) 22  { 23         //对每个byte中的8个bit进行校验
24         for(int j=0; j!=BYTESIZE; j++) 25  { 26             if(*pData & (0x1<<j)) 27                 Arr[z++] = i*BYTESIZE+j; 28  } 29         pData++; 30  } 31 
32  delete[] pData; 33 } 34 
35 int _tmain(int argc, _TCHAR* argv[]) 36 { 37     int a[] = {3,1,2,5,9}; 38 
39     BitMapSort(a, sizeof(a)/sizeof(*a)); 40     for(int i=0; i!=sizeof(a)/sizeof(*a); i++) 41         cout<<a[i]<<"    "; 42     cout<<endl; 43     return 0; 44 }

　　位图排序同样是一种线性排序，与计数排序相比，动态分配的伴随数组占用的空间小了很多，但是存在一个缺点，位图排序要求所排序的数组中没有重复元素，因为一个bit位只能用0,1来表示一个整数的存在与否，不能表示此整数数的出现次数，位图排序用到了很多位操作，代码实现也比计数排序更为复杂。

　　位图法除了可以用作排序，也可以用来做匹配和查找。这里举一个字符串包含（匹配）的例子：

 1 bool bMatchString(const char *a, const char *b)  2 {  3     int nDictionary = 0;  4     int nLenA = strlen(a), nLenB = strlen(b);  5 
 6     int i;  7     for(i=0; i!=nLenA; i++)  8         nDictionary |= 0x1<<(a[i]-'A');    //对应的bit位进行set
 9 
10     for(i=0; i!=nLenB; i++) 11         if(!(nDictionary & 1<<(b[i]-'A'))) 12             break; 13 
14     if(i != nLenB) 15         return false; 16     else
17         return true; 18 } 19 
20 int _tmain(int argc, _TCHAR* argv[]) 21 { 22     char A[] = "YOUKNOWILVEYOUSO"; 23     char B[] = "LOVE"; 24 
25     if(bMatchString(A, B)) 26         cout<<"A has B"<<endl; 27 
28     return 0; 29 }

　　实际上对于字符串匹配（包含）程序，定义int hash[26]的伴随数组即可（将元素范围看做26个字母），不会有太多内存消耗，这里只是为了说明位图法同样适用。