【博弈专题】解题报告

HDU1079 Calendar Game

　　设k=m+d，容易知道，终态2001.11.4为P局面（后手胜），此时k=11+4=15，为奇态。我们不妨假设：如果k为寄态，先手胜；k为偶态，后手胜。对于一年中某个日子，其后一天或者下个月同一天都是k的奇偶转换，对于先手来说，如果此时k为奇态，则必胜；如果为偶态，则看是否能给后手也留下一个偶态让其处于N局面（先手胜）。一年中可以偶态到偶态的日子只有4个：4.30、6.30、9.30、11.30。这4个日子虽然k为偶数，但也属于先手胜局面，因为这四个日子能给对方留下k偶态。

#include <stdio.h>
#include <string.h>

int main()
{
    int y, m, d, t;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d%d%d", &y, &m, &d);
        int k = m + d;
        if(((m==4||m==6||m==9||m==11)&&d==30)||k % 2 == 0)
            puts("YES");
        else
            puts("NO");
    }
    return 0;
}

View Code

 

HDU1564 Play a game

　　n为偶数则8600胜，n为奇数则ailyanlu胜。

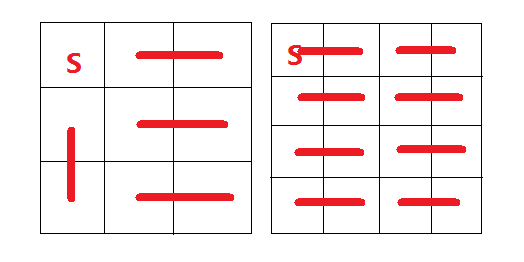
证明：如下图

　　对于两个图，我们用1x2的矩形进行覆盖，当一个人走到一个新的1x2方块时，另一个人为必胜者，因为他总可以走该方块的另一个格子。

#include <stdio.h>
#include <string.h>

int main()
{
    int x;
    while(scanf("%d", &x) != EOF && x)
    {
        if(x % 2 == 0)
            puts("8600");
        else
            puts("ailyanlu");
    }
    return 0;
}

View Code

 

HDU1846 Brave Game

　　最经典的取石子游戏了，当“n==k*(m+1)(k为整数)”成立时，为后手胜局面，其他局面为先手胜局面。分析从略。

#include <stdio.h>
#include <string.h>

int main()
{
    int t, n, m;
    scanf("%d", &t);
    while(t--)
    {
        scanf("%d%d", &n, &m);
        if(n % (m+1) == 0)
            puts("second");
        else
            puts("first");
    }
    return 0;
}

View Code

 

HDOJ1847 Good Luck in CET-4 Everybody!

　　直接手动打表“1 1 0 1 1 0 1 1 0 1 1 0...”，当n为3的倍数时后手胜，其他情况为先手胜。

#include <stdio.h>
#include <string.h>

int f[1005];

void init()
{
    for(int i = 1; i <= 1000; i++)
        f[i] = !((i % 3) == 0);
}

int main()
{
    int n;
    init();
    while(scanf("%d", &n) != EOF)
        printf("%s\n", f[n] ? "Kiki" : "Cici");
    return 0;
}

View Code

 

HDOJ2147 kiki's game

　　棋盘中能向左、向下或左下方移动，那么谁先到达左下角位置，谁就赢了。

　　这道题我是逐步逐行推导的：

　　1. 如果棋盘只有一行，那么胜负由列数的奇偶性判断；

　　2. 如果棋盘有两行，则先手必胜，证明如下：

　　　　设起始点为s，s左下方的格子为k，先手可以控制谁到达k（让自己到达k的话直接一步到k，让对方到达k的话向下走而对方必须向左走）。证毕。

　　那么，我们可以推导出一个这样的胜负图：

...	...	...	...	...	...
1	1	1	1	1	...
0	1	0	1	0	...
1	1	1	1	1	...
0	1	0	1	0	...

　　格子中0表示后手胜，1表示先手胜。

#include <stdio.h>
#include <string.h>

int main()
{
    int n, m;
    while(scanf("%d%d", &n, &m) != EOF && n + m)
    {
        if((n % 2 == 0) || ((n % 2 == 1) && (m % 2 == 0)))
            puts("Wonderful!");
        else
            puts("What a pity!");
    }
    return 0;
}

View Code

 

HDU2516 取石子游戏

　　一直推，多推几个，发现规律了吗？没错，就是斐波那契数列。

#include <stdio.h>
#include <string.h>
#define N 45
int f[N];

void init()
{
    f[1] = 2;
    f[2] = 3;
    for(int i = 3; i < N; i++)
        f[i] = f[i-1] + f[i-2];
}

int main()
{
    int n;
    init();
    while(scanf("%d", &n) != EOF && n)
    {
        bool flag = false;
        for(int i = 1; i < N; i++)
        {
            if(f[i] == n)
            {
                flag = true;
                break;
            }
            if(n < f[i])
                break;
        }
        if(flag) puts("Second win");
        else puts("First win");
    }
    return 0;
}

View Code

 

HDU2897 邂逅明下

　　把(p+q)作为一个单位，因为假如一个人取x个，另外一个人总可以取y个使得（x+y）== （p+q）。设k=n%(p+q)，那么我们只需要判断k的情况下的胜负情况。不难推出当1<=k<=p时先手负，其他局面都是先手胜。

#include <stdio.h>
#include <string.h>

int main()
{
    int n, p, q;
    while(scanf("%d%d%d", &n, &p, &q) != EOF)
    {
        int k = n % (p + q);
        if(k != 0 && k <= p)
            puts("LOST");
        else
            puts("WIN");
    }
    return 0;
}

View Code

 

POJ1740 A New Stone Game

　　楼教男人八题中的博弈题。一步一步分析下来就不难了。

　　1. 如果只有一堆，先手可以全部拿完然后胜利；

　　2. 如果有两堆，石子数分别为x和y，那么

　　　　1) 当x==y时，先手负，因为后手可以和先手作出同样的动作；

　　　　2) 当x!=y时，先手胜，因为先手可以再x和y中大的那一堆石子取出k颗使得x==y，也就是让后手来面对必败局面；

　　3. 如果有三堆，石子数分别为x，y，z，那么

　　　　1) 当x，y，z中至少有两个是相等的时候，先手胜，因为先手可以取走一堆石子使得剩下的两堆石子数相等，那么情况就如同1

　　　　2) 当x，y，z互不相等时，不妨设x < y < z，那么我们在z中取走z-(y-x)颗石子，然后将剩下的y-x颗石子放到x堆里，此时有(y, y)的两堆石子，那么情况如2

　　综上所述，只有在石子的堆数为偶数且石子数两个两个相等情况下，先手负，其他局面都是先手胜局面。

#include <stdio.h>
#include <string.h>
#include <algorithm>

int a[105];

int main()
{
    int n;
    while(scanf("%d", &n) != EOF && n)
    {
        for(int i = 0; i < n; i++)
            scanf("%d", &a[i]);
        if(n & 1) 
        {
            puts("1");
            continue;
        }
        std::sort(a, a+n);
        bool flag = false;
        for(int i = 0; i < n; i+=2)
        {
            if(a[i] != a[i+1])
            {
                flag = true;
                break;
            }
        }
        printf("%d\n", flag);
    }
    return 0;
}

View Code