2012 Multi-University Training Contest 1
解题报告:
这道题问的就是将1个串如何变为stringA+stringB的形式,使得stringA是stringB经过映射得到相同的串。映射那步其实没有什么价值,假设str为原串s经过 映射后得到的串,我们可以以str为模式串,以s为原串做一次扩展KMP,得到extend数组,extend[i]表示原串以第i开始与模式串的前缀的最长匹配。经过O(n) 的枚举,我们可以得到:
若extend[i]+i=len且i>=extend[i]时,表示stringB即为该点之前的s串,stringA即为该点之前的str串,最后输出即可。
扩展kmp的资料很少,比较经典的是刘雅琼的这个课件了。
#include <stdio.h> #include <string.h> #include <map> #define maxn 200000 using namespace std; map<char, char>map1; inline int max(int x,int y){return x > y ? x : y;} char s[maxn], tab[maxn], c[maxn]; int next[maxn], extend[maxn]; void EKMP(char s[], char t[]) //s[]为主串,t[]为模版串 { int i, j, p, l; int len = strlen(t); int len1 = strlen(s); memset(next, 0, sizeof(next)); memset(extend, 0, sizeof(extend)); next[0] = len; j = 0; while(1 + j < len && t[j] == t[1 + j]) j ++; next[1]=j; int a = 1; for(i = 2;i < len; i++) { p = next[a] + a - 1; l = next[i - a]; if(i + l <= p) next[i] = l; else { j = max(0, p - i + 1); while(i + j < len && t[i + j] == t[j]) j ++; next[i] = j, a = i; } } j = 0; while(j < len1 && j < len && s[j] == t[j]) j ++; extend[0]=j; a = 0; for(i = 1; i < len1; i ++) { p = extend[a] + a - 1; l = next[i - a]; if(l + i <= p) extend[i] = next[i - a]; else { j=max(0, p - i + 1); while(i + j < len1 && j < len && s[i + j] == t[j]) j ++; extend[i] = j, a = i; } } } int main() { int i, j; int t; scanf("%d", &t); while(t --) { scanf("%s%s", tab, s); int len = strlen(tab); int len1 = strlen(s); for(i = 0; i < len; i ++) map1[tab[i]] = 'a' + i; for(i = 0 ; i < len1; i ++) c[i] = map1[s[i]]; c[i] = '\0'; EKMP(s, c); for(i = 0; i < len1; i ++) if(i + extend[i] >= len1 && i >= extend[i]) break; for(j = 0; j < i; j ++)printf("%c", s[j]); for(j = 0; j < i; j ++)printf("%c", map1[s[j]]); printf("\n"); } return 0; }
很强悍的动态规划。各种情况递推得要仔细,下面是来自官方的解题报告:
状态表示 f[i][0][j]:前i行已经出现了j部分且第i行的两个格子属于同一部分的方法数
f[i][1][j]:前i行已经出现了j部分且第i行的两个格子属于不同部分的方法数
初始条件 f[1][0][1]=f[1][1][2]=1
状态转移 f[i+1][0][j]=(f[i+1][0][j]+f[i][0][j]+f[i][1][j]*2)%mod;
f[i+1][0][j+1]=(f[i+1][0][j+1]+f[i][0][j]+f[i][1][j])%mod;
f[i+1][1][j]=(f[i+1][1][j]+f[i][1][j])%mod;
f[i+1][1][j+1]=(f[i+1][1][j+1]+f[i][0][j]*2+f[i][1][j]*2)%mod;
f[i+1][1][j+2]=(f[i+1][1][j+2]+f[i][0][j]+f[i][1][j])%mod;
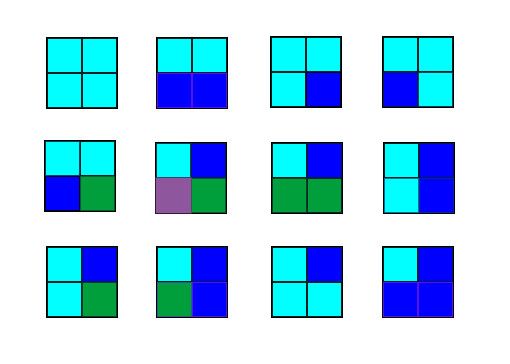
共12种不同的状态转移(见下图)
1 #include <stdio.h> 2 #include <string.h> 3 #define mod 100000007 4 int f[1005][2][2005]; 5 int n, k; 6 void init() 7 { 8 int i, j; 9 f[1][0][1] = f[1][1][2] = 1; 10 11 for(i = 1; i < 1001; i ++) 12 { 13 for(j = 1; j <= i * 2; j ++) 14 { 15 f[i+1][0][j]=(f[i+1][0][j]+f[i][0][j]+f[i][1][j]*2)%mod; 16 17 f[i+1][0][j+1]=(f[i+1][0][j+1]+f[i][0][j]+f[i][1][j])%mod; 18 19 f[i+1][1][j]=(f[i+1][1][j]+f[i][1][j])%mod; 20 21 f[i+1][1][j+1]=(f[i+1][1][j+1]+f[i][0][j]*2+f[i][1][j]*2)%mod; 22 23 f[i+1][1][j+2]=(f[i+1][1][j+2]+f[i][0][j]+f[i][1][j])%mod; 24 } 25 } 26 } 27 28 int main() 29 { 30 init(); 31 int t; 32 scanf("%d", &t); 33 while(t --) 34 { 35 scanf("%d%d", &n, &k); 36 printf("%d\n", (f[n][0][k] + f[n][1][k]) % mod); 37 } 38 return 0; 39 }