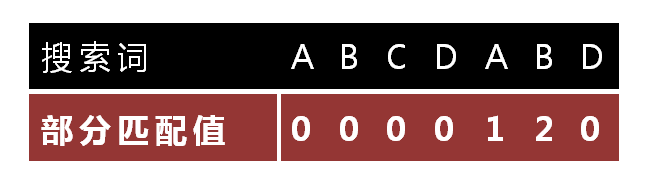字符串匹配的KMP算法详解及C#实现

字符串面试题系列之七：字符串全排列

编译环境

   本系列文章所提供的算法均在以下环境下编译通过。

【算法编译环境】Federa 8，linux 2.6.35.6-45.fc14.i686 
【处理器】 Intel(R) Core(TM)2 Quad CPU Q9400 @ 2.66GHz 
【内存】 2025272 kB

前言

    这是一道排列组合的题目。对于排列组合的题目在面试当中也是十分常见，主要考察小伙伴们的思维的有序性和解决问题的能力。本题就曾出自腾讯的笔试当中。一般这类题目大家做的时候用树的方式来帮助思考会有一些效果。

    本系列文章均系笔者所写,难免有一些错误或者纰漏，如果小伙伴们有好的建议或者更好的算法，请不吝赐教。

正文

【题目】

   输入一个字符串，打印出该字符串中字符的所有排列。

【例子】

   输入字符串abc，则输出由字符a、b、c所能排列出来的所有字符串abc、acb、bac、bca、cab和cba。

【分析】

   这是一道排列组合的题目。而做排列组合的时候头脑要保持清醒并且有序。我们列举一个例子，假设有字符串abc，如果我们手动排列，过程是怎样的呢？

   一般人的分析习惯总是把大问题化成小问题来解决。这是我们的习惯。
首先保持a在第一位不动，我们看子字符串bc，bc的排列是bc和cb，这样我们得到结果是abc,acb ; 
其次保持b在第一位不东，我们看子字符串ac，ac的排列是ac和ca，这样我们得到结果是bac,bca ;
再次保持c在第一位不东，我们看子字符串ab，ab的排列是ab和ba，这样我们得到结果是cab,cba 。
这样我们都得到三个字符的排列是abc,acb,bac,bca,cab,cba。这样思维是不是很清晰。

   参照上面的手工做法，我们如何用程序去实现呢。显然用递归的方式更符合我们的思维。

第一步：当字符串只有1个字符的时候，其排列是字符本身。
第二步：递归求出子字符串的排列
第三步：算法结束。

【代码】

#include <iostream>
#include <cstring>

#define swap(a, b) { char c=a; a=b; b=c; }

void string_permutation( char * const string, int start, int end )
{
   if( start == end )
   {
      std::cout << string << std::endl;
   }
   else
   {
      for( int i = start; i < end; i++)
      {
         // swap two characters
         swap( string[i], string[start] );
         string_permutation( string, start + 1, end );
         // recover
         swap( string[i], string[start] );
      }
   }
}

int main( int argc, char ** argv )
{
   char string[] = "abcd";
   string_permutation( string, 0, strlen(string) );
   return 0;
}

【结论】

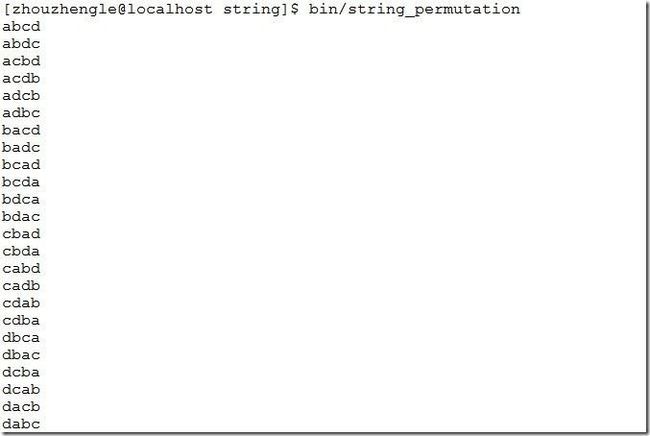
   我们输入字符串abcd，应该有16种排列组合的方式。得到的结果如下：

作者

   出处：http://www.cnblogs.com/gina

   本文版权归作者所有，欢迎转载，但未经作者同意必须保留此段声明，且在文章页面明显位置给出原文连接，否则保留追究法律责任的权利。

 

 

分类:  坑爹的面试题

标签:  字符串面试

字符串匹配的KMP算法详解及C#实现

字符串匹配是计算机的基本任务之一。

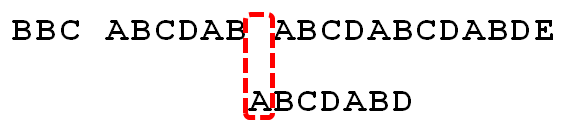
　　举例来说，有一个字符串"BBC ABCDAB ABCDABCDABDE"，我想知道，里面是否包含另一个字符串"ABCDABD"？许多算法可以完成这个任务，Knuth-Morris-Pratt算法（简称KMP）是最常用的之一。它以三个发明者命名，起头的那个K就是著名科学家Donald Knuth。

      这种算法不太容易理解，网上有很多解释，但读起来都很费劲。直到读到Jake Boxer的文章，我才真正理解这种算法。下面，我用自己的语言，试图写一篇比较好懂的KMP算法解释。

      1.

　　首先，字符串"BBC ABCDAB ABCDABCDABDE"的第一个字符与搜索词"ABCDABD"的第一个字符，进行比较。因为B与A不匹配，所以搜索词后移一位。

　　2.

　　因为B与A不匹配，搜索词再往后移。

　　3.

　　就这样，直到字符串有一个字符，与搜索词的第一个字符相同为止。

　　4.

　　接着比较字符串和搜索词的下一个字符，还是相同。

　　5.

　　直到字符串有一个字符，与搜索词对应的字符不相同为止。

　　6.

　　这时，最自然的反应是，将搜索词整个后移一位，再从头逐个比较。这样做虽然可行，但是效率很差，因为你要把"搜索位置"移到已经比较过的位置，重比一遍。

　　7.

　　一个基本事实是，当空格与D不匹配时，你其实知道前面六个字符是"ABCDAB"。KMP算法的想法是，设法利用这个已知信息，不要把"搜索位置"移回已经比较过的位置，继续把它向后移，这样就提高了效率。

　　8.

　　怎么做到这一点呢？可以针对搜索词，算出一张《部分匹配表》（Partial Match Table）。这张表是如何产生的，后面再介绍，这里只要会用就可以了。

　　9.

　　已知空格与D不匹配时，前面六个字符"ABCDAB"是匹配的。查表可知，最后一个匹配字符B对应的"部分匹配值"为2，因此按照下面的公式算出向后移动的位数：

　　移动位数 = 已匹配的字符数 - 对应的部分匹配值

　　因为 6 - 2 等于4，所以将搜索词向后移动4位。

　　10.

　　因为空格与Ｃ不匹配，搜索词还要继续往后移。这时，已匹配的字符数为2（"AB"），对应的"部分匹配值"为0。所以，移动位数 = 2 - 0，结果为 2，于是将搜索词向后移2位。

　　11.

　　因为空格与A不匹配，继续后移一位。

　　12.

　　逐位比较，直到发现C与D不匹配。于是，移动位数 = 6 - 2，继续将搜索词向后移动4位。

　　13.

　　逐位比较，直到搜索词的最后一位，发现完全匹配，于是搜索完成。如果还要继续搜索（即找出全部匹配），移动位数 = 7 - 0，再将搜索词向后移动7位，这里就不再重复了。

　　14.

　　下面介绍《部分匹配表》是如何产生的。

　　首先，要了解两个概念："前缀"和"后缀"。 "前缀"指除了最后一个字符以外，一个字符串的全部头部组合；"后缀"指除了第一个字符以外，一个字符串的全部尾部组合。

　　15.

　　"部分匹配值"就是"前缀"和"后缀"的最长的共有元素的长度。以"ABCDABD"为例，

　　－　"A"的前缀和后缀都为空集，共有元素的长度为0；

　　－　"AB"的前缀为[A]，后缀为[B]，共有元素的长度为0；

　　－　"ABC"的前缀为[A, AB]，后缀为[BC, C]，共有元素的长度0；

　　－　"ABCD"的前缀为[A, AB, ABC]，后缀为[BCD, CD, D]，共有元素的长度为0；

　　－　"ABCDA"的前缀为[A, AB, ABC, ABCD]，后缀为[BCDA, CDA, DA, A]，共有元素为"A"，长度为1；

　　－　"ABCDAB"的前缀为[A, AB, ABC, ABCD, ABCDA]，后缀为[BCDAB, CDAB, DAB, AB, B]，共有元素为"AB"，长度为2；

　　－　"ABCDABD"的前缀为[A, AB, ABC, ABCD, ABCDA, ABCDAB]，后缀为[BCDABD, CDABD, DABD, ABD, BD, D]，共有元素的长度为0。

　　16.

　　"部分匹配"的实质是，有时候，字符串头部和尾部会有重复。比如，"ABCDAB"之中有两个"AB"，那么它的"部分匹配值"就是2（"AB"的长度）。搜索词移动的时候，第一个"AB"向后移动4位（字符串长度-部分匹配值），就可以来到第二个"AB"的位置。

以上 KMP算法的分析 原文地址：http://www.admin10000.com/document/1974.html

下面是我用C#实现上述分析：

 

  View Code

/// <summary>
/// KMP算法查找字符串
/// </summary>
/// <param name="operateStr">操作字符串</param>
/// <param name="findStr">要查找的字符串</param>
/// <returns>字符串第一次出现的位置索引</returns>
public static int Arithmetic_KMP(string operateStr, string findStr)
{
int index = -1; //正确匹配的开始索引
int[] tableValue = GetPartialMatchTable(findStr);
int i = 0, j = 0; //操作字符串和匹配字符串 索引迭代
while (i < operateStr.Length && j < findStr.Length)
{
if (operateStr[i] == findStr[j]) //当第一个字符匹配上，接着匹配第二、、、
{
if (j == 0) index = i; //记录第一个匹配字符的索引
j++;
i++;
}
else //当没有匹配上的时候
{
if (j == 0) //如果第一个字符就没匹配上
{
i += j + 1 - tableValue[j]; //移动位数 =已匹配的字符数 - 对应的部分匹配值
}
else
{
i = index + j - tableValue[j - 1]; //如果已匹配的字符数不为零，则重新定义i迭代
}
j = 0; //将已匹配迭代置为0
}
}
return index;
}
/// <summary>
/// 产生 部分匹配表
/// </summary>
/// <param name="str">要查找匹配的字符串</param>
/// <returns></returns>
public static int[] GetPartialMatchTable(string str)
{
string[] left, right; //前缀、后缀
int[] result = new int[str.Length]; //保存 部分匹配表
for (int i = 0; i < str.Length; i++)
{
left = new string[i]; //实例化前缀 容器
right = new string[i]; //实例化后缀容器
//前缀
for (int j = 0; j < i; j++)
{
if (j == 0)
left[j] = str[j].ToString();
else
left[j] = left[j - 1] + str[j].ToString();
}
//后缀
for (int k = i; k > 0; k--)
{
if (k == i)
right[k - 1] = str[k].ToString();
else
right[k - 1] = str[k].ToString() + right[k];
}
//找到前缀和后缀中相同的项，长度即为相等项的长度（相等项应该只有一项）
int num = left.Length - 1;
for (int m = 0; m < left.Length; m++)
{
if (right[num] == left[m])
{
result[i] = left[m].Length;
}
num--;
}
}
return result;
}

 

如果要查询出匹配字符串出现的所有位置，可以使用递推来循环查找，代码如下：

  View Code

/// <summary>
/// 尾递归查询出 字符串出现的所有开始索引
/// </summary>
/// <param name="str1">操作字符串</param>
/// <param name="str2">要查找的字符串</param>
/// <param name="indexs">位置索引 集合</param>
public static void Search(string str1, string str2, IList<int> indexs)
{
int index = Arithmetic_KMP(str1, str2);
int temp = index;
if (indexs.Count > 0)
{
index += indexs[indexs.Count - 1] + str2.Length;
}
indexs.Add(index);
if (temp + (str2.Length - 1) * 2 <= str1.Length)
Search(str1.Substring(temp + str2.Length), str2, indexs);
}

这是我看了KMP算法解析后，用C#代码实现的。如有不足之处，请指出，谢谢！还有其他朋友的实现，代码如下：

  View Code

private static int KmpIndexOf(string s, string t)
{
int i = 0, j = 0, v;
int[] nextVal = GetNextVal(t);

while (i < s.Length && j < t.Length)
{
if (j == -1 || s[i] == t[j])
{
i++;
j++;
}
else
{
j = nextVal[j];
}
}

if (j >= t.Length)
v = i - t.Length;
else
v = -1;

return v;
}

 

private static int[] GetNextVal(string t)
{
int j = 0, k = -1;
int[] nextVal = new int[t.Length];

nextVal[0] = -1;

while (j < t.Length - 1)
{
if (k == -1 || t[j] == t[k])
{
j++;
k++;
if (t[j] != t[k])
{
nextVal[j] = k;
}
else
{
nextVal[j] = nextVal[k];
}
}
else
{
k = nextVal[k];
}
}

return nextVal;
}

 

这种实现比我上面的实现，性能要高出三倍，原因在与，它生成“Next特征数组”（网上有资料这么叫的）只用了一个循环，而我的用了三个循环，貌似最后那个数组值也不一样，没看懂他的思路是怎么回事，如有懂的，请指点下，谢谢！测试代码下载：http://files.cnblogs.com/joey0210/ArithmeticSolution.rar

 

 

 

分类:  C#,  算法

标签:  KMP算法