学习凸包(四):Graham 扫描法
Graham扫描法
基本思想:通过设置一个关于候选点的堆栈来解决凸包问题。
操作:输入集合P中的每一个点都被压入栈一次,非凸包中的顶点的点最终将被弹出堆栈,
当算法终止时,堆栈中仅包含凸包中的顶点,其顺序为个各顶点在边界上出现的逆时针方向排列的顺序。
(1)设P0是P中Y坐标最小的点,如果有多个这样的点则取最左边的点作为P0;
(2) 设<P1,P2,……,Pn >是P中剩余的点,对其按逆时针方向相对P0 的极角进行排序,
如果有数个点有相同的极角,则去掉其余的点,只留下一个与P0 距离最远的那个点;
(3)
//前三个点先入栈
ch[0] = p[0];
ch[1] = p[1];
ch[2] = p[2];
//判断与其余所有点的关系
for (int i = 3; i < n; i++) {
//不满足向左转的关系,栈顶元素出栈
while (top > 0 && multiply(p[i], ch[top], ch[top - 1]) >= 0)
top--;
//当前点与栈内所有点满足向左关系,因此入栈.
ch[++top] = p[i];
}
原理:沿逆时针方向通过凸包时,在每个顶点处应该向左转。因此,while循环每次发现在一个顶点处没有向左转时,就把该顶点从堆栈中弹出。)当算法向点pi推进、在已经弹出所有非左转的顶点后,就把pi压入堆栈中。
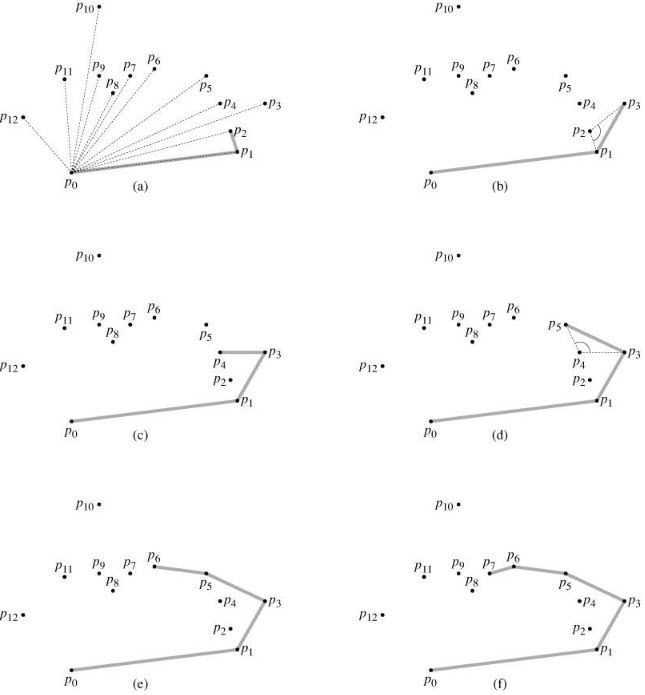
下面是POJ1113的AC代码:关于POJ1113请参见 http://128kj.iteye.com/blog/1748635
基本思想:通过设置一个关于候选点的堆栈来解决凸包问题。
操作:输入集合P中的每一个点都被压入栈一次,非凸包中的顶点的点最终将被弹出堆栈,
当算法终止时,堆栈中仅包含凸包中的顶点,其顺序为个各顶点在边界上出现的逆时针方向排列的顺序。
(1)设P0是P中Y坐标最小的点,如果有多个这样的点则取最左边的点作为P0;
(2) 设<P1,P2,……,Pn >是P中剩余的点,对其按逆时针方向相对P0 的极角进行排序,
如果有数个点有相同的极角,则去掉其余的点,只留下一个与P0 距离最远的那个点;
(3)
//前三个点先入栈
ch[0] = p[0];
ch[1] = p[1];
ch[2] = p[2];
//判断与其余所有点的关系
for (int i = 3; i < n; i++) {
//不满足向左转的关系,栈顶元素出栈
while (top > 0 && multiply(p[i], ch[top], ch[top - 1]) >= 0)
top--;
//当前点与栈内所有点满足向左关系,因此入栈.
ch[++top] = p[i];
}
原理:沿逆时针方向通过凸包时,在每个顶点处应该向左转。因此,while循环每次发现在一个顶点处没有向左转时,就把该顶点从堆栈中弹出。)当算法向点pi推进、在已经弹出所有非左转的顶点后,就把pi压入堆栈中。

下面是POJ1113的AC代码:关于POJ1113请参见 http://128kj.iteye.com/blog/1748635
import java.util.Scanner;
class Point {
double x;
double y;
public Point(int x, int y) {
this.x = x;
this.y = y;
}
}
public class Main {
Point[] ch; //点集p的凸包
Point[] p ; //给出的点集
int n;
int l;
int len=0;
public Main(Point[] p,int n,int l){
this.p=p;
this.n=n;
this.l=l;
ch= new Point[n];
}
//小于0,说明向量p0p1的极角大于p0p2的极角
public double multiply(Point p1, Point p2, Point p0) {
return ((p1.x - p0.x) * (p2.y - p0.y) - (p2.x - p0.x) * (p1.y - p0.y));
}
//求距离
public double distance(Point p1, Point p2) {
return (Math.sqrt((p1.x - p2.x) * (p1.x - p2.x) + (p1.y - p2.y)
* (p1.y - p2.y)));
}
public void answer(){
double sum = 0;
for (int i = 0; i < len - 1; i++) {
sum += distance(ch[i], ch[i + 1]);
}
if (len > 1) {
sum += distance(ch[len - 1], ch[0]);
}
sum += 2 * l * Math.PI;
System.out.println(Math.round(sum));
}
public int Graham_scan() {
int k = 0, top = 2;
Point tmp;
//找到最下且偏左的那个点
for (int i = 1; i < n; i++)
if ((p[i].y < p[k].y)
|| ((p[i].y == p[k].y) && (p[i].x < p[k].x)))
k = i;
//将这个点指定为pts[0],交换pts[0]与pts[k]
tmp = p[0];
p[0] = p[k];
p[k] = tmp;
//按极角从小到大,距离偏短进行排序
for (int i = 1; i < n - 1; i++) {
k = i;
for (int j = i + 1; j < n; j++)
if ((multiply(p[j], p[k], p[0]) > 0)
|| ((multiply(p[j], p[k], p[0]) == 0) && (distance(
p[0], p[j]) < distance(
p[0], p[k]))))
k = j; //k保存极角最小的那个点,或者相同距离原点最近
tmp = p[i];
p[i] = p[k];
p[k] = tmp;
}
//前三个点先入栈
ch[0] = p[0];
ch[1] = p[1];
ch[2] = p[2];
//判断与其余所有点的关系
for (int i = 3; i < n; i++) {
//不满足向左转的关系,栈顶元素出栈
while (top > 0 && multiply(p[i], ch[top], ch[top - 1]) >= 0)
top--;
//当前点与栈内所有点满足向左关系,因此入栈.
ch[++top] = p[i];
}
len=top+1;
return len;
}
public static void main(String[] args) {
Scanner in=new Scanner(System.in);
int n = in.nextInt();
int l = in.nextInt();
int x, y;
Point[] p = new Point[n];
for (int i = 0; i < n; i++) {
x = in.nextInt();
y = in.nextInt();
p[i] = new Point(x, y);
}
Main ma=new Main(p,n,l);
ma.Graham_scan();
ma.answer();
}
}