深入分析各排序算法
排序是一个非常常见的问题:
排序分为内部排序和外部排序;内部排序:内部排序是指待排序列完全存放在内存中所进行的排序过程,适合不太大的元素序列。
排序算法算是认识算法的一个基础,七种排序算法:冒泡排序,选择排序,快速排序,堆排序,shell排序,基数排序,归并排序。
时间复杂度与空间复杂度:
排序算法的效率是一个大问题,然而衡量效率的最好办法之一就是通过计算各排序算法的时间复杂度和空间复杂度,空间复杂度是相对来说比较好分析的,时间复杂度就相对比较难。
首先我们先看看各个排序的时间复杂度:
| 排序法 |
最差时间分析 |
平均时间复杂度 |
稳定度 |
空间复杂度 |
| 冒泡排序 |
O(n2) |
O(n2) |
稳定 |
O(1) |
| 快速排序 |
O(n2) |
O(n*log2n) |
不稳定 |
O(log2n)~O(n) |
| 选择排序 |
O(n2) |
O(n2) |
稳定 |
O(1) |
| 二叉树排序 |
O(n2) |
O(n*log2n) |
不一顶 |
O(n) |
| 插入排序 |
O(n2) |
O(n2) |
稳定 |
O(1) |
| 堆排序 |
O(n*log2n) |
O(n*log2n) |
不稳定 |
O(1) |
| 希尔排序 |
O |
O |
不稳定 |
O(1) |
| 桶排序 |
O(n) |
O(n) |
稳定 |
O |
| 归并排序 |
O(nlogn) |
O(nlogn) |
稳定 |
O(n) |
(本表格来自互联网http://blog.csdn.net/wuxinyicomeon/article/details/5996675)
排序算法的时间复杂度主要是看比较次数,比较次数多的时间复杂度高,以上时间复杂度的计算只是一个粗略的估计值,真正要计算一个排序法的时间效率需要实际运行,但是由于这样代价太大,也没有必要,所以采用的时间复杂度来表示。
对于冒泡排序,选择排序来说,它们比起其他算法就弱势很多,因为他们的时间复杂度最差和平均情况都要比其他算法要差,shell排序是选择排序的变种,然而它却很不稳定,这里附上探讨shel排序的连接(http://blog.csdn.net/gulianchao/article/details/8581210),有兴趣的同学可以看看:然而快速排序、二叉树排序、堆排序,归并排序和桶排序却各有千秋。
在实际工程上,我们都如何去选择排序方法呢?
研究这个问题我们首先要明白各个算法为什么快:
快速排序之所比较快,因为相比冒泡排序,每次交换是跳跃式的。每次排序的时候设置一个基准点,将小于等于基准点的数全部放到基准点的左边,将大于等于基准点的数全部放到基准点的右边。这样在每次交换的时候就不会像冒泡排序一样每次只能在相邻的数之间进行交换,交换的距离就大的多了。因此总的比较和交换次数就少了,速度自然就提高了。当然在最坏的情况下,仍可能是相邻的两个数进行了交换。因此快速排序的最差时间复杂度和冒泡排序是一样的都是O(N2),它的平均时间复杂度为O(NlogN)。其实快速排序是基于一种叫做“二分”的思想。我们后面还会遇到“二分”思想,到时候再聊。
摘自:(http://developer.51cto.com/art/201403/430986.htm)
交换的跳跃式,二分是快排胜出的关键,同样的思想也用在了shell排序上,shell排序的交换比较也是跳跃性的,所以在某些场合下,shell排序往往表现很好。
然而我们也应该注意到,快排也会存在一定的小概率事件产生平方级的时间复杂度。所以在要求一定不能产生平方级时间复杂度的情况下,快排是不适宜的。
接下来是堆排序:
参考文献:http://www.cnblogs.com/dolphin0520/archive/2011/10/06/2199741.html
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
我们将看到,堆结构上的一些基本操作的运行时间至多是与树的高度成正比,为O(lgn)。
至于,快速排序和堆排序哪个比较快。我看了很多资料,也有人在网上做了实验,但是看了他们的评论我有点迷茫了……
有人挺堆排序,认为数据量大的时候,堆排序的效率更高:
http://www.cnblogs.com/bamboo-talking/archive/2011/02/20/1959224.html
也有人挺快排的;
看了很多好的资料,有一篇也是写得比较好的,其中提到一个很关键的点“普通快排较之堆排没有优势,但是如果对快排进行优化就是另一种情况”
http://blog.csdn.net/bingjing12345/article/details/7827419
同时我本身也做了一个实验,产生10000个随机数,使用各种排列方式进行
从实验结果我们可以看出,插入排序保持着倒数第一的“领先位置”,shell排序是插入排序的变种,当然从此次试验结果来看,shell排序的优势并不明显,进一步说明了shell排序是一种不稳定的排序方式。快速排序,归并排序,基数排序在0.001秒级,而堆排序和分配排序在0.01秒级。篇幅有限,这里不叙述更多结果,有兴趣的朋友可以自行实验。(我已经附上我几次的实验结果和排序源代码)
根据收集到的数据资料,我们可以得出以下结论:
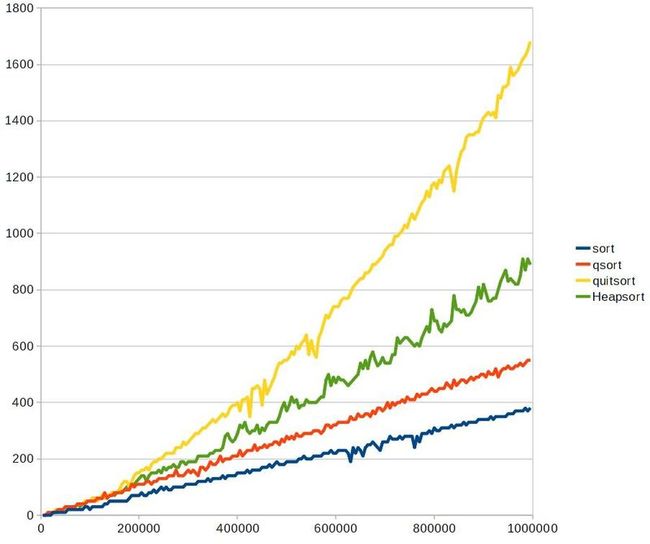
对于普通快排,优化快排,堆排的效率比较从低到高排列的顺序为:
普通快排<堆排<优化快排
图表可证:http://hi.baidu.com/ycdoit/item/6b5f5b9571a843becc80e560
黄色的曲线为优化后的快排,优势非常明显地体现出来了,然而我们怎么去优化他们呢:
各种各样的快排优化:
1) 利用存储子任务的栈来消除递归(递归里面,函数调用的轨迹都是放在栈上,若递归层次太多的话,很有可能栈还会溢出,一般系统都限制了栈的大小。并且压入弹出、恢复现场一大堆的,太麻烦了。)
2) 利用基于三中值分区的中枢值
3) 设定一个使用切分时数组长度的最小值,如果小于这个值,就使用插入排序(这个最小值根据经验给定,一般设定为4)
4) 当处理子数组的时候,首先将大的子数组压入栈中,这样可以最小化栈的总大小,确保小的问题首先被解决
Sedgewick(1978) 建议在快速排序中结合三中值和在排序小数组时使用插入排序这两种手段,这样能够相比纯快排提高20%-25%的性能。
所以为何我们在实际中用得最多的是快排。
接下来讨论的是归并排序与快排的比较:
<!--[if !supportLists]-->1.<!--[endif]--> 快排的时间复杂度是不稳定的,在最快情况下比归并排序慢的多。
2. 当数据量大时,充分优化的归并排序可比快速排序更快。其原因有
1). 归并排序对内存的访问是严格的顺序方式(3个2个源数组,1个目标数组,都是顺序放分),故cache的命中率比快排更高,从这点上,相同的内存读写操作,归并优于快排,当数组占用的空间大大超过cache的大小,则这一优势将更加明显。
2)1.普通写法的归并排序有2个缺点,如果改进,则可以提速。如果你的实验是基于最普通的版本,得到的结果是快排优于归并,而优化的归并排序的版本,其性能则可能反超快排。
2.1) 归并排序不是In place.需要将结果存储到临时缓冲区,然后在复制回来,这个过程可以优化掉。使用乒乓做法,在第i级归并过程,从buff1 归并到buff2,在i+1级归并过程,从buff2复制到buff1。
2.2) 2路归并排序的核心动作是比较2个对列的头元素那个更大,其比较结果是随机的,2个分支机会均等,CPU的分支预测算法不起作用,当预测失败,可大大降低程序性能,如果消除这个分支,可明显提高程序性能。
http://bbs.csdn.net/topics/390554511
这段介绍也是有离有据,令人信服,简单地说,这段话指出了归并排序较之快排的两大优势:cache的命中率高,稳定
所以归并也是排序算法中一个不错的选择;
而基数排序又如何呢:
分配排序、桶排序、基数排序是一脉相承的,他们都不是基于比较而是基于分配,所以他们的效率是非常高的。
介绍一篇比较好的博文:http://blog.csdn.net/quietwave/article/details/8008572
这篇博文分析得很透彻,这里就不再重复叙述
虽然说排序是最基本的问题之一,但如果你细心深挖,仍然有很多值得研究的问题,技术的提升首先是从理论到实践,而更进一步的是从实践中寻找问题深挖。
本文从时间效率入手,深入分析了如何去选择排序算法。也借鉴了很多资料,再次鸣谢各位对我的帮助,同时也把自己学到的东西整理出来分享给大家。希望大家共同提高。
最后附上实现的代码已经几次数据测试结果。