POJ 3253--Fence Repair
在写这道题之前,先介绍几点知识。
一、 动态规划(DP)
动态规划(dynamic programming)是求解决策过程最优化的数学方法。早在20世纪50年代初美国数学家R.E.Bellman等人就提出了著名的最优化原理,把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
DP是对解最优化问题的一种途径、一种方法,而不是一种特殊算法。由于各种问题的性质不同,确定最优解的条件也互不相同,因为动态规划的设计方法对不同的问题,除了要对基本概念和方法正确理解外,必须具体问题具体分析处理,以丰富的想象力去建立模型,用创造性的技巧去求解。按道理来说,计算机科学的更新速度是很快的,但现在所学的好多算法都是50年代、70年代的,可见此算法的精髓所在,同时也鼓励大家有自己的想法。
二、 堆
堆有最大堆和最小堆之分,最大堆就是每个节点的值都>=其左右孩子(如果有的话)值的 完全二叉树。最小堆便是每个节点的值都<=其左右孩子值的 完全二叉树。
堆的三种基本操作:
⑴最大堆的插入
由于需要维持完全二叉树的形态,需要先将要插入的结点x放在最底层的最右边,插入后满
足完全二叉树的特点;
然后把x依次向上调整到合适位置满足堆的性质
时间:O(logn)。
“结点上浮”

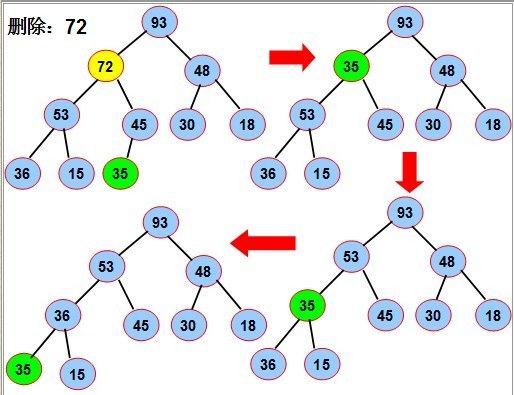
⑵删除
要从大小为n的堆中删除结点a[i]:
用a[n]来替换a[i];
堆的大小减1(dec(n));
把a[i](原a[n])下调到合适位置。//往上已符合堆?
“结点下沉”
⑶初始化
方法1:插入法:
从空堆开始,依次插入每一个结点,直到所有的结点全部插入到堆为止。
时间:O(n*log(n))
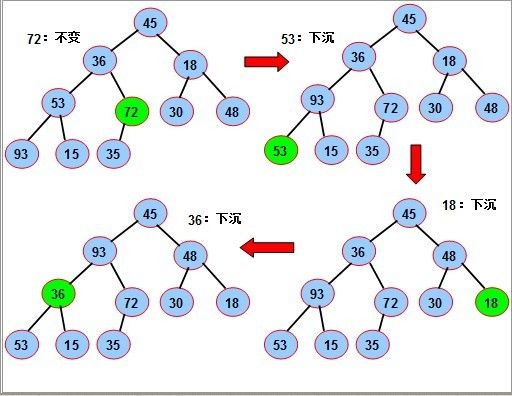
方法2:调整法:
序列对应一个完全二叉树;从最后一个分支结点(n div 2)开始,到根(1)为止,依次
对每个分支结点进行调整(下沉),以便形成以每个分支结点为根的堆,当最后对树根结点
进行调整后,整个树就变成了一个堆。
时间:O(n)


三、 哈夫曼树(堆的应用之一)
现在才切到正题,哈夫曼树便是由最小堆来建立的,最小堆中的每一个元素包括一棵二叉树及其权重值。
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree),当然它满足堆的性质。
先了解几个基本术语:
⑴ 路径和路径长度
在一棵树下,从一个结点往下可以达到的孩子或子孙节点之间的通路,称为路径。通路中分
支的数目称为路径长度。若规定根节点的层数为1,则从根节点到第L层的路径长度为L-1
⑵ 结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径
长度为:从根节点到该结点之间的路径长度与该结点的权的乘积
⑶ 树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL= Σ (wi x li),其中wi是叶子结点的权重,li是从根到该叶子结点的路径长度, 注意,带全路径长度只有叶子结点有权重,其他结点只计算长度无权重!
首先先来看看为什么哈夫曼树是最优的二叉树

WPL(a) = 7*2 + 5* 2 + 2*2 +4*2 = 36
WPL(b)=4*2 + 7*3 + 5*3 + 2 = 46
WPL(c) = 7 + 5 * 2 + 3 * 2 + 4 * 3 = 35
所以c是最优二叉树。
POJ 3253这道题的大意是有一个农夫要把一个木板砍成几块给定长度的小木板,每次据都要收取一定费用,这个费用就是据的这个木版的长度,用赫夫曼树的思路,用优先队列实现。逆向思维,每次都把木板拼接,要想每次都花费最少就得取最小的两个木板拼接起来再把拼接好的木板入队。
java 代码:
一、 动态规划(DP)
动态规划(dynamic programming)是求解决策过程最优化的数学方法。早在20世纪50年代初美国数学家R.E.Bellman等人就提出了著名的最优化原理,把多阶段过程转化为一系列单阶段问题,利用各阶段之间的关系,逐个求解,创立了解决这类过程优化问题的新方法——动态规划。
虽然动态规划主要用于求解以时间划分阶段的动态过程的优化问题,但一些与时间无关的静态规划(如线性规划、非线性规划),只要人为地引进时间因素,把它视为多阶段决策过程,也可以用动态规划方法方便地求解。
DP是对解最优化问题的一种途径、一种方法,而不是一种特殊算法。由于各种问题的性质不同,确定最优解的条件也互不相同,因为动态规划的设计方法对不同的问题,除了要对基本概念和方法正确理解外,必须具体问题具体分析处理,以丰富的想象力去建立模型,用创造性的技巧去求解。按道理来说,计算机科学的更新速度是很快的,但现在所学的好多算法都是50年代、70年代的,可见此算法的精髓所在,同时也鼓励大家有自己的想法。
二、 堆
堆有最大堆和最小堆之分,最大堆就是每个节点的值都>=其左右孩子(如果有的话)值的 完全二叉树。最小堆便是每个节点的值都<=其左右孩子值的 完全二叉树。
堆的三种基本操作:
⑴最大堆的插入
由于需要维持完全二叉树的形态,需要先将要插入的结点x放在最底层的最右边,插入后满
足完全二叉树的特点;
然后把x依次向上调整到合适位置满足堆的性质
时间:O(logn)。
“结点上浮”

⑵删除
要从大小为n的堆中删除结点a[i]:
用a[n]来替换a[i];
堆的大小减1(dec(n));
把a[i](原a[n])下调到合适位置。//往上已符合堆?
“结点下沉”

⑶初始化
方法1:插入法:
从空堆开始,依次插入每一个结点,直到所有的结点全部插入到堆为止。
时间:O(n*log(n))
方法2:调整法:
序列对应一个完全二叉树;从最后一个分支结点(n div 2)开始,到根(1)为止,依次
对每个分支结点进行调整(下沉),以便形成以每个分支结点为根的堆,当最后对树根结点
进行调整后,整个树就变成了一个堆。
时间:O(n)



三、 哈夫曼树(堆的应用之一)
现在才切到正题,哈夫曼树便是由最小堆来建立的,最小堆中的每一个元素包括一棵二叉树及其权重值。
给定n个权值作为n个叶子结点,构造一棵二叉树,若带权路径长度达到最小,称这样的二叉树为最优二叉树,也称为哈夫曼树(Huffman tree),当然它满足堆的性质。
先了解几个基本术语:
⑴ 路径和路径长度
在一棵树下,从一个结点往下可以达到的孩子或子孙节点之间的通路,称为路径。通路中分
支的数目称为路径长度。若规定根节点的层数为1,则从根节点到第L层的路径长度为L-1
⑵ 结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径
长度为:从根节点到该结点之间的路径长度与该结点的权的乘积
⑶ 树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL= Σ (wi x li),其中wi是叶子结点的权重,li是从根到该叶子结点的路径长度, 注意,带全路径长度只有叶子结点有权重,其他结点只计算长度无权重!
首先先来看看为什么哈夫曼树是最优的二叉树

WPL(a) = 7*2 + 5* 2 + 2*2 +4*2 = 36
WPL(b)=4*2 + 7*3 + 5*3 + 2 = 46
WPL(c) = 7 + 5 * 2 + 3 * 2 + 4 * 3 = 35
所以c是最优二叉树。
POJ 3253这道题的大意是有一个农夫要把一个木板砍成几块给定长度的小木板,每次据都要收取一定费用,这个费用就是据的这个木版的长度,用赫夫曼树的思路,用优先队列实现。逆向思维,每次都把木板拼接,要想每次都花费最少就得取最小的两个木板拼接起来再把拼接好的木板入队。
java 代码:
import java.util.PriorityQueue;
import java.util.Scanner;
public class Main {
PriorityQueue<Long> qq = new PriorityQueue<Long>(20000);
void run() {
Scanner scan = new Scanner(System.in);
long sum = 0, x, y, temp;
int n = scan.nextInt();
for (int i = 0; i < n; i++)
qq.add(scan.nextLong());
for (int i = 1; i < n; i++) {
x = qq.poll();
y = qq.poll();
temp = x + y;
sum += temp;
qq.add(temp);
}
System.out.println(sum);
}
public static void main(String[] args) {
new Main().run();
}
}