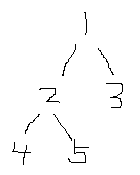之前小试的看过一些关于最近公共祖先LCA的离线算法,个人感觉很多博文说的还是不够清晰,一直没搞太懂,不知道是不是最近智商退化导致的,今天花时间细致了解了Tarjan,这篇文章主要说下算法和树结构最近公共祖先的计算,另外一些扩展应用在后续的帖子再说。
下面这篇博客中的伪码对我帮助很大,希望也能对不太明白的童鞋有帮助,后面还会提到。
http://blog.csdn.net/cxllyg/article/details/7635992
这里默认了解了并查集,并查集还是比较简单,很多的博客也都说的非常清楚,具体的一个非常生动的例子:http://blog.csdn.net/ljfbest/article/details/6642769
这里给出一个基本实现的代码版本:
public class DisjointSet<T> {
public static class Node<T>{
T data; //Node的数据
int rank = 0; //祖先节点的rank,rank小的节点表示孩子少,合并的时候加入到rank大的树下
Node<T> father; //父节点/祖先节点
public Node(T data){
this.data = data;
this.father = this;
this.rank = 0;
}
}
/**
* 找到祖先节点
* @param x
* @return
*/
public Node<T> find(Node<T> x){
//当自己是祖先的时候直接返回
if (x == x.father){
return x;
}
//当自己的父节点不是祖先的时候,压缩树直接连接到祖先节点
x.father = find(x.father);
return x.father;
}
/**
* x和y节点之间有连接,将其所属集合连接。rank值小的树加到rank值大的树下面。相同时y加到x下。
* @param x
* @param y
*/
public void Union(Node<T> x, Node<T> y){
Node<T> xFather = find(x);
Node<T> yFather = find(y);
//当两个结合不联通的时候根据rank值,将rank值小的树加到rank值大的树下面
if(xFather==yFather){
return;
}else if(xFather.rank >yFather.rank)
yFather.father = xFather;
else if(xFather.rank < yFather.rank)
xFather.father = yFather;
else{
yFather.father = xFather;
xFather.rank++;
}
}
}
进入正题看Tarjan,LCA最本质的应用就是查找两个节点最近的公共节点。比如
伪码直接摘用的博客上的,主要在后面做一些补充。
LCA(u){
Make-Set(u)
ancestor[Find-Set(u)]=u
对于u的每一个孩子v{
LCA(v)
Union(u)
ancestor[Find-Set(u)]=u
}
checked[u]=true
对于每个(u,v)属于P{
if checked[v]=true
then {
回答u和v的最近公共祖先为 ancestor[Find-Set(v)]
}
}
}
其中,makest就是建立一个集合,makeset(u )就是建立一个只含U的集合。
findset(u)是求跟U一个集合的一个代表,一般此集合用并查集表示,也就是当前树的root节点。
union()就是把 V节点生成的子树并入U中。
ancestor就是找跟节点,一直往上找,直至某节点的父节点是自己为止。
对于上面显示的并查集的基本demo而言,MakeSet和ancestor操作都不需要做,因此稍微简化一下,给出段代码,重要是关注这个流程,以上面的例子来说明。
LCA(u) {
对于u的每一个孩子v {
LCA(v)
Union(u,v)
}
checked[u]=true
对于每个(u,v)属于P {
if checked[v]=true then 回答u和v的最近公共祖先为 ancestor[Find-Set(v)]
}
}
1. 首先考虑下用并查集,很容易做最远公共祖先(当然,树的时候就是根),然后按这个思路需要做的就是怎么找到4、5的公共节点是2
2. 开始写了很多,但觉着这个伪码就比较清楚了,就简单说一下关键。这里可以看到是深度优先的计算,并且每个子集都优先计算子树,之后把全部的父节点都指向集合的父节点,这样的作用是比如一个二叉树,左子树单独进行处理,使得两点都在左子树上的节点的最近公共节点是左子树的根节点,当处理完后和根节点组合,进入右节点的时候,可以看到所有的节点和左子树的最近公共节点就是根节点,但是右子树内部的都单独在一个集合中,另外更右的子树没有处理过,不进行计算。按照这个方式,不断的这样处理,就通过递归从左向右不断处理,完成整个过程。
3. 还有需要注意的一点就是(u,v)这个顺序很重要,因此每个uv的组合需要先做两次的存储,实际uv和vu只会处理一个
因为伪码比较清楚了,搜了很多帖子,看到这段伪码想想就大概清楚了,这里就贴上代码,很多算法大牛们的代码都太不易懂了,我还是来点工程版的
/**
* 对于树结构的LCA_Tarjan
*
* @author Jason_wbw
*
*/
public class LCA_Tarjan<T> {
public static class Node<T>{
T data; //Node的数据
Node<T> father; //父节点/祖先节点
List<Node<T>> children;
public Node(){}
public Node(T data){
this.data = data;
this.father = this;
children = new ArrayList<Node<T>>();
}
}
public static class Pair<T>{
Node<T> p, q;
Node<T> lca;
public Pair(Node<T> p, Node<T> q){
this.p = p;
this.q = q;
}
}
List<Pair<T>> list; //结果
Map<Node<T>,List<Node<T>>> pairs; //对应于(u,v),对于一个元组需要存储uv和vu
Map<Node<T>,Boolean> checked; //对应于checked[]
public List<Pair<T>> getLCA(Node<T> root, List<Pair<T>> list){
checked = new HashMap<Node<T>,Boolean>();
this.list = new LinkedList<Pair<T>>();
//构建所有需要查询的元组
pairs = new HashMap<Node<T>,List<Node<T>>>();
for(Pair<T> p : list){
if(pairs.get(p.p)==null)
pairs.put(p.p, new LinkedList<Node<T>>());
pairs.get(p.p).add(p.q);
if(pairs.get(p.q)==null)
pairs.put(p.q, new LinkedList<Node<T>>());
pairs.get(p.q).add(p.p);
}
//进入实际算法
LCA(root);
return this.list;
}
private void LCA(Node<T> u){
//完全依照伪码部分实现
for(Node<T> v:u.children){
LCA(v);
union(u, v);
}
checked.put(u, true);
if(pairs.get(u)!=null){
for(Node<T> n : pairs.get(u)){
Boolean b = checked.get(n);
if(b!=null && b){
Pair<T> pair = new Pair<T>(u,n);
pair.lca = find(n);
list.add(pair);
}
}
}
}
//--------------------------------------------------------------------
//并查集操作
/**
* 找到祖先节点
* @param x
* @return
*/
public Node<T> find(Node<T> x){
//当自己是祖先的时候直接返回
if (x == x.father){
return x;
}
//当自己的父节点不是祖先的时候,压缩树直接连接到祖先节点
x.father = find(x.father);
return x.father;
}
/**
* x和y节点之间有连接,将其所属集合连接。rank值小的树加到rank值大的树下面。相同时y加到x下。
* @param x
* @param y
*/
public void union(Node<T> x, Node<T> y){
Node<T> xFather = find(x);
Node<T> yFather = find(y);
//当两个结合不联通的时候根据rank值,将rank值小的树加到rank值大的树下面
if(xFather==yFather){
return;
}else{
yFather.father = xFather;
}
}
}