Codeforces Beta Round #96 (Div. 2)【完整题解】
KIDx 的解题报告
题目链接:http://codeforces.com/contest/133
以下省略头文件,前三题是水题,不解释
A题
B题
C题
D题
表示偶的英语水平太特么烂,很久才看懂:
0-9表示颜色,输入一堆颜色像素
相同颜色所组成的一个长方形算一个块【看做整体】
初始时:
BP为左上角那整块的颜色,DP向右指到这整块的最远边,CP向上【DP的左方】指到这整块的远边
变换状态:
若DP所指的next为0或者空:【BP不变】
①若CP此时在DP左边,则DP不变,CP变成DP的右边,同时显然的CP会指到当前整块的CP方向最远处,此转换消耗一个步数
②若CP此时在DP右边,则DP顺时针转90°,CP变成DP的左边,同时DP与CP都会指到当前块各自方向的最远处,此转换消耗一个步数
若DP所指的next有颜色(1-9):
向DP方向走一步,同时DP指到该块DP方向的最远处,且BP变为该块的颜色,此转换消耗一个步数
然后还要找循环节,不然会超时:
定义一个hash[i][j][CP][DP]表示第一次走到i,j时方向为CP,DP这一状态的步数,设第二次再次获得此状态的步数为times,则循环时间loop = times - hash[i][j][CP][DP]
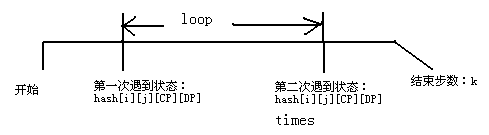
如图所示:
如果有循环节:
那么k必然>=times,观察可知:原来的模拟k次,其实相当于模拟:(times - loop + (k-times) % loop)次
E题
算法:DP
题意很简单:
F表示向前走,T表示转弯,给一个FT组成的串,F可以变T,T可以变F,一个字符可以变多次,问变n次后最多能走多远
状态的表示:
f[i][j][k]表示向前走的最长距离
g[i][j][k]表示向前走的最短距离【则(-g[i][j][k])表示向后走的最长距离】
i表示完成前i-1个字符命令
j表示完成前i-1个字符命令一共作了j次变换
k表示方向,k = 0 表示正在向前走,k = 1 表示正在向后走
题目链接:http://codeforces.com/contest/133
以下省略头文件,前三题是水题,不解释
A题
#define M 105
char s[M];
int main()
{
bool flag;
int i, len;
while (gets (s))
{
flag = false;
len = strlen (s);
for (i = 0; i < len; i++)
if (s[i] == 'H' || s[i] == 'Q' || s[i] == '9')
{
flag = true;
break;
}
if (flag)
puts ("YES");
else puts ("NO");
}
return 0;
}
B题
#define M 105
int mod = 1000003;
string s, b;
map<char, string> m;
int main()
{
int i, res, a;
m['>'] = "1000";
m['<'] = "1001";
m['+'] = "1010";
m['-'] = "1011";
m['.'] = "1100";
m[','] = "1101";
m['['] = "1110";
m[']'] = "1111";
while (cin >> s)
{
b = "";
for (i = 0; i < s.size(); i++)
b += m[s[i]];
res = 0, a = 1;
for (i = b.size() - 1; i >= 0; i--)
{
if (b[i] == '1')
res = (res + a) % mod;
a = (a << 1) % mod;
}
printf ("%d\n", res);
}
return 0;
}
C题
#define M 105
int mod = 256;
char s[M], p[M];
int main(
{
int i, k, pre, j;
while (gets (s))
{
pre = 0;
for (i = 0; i < strlen(s); i++)
{
int tp = int(s[i]);
k = 0;
while (tp) //讲tp转成2进制存到p
{
p[k++] = (tp % 2) + '0';
tp >>= 1;
}
while (k < 8) //补0
p[k++] = '0';
p[k] = 0;
for (j = 0; j < k; j++)
{
if (p[j] == '1')
tp += pow (2.0, k-j-1);
}
printf ("%d\n", ((pre-tp)%mod+mod)%mod); //将解限制到最小非负整数
pre = tp;
}
}
return 0;
}
D题
表示偶的英语水平太特么烂,很久才看懂:
0-9表示颜色,输入一堆颜色像素
相同颜色所组成的一个长方形算一个块【看做整体】
初始时:
BP为左上角那整块的颜色,DP向右指到这整块的最远边,CP向上【DP的左方】指到这整块的远边
变换状态:
若DP所指的next为0或者空:【BP不变】
①若CP此时在DP左边,则DP不变,CP变成DP的右边,同时显然的CP会指到当前整块的CP方向最远处,此转换消耗一个步数
②若CP此时在DP右边,则DP顺时针转90°,CP变成DP的左边,同时DP与CP都会指到当前块各自方向的最远处,此转换消耗一个步数
若DP所指的next有颜色(1-9):
向DP方向走一步,同时DP指到该块DP方向的最远处,且BP变为该块的颜色,此转换消耗一个步数
然后还要找循环节,不然会超时:
定义一个hash[i][j][CP][DP]表示第一次走到i,j时方向为CP,DP这一状态的步数,设第二次再次获得此状态的步数为times,则循环时间loop = times - hash[i][j][CP][DP]

如图所示:
如果有循环节:
那么k必然>=times,观察可知:原来的模拟k次,其实相当于模拟:(times - loop + (k-times) % loop)次
#define M 55
char map[M][M];
int x_move[4] = {-1, 0, 1, 0}; //四个方向:分别表示:上,右,下,左
int y_move[4] = {0, 1, 0, -1};
int hash[M][M][5][5];
int r, c, k, i, BP, CP, DP, bx, by, dir, tx, ty, loop, times;
void init () //设置初始状态
{
BP = map[0][0] - '0';
CP = -1;
DP = 1;
tx = ty = 0;
do{ //沿DP方向指到该块最远处
bx = tx, by = ty;
tx += x_move[DP];
ty += y_move[DP];
}while (!(tx < 0 || ty < 0 || tx >= r || ty >= c) &&
map[tx][ty] - '0' == BP);
times = 0;
}
void moni () //模拟
{
tx = bx + x_move[DP];
ty = by + y_move[DP];
if (tx < 0 || ty < 0 || tx >= r || ty >= c || map[tx][ty] == '0')
{
if (CP == 1)
DP = (DP + 1) % 4;
CP = -CP;
}
else
{
BP = map[tx][ty] - '0';
do{ //沿DP方向指到该块最远处
bx = tx, by = ty;
tx += x_move[DP];
ty += y_move[DP];
}while (!(tx < 0 || ty < 0 || tx >= r || ty >= c) &&
map[tx][ty] - '0' == BP);
}
dir = (DP+CP) % 4; //CP是-1时在DP左边,是1时在DP右边,dir为CP方向
tx = bx, ty = by;
do{ //沿CP方向指到该块最远处
bx = tx, by = ty;
tx += x_move[dir];
ty += y_move[dir];
}while (!(tx < 0 || ty < 0 || tx >= r || ty >= c) &&
map[tx][ty] - '0' == BP);
}
int main()
{
while (~scanf ("%d%d", &r, &k))
{
memset (hash, 0, sizeof(hash));
for (i = 0; i < r; i++)
scanf ("%s", map[i]);
c = strlen (map[0]);
init();
loop = 0;
while (times < k)
{
moni ();
if (hash[bx][by][CP+1][DP] > 0) //有重复状态,即找到循环节
{
loop = times - hash[bx][by][CP+1][DP];
break;
}
else hash[bx][by][CP+1][DP] = times;
times++;
}
if (loop > 0) //有循环节,重新模拟times-loop+(k-times)%loop次
{
k = times - loop + (k-times) % loop;
init();
while (k--) {moni ();}
}
printf ("%d\n", BP);
}
return 0;
}
E题
算法:DP
题意很简单:
F表示向前走,T表示转弯,给一个FT组成的串,F可以变T,T可以变F,一个字符可以变多次,问变n次后最多能走多远
状态的表示:
f[i][j][k]表示向前走的最长距离
g[i][j][k]表示向前走的最短距离【则(-g[i][j][k])表示向后走的最长距离】
i表示完成前i-1个字符命令
j表示完成前i-1个字符命令一共作了j次变换
k表示方向,k = 0 表示正在向前走,k = 1 表示正在向后走
#define inf 0x3fffffff
#define M 105
#define N 55
int f[M][N][2], g[M][N][2], d[2] = {1, -1}, tp, k2, i, j, k, num;
char s[M]; //d[1] = -1,说明向后走1步,也就是向前走-1步
void dp (int f[][N][2], int key)
{
tp = f[i][j][k], k2 = k;
if (num & 1) //变奇数次,s[i]肯定变成另一个字符
{
if (s[i] == 'T') tp += d[k]; //变成f,所以向前状态k方向走
else k2 = !k; //变成T,下一状态的方向k2变向
}
else //s[i]不变
{
if (s[i] == 'T') k2 = !k; //k2换向
else tp += d[k]; //向k方向走
}
if (key)
f[i+1][j+num][k2] = max (f[i+1][j+num][k2], tp);
else f[i+1][j+num][k2] = min (f[i+1][j+num][k2], tp);
}
int main()
{
int n, len;
while (~scanf ("%s", s))
{
len = strlen (s);
scanf ("%d", &n);
for (i = 0; i < M; i++)
for (j = 0; j < N; j++)
f[i][j][0] = f[i][j][1] = -inf,
g[i][j][0] = g[i][j][1] = inf;
f[0][0][0] = f[0][0][1] = g[0][0][0] = g[0][0][1] = 0;
for (i = 0; i < len; i++)
for (j = 0; j <= n; j++)
for (k = 0; k < 2; k++)
for (num = 0; j + num <= n; num++) //num表示让当前字符变多少次
{
if (f[i][j][k] > -inf) dp (f, 1); //对f进行dp
if (g[i][j][k] < inf) dp (g, 0); //对g进行dp
}
printf ("%d\n",
max (f[len][n][0],
max (f[len][n][1],
max (-g[len][n][0], -g[len][n][1]))));
}
return 0;
}