1. 2-3 tree
a) Allow 1 or 2 keys per node.
1) 2-node: one key, two children.
2) 3-node: two keys, three children.
b) Perfect balance: Every path from root to null link has same length.
c) Symmetric order: Inorder traversal yields keys in ascending order.
2. Search.
a) Compare search key against keys in node.
b) Find interval containing search key.
c) Follow associated link (recursively).
3. Insertion into a 3-node at bottom.
a) Add new key to 3-node to create temporary 4-node.
b) Move middle key in 4-node into parent.
c) Repeat up the tree, as necessary.
d) If you reach the root and it's a 4-node, split it into two 2-nodes.
Invariants: Maintains symmetric order and perfect balance.
4. Tree height.
a) Worst case: lg N. [all 2-nodes]
b) Best case: log3 N ≈ .631 lg N. [all 3-nodes]
c) Guaranteed logarithmic performance for search and insert.
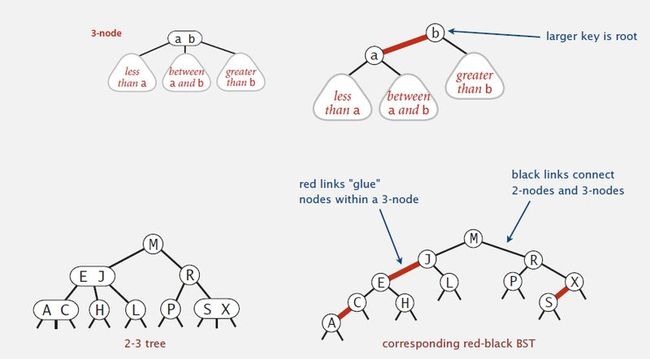
5. Left-leaning red-black BSTs
a) Represent 2–3 tree as a BST.
b) Use "internal" left-leaning links as "glue" for 3–nodes.
6. An equivalent definition :
A BST such that:
a) No node has two red links connected to it. ( no consecutive red nodes on any path)
b) Every path from root to null link has the same number of black links. ( same # of black nodes on any path)
c) Red links lean left.
7. Observations of Left-leaning red-black BSTs:
a) 1–1 correspondence between 2–3 and LLRB.
b) Search is the same as for elementary BST (ignore color).
c) Each node is pointed to by precisely one link (from its parent) ⇒ can encode color of links in nodes.
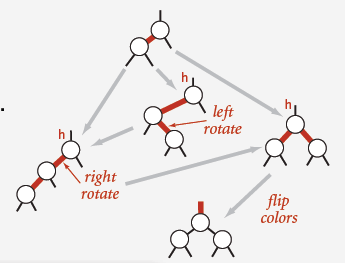
8. Elementary red-black BST operations
a) Left rotation: Orient a (temporarily) right-leaning red link to lean left:
private Node rotateLeft(Node h)
{
assert isRed(h.right);
Node x = h.right;
h.right = x.left;
x.left = h;
x.color = h.color;
h.color = RED;
return x;
}
b) Right rotation: Orient a left-leaning red link to (temporarily) lean right.
private Node rotateRight(Node h)
{
assert isRed(h.left);
Node x = h.left;
h.left = x.right;
x.right = h;
x.color = h.color;
h.color = RED;
return x;
}
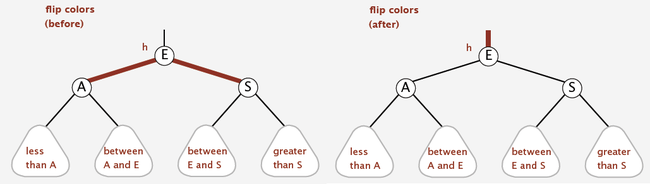
c) Color flip: Recolor to split a (temporary) 4-node.
private void flipColors(Node h)
{
assert !isRed(h);
assert isRed(h.left);
assert isRed(h.right);
h.color = RED;
h.left.color = BLACK;
h.right.color = BLACK;
}
8. Insertion in a LLRB tree:
a) Basic strategy. Maintain 1-1 correspondence with 2-3 trees by applying elementary red-black BST operations.
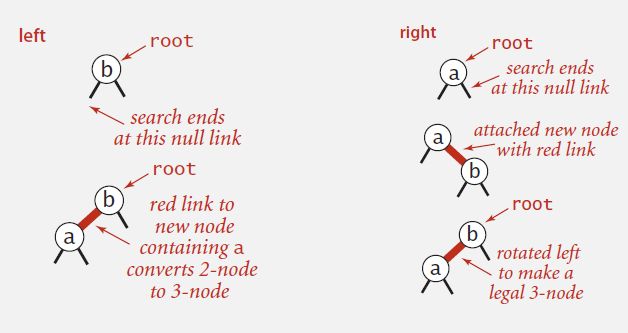
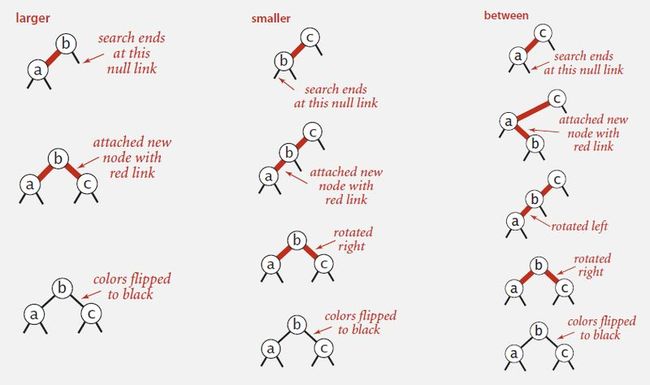
b) Case 1. Insert into a 2-node at the bottom.
1) Do standard BST insert; color new link red.
2) If new red link is a right link, rotate left.
c) Case 2. Insert into a 3-node at the bottom.
1) Do standard BST insert; color new link red.
2) Rotate to make lean left (if needed).
3) Rotate to balance the 4-node (if needed).
4) Flip colors to pass red link up one level.
5) Repeat case 1 or case 2 up the tree (if needed).
d) Same code for all cases.
1) Right child red, left child black: rotate left.
2) Left child, left-left grandchild red: rotate right.
3) Both children red: flip colors.
private Node put(Node h, Key key, Value val)
{
if (h == null) return new Node(key, val, RED);
int cmp = key.compareTo(h.key);
if (cmp < 0) h.left = put(h.left, key, val);
else if (cmp > 0) h.right = put(h.right, key, val);
else if (cmp == 0) h.val = val;
if (isRed(h.right) && !isRed(h.left)) h = rotateLeft(h);
if (isRed(h.left) && isRed(h.left.left)) h = rotateRight(h);
if (isRed(h.left) && isRed(h.right)) flipColors(h);
return h;
}
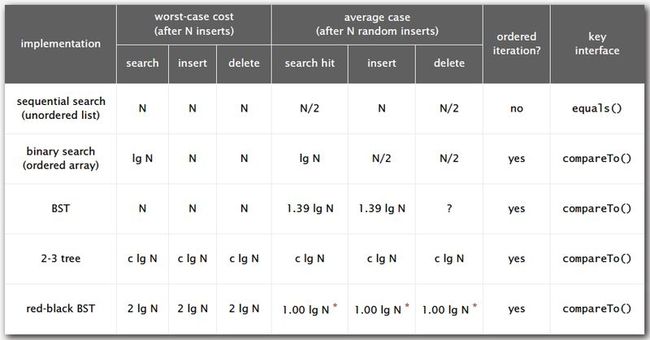
9. Symbol Table Implementation Summary :
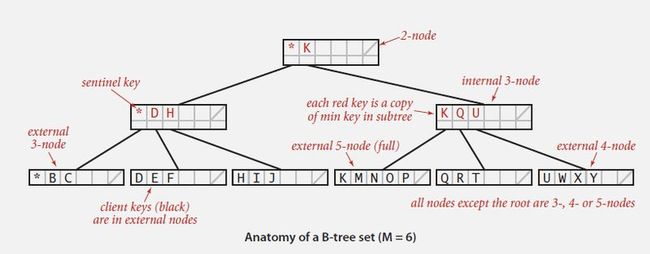
10. B-tree :
a) Generalize 2-3 trees by allowing up to M - 1 key-link pairs per node.
(choose M as large as possible so that M links fit in a page.)
b) At least 2 key-link pairs at root.
c) At least M / 2 key-link pairs in other nodes.
d) External nodes contain client keys.
e) Internal nodes contain copies of keys to guide search.
11. Search in a B-tree:
a) Start at root.
b) Find interval for search key and take corresponding link.
c) Search terminates in external node.
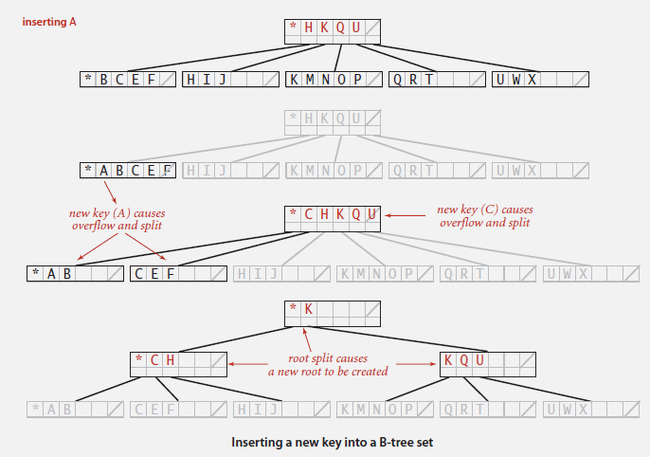
12. Insert in a B-tree:
a) Search for new key.
b) Insert at bottom.
c) Split nodes with M key-link pairs on the way up the tree.
13. Balance in B-tree:
a) A search or an insertion in a B-tree of order M with N keys requires between log M-1 ( N ) and log M/2 ( N ) probes. (Pf. All internal nodes except root have between M / 2 and M - 1 links.)
b) Optimization : Always keep root page in memory.