PKU 3675 Telescope .
Telescope
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 1178 | Accepted: 308 |
Description
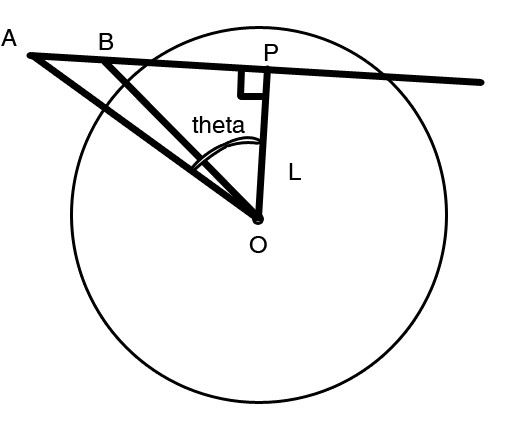
Updog is watching a plane object with a telescope. The field of vision in the telescope can be described as a circle. The center is at the origin and the radius is R. The object can be seen as a simple polygon of N vertexes. Updog wants to know the area of the part of the object that can be seen in the telescope.
Input
The input will contain several test cases. For each case:
The first line contains only one real number R.
The second line contains an integer N. The following N lines contain two real numbers xi and yi each, which describe the coordinates of a vertex. Two vertexes in adjacent lines are also adjacent on the polygon.
Constraints: 3 ≤ N ≤50, 0.1 ≤ R ≤1000, -1000 ≤ xi, yi ≤ 1000
Output
For each test case, output one real number on a separate line, which is the area of the part that can be seen. The result should be rounded to two decimal places.
Sample Input
10 3 0 20 10 0 -10 0
Sample Output
144.35
Source
尼条题真系做死窝，同FFT有得比。
题目大意就系求一个以源点为圆心既圆同埋另一个简单多边形既交积。
用非常麻烦但系又非常重要既三角剖分。
算法思路其实好简单，就系以输入点顺序依次扫描每一对相邻点，求出以圆心，多边形相邻两点与圆既相交“向量面积”(就系有方向既面积)。
将所有向量积相加后再取绝对值就系最终结果。
要分类讨论所有相交情况，再将解法类似既分为一类，所以我总共分左11小类同三大类
首先如图做一滴假设：
假设始终有OA ≥OB，有呢个假设就可以省略某些可能鸟，圆半径为R。
：
第一大类：
OA >R 且 OB>R
有四小类:
第二大类:
OA > R 且 OB ≤ R
都系有四小类:
第三大类:
OA ≤ R 且 OB ≤ R
有三个小类:
如果按照解答方法黎分，就系呢三大类。
跟住讲解法：
第一大类里面123小类直接求出扇形面积即可，4小类需要减去两条蓝边端点与弧形成既弓型，即减去一扇形再加上一个三角形。
第二大类里面123小类要将相交面积用蓝线分成两部分分别求解，呢度要得出小扇形既角度可以通过求出蓝线向量用点积求得，三
角形面积都可以用蓝线向量用叉积求得，4小类直接求扇形面积即可。
第三大类最爽，直接用OA，OB求叉积即刻得出向量积。
下面有三个比较重要既点:
一、蓝线向量OK可以通过以下向量运算求出：
OK = OP + PK
PK = |PK|/|BA| * BA (因为|PK|同埋|BA|共线同向，所以|PK|可以通过改变|AB|长度得到)
|PK|^2 = R^2 + |OP|^2
二、P点可以用向量点积运算加解释几何方法求出：
因为OP * AB = 0(垂直) 所以OP = (-Yab, Xab)
跟住用一般式Ax + By + C = 0分求出P点，用一般式系避免斜率分类。
三、我WA既罪人。
注意第一大类第四小类判断方法要加上判断P点系唔系线段AB上，呢个系区分12同埋34类既关键
不过123类同一解法，所以其实就系4小类要加上。
下面贴上代码:
| 8994621 | GZHU1006100106 | 3675 | Accepted | 224K | 0MS | C++ | 2887B | 2011-07-25 15:52:39 |
#include <iostream>
#include <cmath>
using namespace std;
#define MAXI 0x400
#define sq(x) ((x) * (x))
#define sng(x) (x == 0.0? 0.0: (x > 0? 1.0: -1.0))
#define fmax(x, y) (x > y? x: y)
#define fmin(x, y) (x < y? x: y)
struct pt
{
double x, y;
pt(double a = 0, double b = 0)
{
x = a;
y = b;
}
double len() { return sqrt(sq(x) + sq(y)); }
double operator * (pt o) { return x * o.y - o.x * y; }
double operator % (pt o) { return x * o.x + y * o.y; }
} ps[MAXI];
struct sg
{
pt a, b;
double A, B, C;
sg(pt x, pt y)
{
a = x;
b = y;
A = a.y - b.y;
B = b.x - a.x;
C = -(a.y * B + a.x * A);
}
bool ons(pt o)
{
if (fmin(a.x, b.x) <= o.x && o.x <= fmax(a.x, b.x))
if (fmin(a.y, b.y) <= o.y && o.y <= fmax(a.y, b.y))
return 1;
return 0;
}
double len() { return sqrt(sq(a.x - b.x) + sq(a.y - b.y)); }
double ang() { return acos((a % b) / (a.len() * b.len())); }
pt inr(sg o)
{
double d = (A * o.B - o.A * B);
double x = B * o.C - o.B * C;
double y = A * o.C - o.A * C;
return pt(x / d, -y / d);
}
};
double r;
int n;
double TGL(pt a, pt b) //Triangulate
{
#if 0
printf("a = [%.2lf, %.2lf], b = [%.2lf, %.2lf]\n", a.x, a.y, b.x, b.y);
putchar('\n');
#endif
double sn = sng(a * b);
if (a.len() < b.len())
swap(a ,b);
pt lp(a.x - b.x, a.y - b.y), np(-lp.y, lp.x), cp;
sg l(a, b), nl(pt(0, 0), np);
pt tp = l.inr(nl);
double tsu = 0;
double oa = a.len();
double ob = b.len();
double ol = tp.len();;
double ang, d;
if (oa == 0.0 || oa == 0.0 || ol == 0.0)
return 0.0;
if (oa <= r && ob <= r)
{
tsu += fabs(a * b / 2.0);
#if 0
printf("stu 1");
putchar('\n');
#endif
}
else if (oa > r && ob <= r)
{
d = sqrt(sq(r) - sq(tp.len())) / l.len();
tp = pt(tp.x + lp.x * d, tp.y + lp.y * d);
ang = sg(a, tp).ang();
tsu += ang * sq(r) / 2.0;
tsu += fabs(tp * b/ 2.0);
#if 0
printf("stu 2");
printf("tp = [%.2lf, %.2lf]\n", tp.x, tp.y);
printf("part1 : %.2lf part2 %.2lf\n", ang * sq(r) / 2.0, fabs(tp * b/ 2.0));
putchar('\n');
#endif
}
else
{
ang = acos(ol / r);
tsu += l.ang() * sq(r) / 2.0;
if (oa > r && ob > r && ol < r && l.ons(tp))
tsu += ol * r * sin(ang) - ang * sq(r);
#if 0
printf("stu 3\n");
printf("%.2lf\n", acos(ol / r));
printf("part1 : %.2lf part2 %.2lf\n", l.ang() * sq(r) / 2.0, ol * r * sin(ang) - ang * sq(r));
putchar('\n');
#endif
}
#if 0
printf("tsu = %.2lf\n\n", tsu * sn);
#endif
return tsu * sn;
}
int main()
{
int i;
double tsu;
while (scanf("%lf", &r) != EOF)
{
scanf("%d", &n);
for (i = 0; i < n; i++)
scanf("%lf%lf", &ps[i].x, &ps[i].y);
tsu = 0.0;
for (i = 0; i < n; i++)
tsu += TGL(ps[i], ps[(i + 1) % n]);
printf("%.2lf\n", fabs(tsu));
}
return 0;
}
如果大家吾爽滴宏逻辑开关可以删左再睇代码，你会发觉短左好多{= __.=}。
今次系我第一次用埋PS写BLOG，图文结合应该好理解吧。
