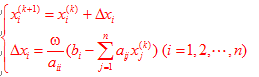作为迭代法一种加速方法,超松弛迭代法计算公式简单,只是需要选择合适的松弛因子,保证迭代过程有较快的收敛速度。它是Gauss-Seidel迭代法的优化。而列主元消去法,因为仅按列选主元,相比完全主元消元法,省了主元搜寻时间,提高了效率。
SOR迭代公式:
SOR编程代码如下:
函数:
function [xvect,nvect,xdif]=SOR(A,b,eps,x0,w) %超松弛迭代法
m=length(b); %m为线性方程组的维数,即变量的个数
xvect=[]; %为length(b)行length(nvect)列的矩阵,存储X1~X(length(b))变量的迭代值
nvect=[]; %存贮迭代次数
xdif=[]; %存储误差 max(1<=i<=length(b))abs(xi(k+1)-xi(k))
n=1; xvect=[xvect;x0];
x1=[];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%计算由初值x0经第一次迭代后的值x1
x1(1)=x0(1)+w/A(1,1)*(b(1)-sum(A(1,[1:m]).*x0([1:m])));
for i=2:m-1
x1(i)=x0(i)+w/A(i,i)*(b(i)-sum(A(i,[1:i-1]).*x1([1:i-1]))-sum(A(i,[i:m]).*x0([i:m])));
end
x1(m)=x0(m)+w/A(m,m)*(b(m)-sum(A(m,[1:m-1]).*x1([1:m-1]))-A(m,m)*x0(m));
xvect=[xvect;x1];nvect=[nvect;n];err=max(abs(x0-x1));xdif=[xdif;err];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%下面是迭代过程
while(err>eps)
x2=x1;
x1(1)=x1(1)+w/A(1,1)*(b(1)-sum(A(1,[1:m]).*x1([1:m])));
for i=2:m-1
x1(i)=x1(i)+w/A(i,i)*(b(i)-sum(A(i,[1:i-1]).*x1([1:i-1]))-sum(A(i,[i:m]).*x1([i:m])));
end
x1(m)=x1(m)+w/A(m,m)*(b(m)-sum(A(m,[1:m]).*x1([1:m])));
n=n+1;err=max(abs(x1-x2));
xvect=[xvect;x1];nvect=[nvect;n];xdif=[xdif;err];
end
脚本:
clear;
A=[3 2 1;2 3 1;1 2 3]; b=[39 34 26]; eps=10^(-5);x0=[0 0 0];w=1.2;%给定初值
[x,n,err]=SOR(A,b,eps,x0,w); %调用SOR迭代法
%下面的输出到屏幕上
fprintf(' k x1 x2 x3 err\n');
for i=1:length(n)
fprintf('%10.0f %10.6f %10.6f %10.6f %10.6f\n',n(i),x(i,1),x(i,2),x(i,3),err(i));
i=i+1;
end
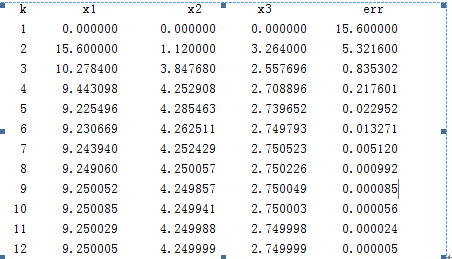
结果:
列主元消去法:
函数:
function [x,U,M]=GaussEliminate_column(A,b) %Gauss选列主元消去法
n=length(b);
M=[];
%下面是消元过程
for k=1:n
for i=k+1:n
if A(k,k)~=0
M(i,k)=A(i,k)/A(k,k);
b(i)=b(i)-M(i,k)*b(k);
for j=k+1:n
A(i,j)=A(i,j)-M(i,k)*A(k,j);
end
else
%遍历当前位置所在的列,进行消元过程
for m=k+1:n
if A(m,k)==max(A([k+1;n],k))%找到所在位置所处列以后最大的元素
%将最大元素与当前元素调换位置
B=A(k,[1:n]);
A(k,[1:n])=A(m,[1:n]);
A(m,[1:n])=B;
%将相应在b的元素也调换位置
temp=b(t);
b(t)=b(k);
b(k)=temp;
end
end
end
end
end
%下三角化零
for i=1:n
for j=1:i-1
A(i,j)=0;
end
end
U=A;
%下面是回代过程
x(n)=b(n)/A(n,n);
for i=n-1:-1:1
x(i)=(b(i)-sum(A(i,[i+1:n]).*x([i+1:n])))/(A(i,i));
end
脚本:
clear;
A=[3 2 1;2 3 1;1 2 3];b=[39 34 26];
[x,U,M]=GaussEliminate_column(A,b); %Gauss列主元消去法
%下面的输出到屏幕上
fprintf('x1= x2= x3= \n');
fprintf(' %10.5f %10.5f %10.5f \n',x(1),x(2),x(3));
fprintf('U= \n');
for i=1:length(b)
fprintf(' %10.5f %10.5f %10.5f \n',U(i,1),U(i,2),U(i,3));
end
关键代码:
%遍历当前位置所在的列,进行消元过程
for m=k+1:n
if A(m,k)==max(A([k+1;n],k))%找到所在位置所处列以后最大的元素
%将最大元素与当前元素调换位置
B=A(k,[1:n]);
A(k,[1:n])=A(m,[1:n]);
A(m,[1:n])=B;
%将相应在b的元素也调换位置
temp=b(t);
b(t)=b(k);
b(k)=temp;
end
end
结果: