HDU1710(Binary Tree Traversals)
Binary Tree Traversals
Problem Description
A binary tree is a finite set of vertices that is either empty or consists of a root r and two disjoint binary trees called the left and right subtrees. There are three most important ways in which the vertices of a binary tree can be systematically traversed or ordered. They are preorder, inorder and postorder. Let T be a binary tree with root r and subtrees T1,T2.
In a preorder traversal of the vertices of T, we visit the root r followed by visiting the vertices of T1 in preorder, then the vertices of T2 in preorder.
In an inorder traversal of the vertices of T, we visit the vertices of T1 in inorder, then the root r, followed by the vertices of T2 in inorder.
In a postorder traversal of the vertices of T, we visit the vertices of T1 in postorder, then the vertices of T2 in postorder and finally we visit r.
Now you are given the preorder sequence and inorder sequence of a certain binary tree. Try to find out its postorder sequence.
Input
The input contains several test cases. The first line of each test case contains a single integer n (1<=n<=1000), the number of vertices of the binary tree. Followed by two lines, respectively indicating the preorder sequence and inorder sequence. You can assume they are always correspond to a exclusive binary tree.
Output
For each test case print a single line specifying the corresponding postorder sequence.
Sample Input
9
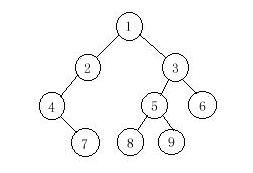
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6
Sample Output
7 4 2 8 9 5 6 3 1
题意:根据二叉树的先序序列和中序序列求后序序列
#include <iostream>
using namespace std;
const int _N = 1010;
int preorder[_N], inorder[_N], n; //定义先序,中序
/*
**算法思路: 由于先序是 头左右 中序是左头右
**则先序中的第一个必定是root,在中序中找到root,则root把中序序列分为了左子树的中序序列和右子树的中序序列
**则根据跨度,也可以在先序序列中求出左右子树的先序序列
1 2 4 7 3 5 8 9 6
4 7 2 1 8 5 9 3 6
root 1
左子树的中序遍历:4 7 2
右子树的中序遍历:8 5 9 3 6
左子树的先序遍历:2 4 7
右子树的先序遍历:3 5 8 9 6
在依次递归左子树和右子树
*/
void dfs(int pre, int in, int size, bool flag)
{
int i;
if(size <= 0)
return;
for(i = 0; preorder[pre] != inorder[in + i]; i++); //查找根出现在中序序列中的位置
dfs(pre + 1, in, i, false); //建立左子树
dfs(pre + i + 1, in + i + 1, size - i - 1, false); //遍历右子树
if(flag) //在后序中根是最后输出的
cout<<preorder[pre]<<endl;
else
cout<<preorder[pre]<<" ";
}
int main()
{
int i;
while(cin>>n)
{
for(i = 0; i < n; i++)
cin>>preorder[i];
for(i = 0; i < n; i++)
cin>>inorder[i];
dfs(0, 0, n, true);
}
return 0;
}
以下是已知中序和后序求先序
#include <iostream>
using namespace std;
const int _N = 1010;
int inorder[_N], postorder[_N], n;
void dfs(int in, int post, int size, bool flag)
{
int i;
if(size <= 0)
return;
if(flag)
cout<<postorder[post];
else
cout<<" "<<postorder[post];
for(i = 0; inorder[in + i] != postorder[post]; i++); //查找跟在中序中的位置
dfs(in, post - size + i, i, false);
dfs(in + i + 1, post - 1, size - i - 1, false);
}
int main()
{
int i;
while(cin>>n)
{
for(i = 0; i < n; i++)
cin>>inorder[i];
for(i = 0; i < n; i++)
cin>>postorder[i];
dfs(0, n - 1, n, true);
cout<<endl;
}
return 0;
}
注意:如果已知先序和后序是不能求中序的,因为先序和后序能确定root但是不能确定左右子树