图像增强——空域增强
图像增强分为空域增强和频域增强,空域增强有灰度变换增强,直方图变换增强,平滑增强,中值滤波,模板滤波和高能滤波等,下面分别讲解。
r(x,y)是输入图像,s(x,y)是输出图像
T(.)是对图像的运算
如果求某个s(x0, y0) ,只需位置(x0, y0)的像素值,则称此处理为点操作,也称灰度变换
如果需要位置(x0, y0)及其邻域的像素值,则称为模板操作
图像增强:改善图像质量,使图像更适合观察的图像处理技术
突出更多细节;对比度更合适;边缘增强;去除噪声
增强的标准带有主观性;没有完全通用的标准和技术;取决于图像希望达到的特定效果
一、灰度变换强度
当我们为了突出不同灰度的区间,或者要减弱某部分灰度,就可以使用灰度变换,下面我使用分段线性变换对灰度进行处理。
灰度线性变换
设f(x,y)是原图像的灰度值,(x,y)是变换后的灰度值,下图就是对不同区间的线性变换,灰度变换与变量x,y没有关系,这里只关系f,g函数值也就是灰度值的变换,下面就是线性变换的公式

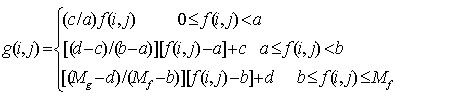
其实,可以得出曲线只要是在y=x下的就是减弱的,因为灰度比原来的减小了。
编写程序自然就很简单,根据输入参数(坐标(a,c),(b,d)),计算变换值, 建立映射表;
public int[] pixelsMap(int x1,int y1,int x2,int y2)
{
int[] pMap = new int[256]; //映射表
if(x1 > 0)
{
double k1 = y1/x1; //第1段钭率k1
//按第1段钭率k1线性变换
for(int i = 0; i <= x1; i++)
pMap[i] = (int)(k1*i);
}
double k2 = (y2-y1)/(x2-x1); //第2段钭率k2
//按第2段钭率k2线性变换
for(int i = x1+1; i <= x2; i++)
if(x2 != x1)
pMap[i] = y1 + (int)(k2*(i-x1));
else
pMap[i] = y1;
if(x2<255)
{
double k3 = (255-y2)/(255-x2);//第2段钭率k2
//按第3段钭率k3线性变换
for(int i = x2+1; i< 256; i++)
pMap[i] = y2 + (int)(k3*(i-x2));
}
return pMap;
}
根据建好的映射表就可以进行线性变换了,然后就直接输出图像public int[] stretch(int[] pix, int[] map, int iw, int ih)
{
ColorModel cm = ColorModel.getRGBdefault();
int r, g, b;
for(int i = 0; i < iw*ih; i++)
{
r = map[cm.getRed(pix[i])];
g = map[cm.getGreen(pix[i])];
b = map[cm.getBlue(pix[i])];
if(r >= 255) r = 255;
if(r < 0) r = 0;
if(g >= 255) g = 255;
if(g < 0) g = 0;
if(b >= 255) b = 255;
if(b < 0) b = 0;
pix[i] = 255 << 24|r << 16|g << 8|b;
}
return pix;
}
实验效果如下:
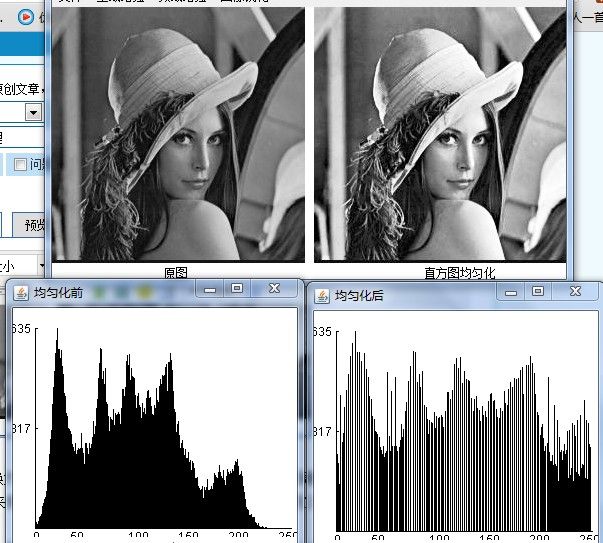
二、直方图变换增强
直方图均衡化是使原直方图变换为具有均匀密度分布的直方图,然后按该直方图调整原图像的一种图像处理技术。直方图均衡化通常用来增加许多图像的全局对比度,均衡化的标准就是以空域面积(像素总数)
这种方法对于背景和前景都太亮或者太暗的图像非常有用,这种方法尤其是可以带来X光图像中更好的骨骼结构显示以及曝光过度或者曝光不足照片中更好的细节。这种方法的一个主要优势是它是一个相当直观的技术并且是可逆操作,如果已知均衡化函数,那么就可以恢复原始的直方图,并且计算量也不大。这种方法的一个缺点是它对处理的数据不加选择,它可能会增加背景噪声的对比度并且降低有用信号的对比度。
直方图均衡操作步骤: 统计各灰度级像素数目;计算灰度概率分布;计算累积分布;折算到真实灰度值;确定灰度变换关系;进行灰度变换
映射真实灰度映射真实灰度时加上0.5,目的是能够取灰度最大值有许多疑惑
数字图像直方图均衡化的特点
• 直方图均衡化操作后,直方图有平坦的趋势,但一般不会真正平坦
• 原因:灰度的离散取值可能导致原图像多个灰度值变换到新图像的同一个灰度值上(灰度值的合并),使灰度分布与理想情况有差异。
直方图均衡化的主要思想是像素灰度值是依据灰度密度分布的,如果当前像素的灰度值>之前灰度值的平均值(平均值的以像素点数除以面积乘以255)则当前像素的灰度值将减小(这也说明小于当前像素灰度值的像素过少(稀)将当前像素降低灰度值去补充),否则将变大。
直方图均衡的优点:计算简单;无需人工干预;很多情况下效果较好
直方图均衡的不足:增强图像反差的同时增加了图像的可视粒度 (原图像的多个灰度可能变换到一个灰度上,造成灰度级减少且不连续,形成“假轮廓”);自动增强图像整体对比度,但局部效果未必最好
public int[] histequal(int[] pix, int[] hist, int iw, int ih)
{
double c = (double)255/(iw*ih);
double[] sum = new double[256];
int[] outg = new int[256];
int g, area = 256*256;
sum[0] = hist[0];
for(int i = 1; i < 256; i++)
sum[i] = sum[i-1] + hist[i];
//灰度变换:i-->outg[i]
for(int i = 0; i < 255; i++)
outg[i] = (int)(c*sum[i]);
for(int i = 0; i < iw*ih; i++)
{
g = pix[i]&0xff;
pix[i] = 255 << 24|outg[g] <<16|outg[g] << 8|outg[g];
}
return pix;
}
变换的一个目的就是:使小于当前灰度值的像素总和占图像面积(像素)的比较与变换后的灰度占255的比例是相等的,灰度的变换是根据像素比例来调整的。将原图像进行灰度变换,使变换后图像的灰度直方图呈现均匀分布
实验效果如下:
直方图变换 <!--[endif]-->灰度分布与视觉效果
初步印像:视觉效果不同的图像,直方图不同;视觉效果不好的图像的直方图比较“窄”;视觉效果好的图像的直方图比较“宽、平坦”
直观结论:若图像的像素占据全部的灰度级,且分布均匀,则图像有高对比度和丰富的细节,视觉效果比较好。即此时的灰度直方图比较均衡
若将视觉效果不好的图像(过暗/过亮/对比度低等)进行灰度变换,使其灰度直方图比较均衡,应该能改善视觉效果
只是高对比度还未必有好的效果,例如灰度在两端分布,则近似于二值图像,仍然看不清细节。
三、平衡滤波
空域滤波:利用像素本身以及邻域像素的灰度值进行图像处理的方法称为空域滤波
• 从功能上分:平滑滤波;锐化滤波
• 从算法上分:线性滤波 ;非线性滤
空域滤波时图像边缘的处理
• (1)新图像中保留原值
• (2)去除边缘部分
• (3)原图像延伸(复制,令为常数),使模板作用在边界上
平衡滤波就是依据领域像素的进行灰度处理,我们主要通过3X3的阀值滤波和3X3的均值滤波介绍平衡滤波的思想。
3X3阈值滤波,设定像素点之间灰度差值的阀值,以及超过该阀值像素的阀值来进行均衡化,查看下面程序应该是没有难度的。
public int[] threshold(int[] pix, int iw, int ih)
{
int[] opix = new int[iw*ih];
int avr, //灰度平均
sum, //灰度和
num = 0, //计数器
nT = 4, //计数器阈值
T = 10; //阈值
int pij, pkl, //(i,j),(i+k,j+l)处灰度值
err; //误差
for (int j = 1; j < ih - 1; j++)
{
for (int i = 1; i < iw - 1; i++)
{
//3X3块像素和
opix[i+j*iw] = pix[i+j*iw];
sum = 0;
for (int k = -1; k < 2; k++)
{
for (int l = -1; l < 2; l++)
{
if ((k != 0) || (l != 0))
{
pkl = pix[i+k+(j+l)*iw]&0xff;
pij = pix[i+j*iw]&0xff;
err = Math.abs(pkl - pij);
sum = sum + pkl;
if (err > T) num++;
}
}
}
int a = (int)(sum / 8.0f); //均值
if (num > nT)
opix[i + j * iw] = 255 << 24|a << 16|a << 8|a;
}
}
return opix;
实验效果如下:
//3X3均值滤波
public int[] average(int[] pix, int iw, int ih)
{
int[] opix = new int[iw*ih];
int a, pkl, sum;
for (int j = 1; j < ih - 1; j++)
{
for (int i = 1; i < iw - 1; i++)
{
opix[i+j*iw] = pix[i+j*iw];
sum = 0;
//3X3块像素和
for (int k = -1; k < 2; k++)
for (int l = -1; l < 2; l++){
pkl = pix[i+k+(j+l)*iw]&0xff;
sum = sum + pkl;
}
a = (int)(sum / 9.0f); //均值
opix[i + j * iw] = 255 << 24|a << 16|a << 8|a;
}
}
return opix;
}
四、中值滤波
中值滤波采用一个包含奇数个点的领域A(称为滑动窗口),用窗口的各点灰度中值替代窗口中心点的像素灰度值,下面看程序
//中值滤波===================================
/**************************************************
* type -- 0: 3X3窗口
* 1: 1X5窗口
* 2: 5X1窗口
* -- 3: 5X5窗口
**************************************************/
public int[] median(int[] pix, int iw, int ih, int type)
{
int[] opix = new int[iw*ih];
for (int j = 2; j < ih - 2; j++)
{
int[] dt;
for (int i = 2; i < iw - 2; i++)
{
opix[i+j*iw] = pix[i+j*iw];
int m = 0, r = 0;
if (type == 0)
{
dt = new int[9];
//3X3窗口
for (int k = -1; k < 2; k++)
{
for (int l = -1; l < 2; l++)
{
dt[m] = pix[i+k+(j+l)*iw]&0xff;
m++;
}
}
r = median_sorter(dt, 9); //返回中值
}
else if (type == 1)
{
dt = new int[5];
//1X5窗口
dt[0] = pix[i+(j-2)*iw]&0xff;
dt[1] = pix[i+(j-1)*iw]&0xff;
dt[2] = pix[i+j*iw]&0xff;
dt[3] = pix[i+(j+1)*iw]&0xff;
dt[4] = pix[i+(j+2)*iw]&0xff;
r = median_sorter(dt, 5); //中值
}
else if (type == 2)
{
dt = new int[5];
//5X1窗口
dt[0] = pix[i-2+j*iw]&0xff;
dt[1] = pix[i-1+j*iw]&0xff;
dt[2] = pix[i+j*iw]&0xff;
dt[3] = pix[i+1+j*iw]&0xff;
dt[4] = pix[i+2+j*iw]&0xff;
r = median_sorter(dt, 5); //中值
}
else if (type == 3)
{
dt = new int[25];
//5X5窗口
for (int k = -2; k < 3; k++)
{
for (int l = -2; l < 3; l++)
{
dt[m] = pix[i+k+(j+l)*iw]&0xff;
m++;
}
}
r = median_sorter(dt, 25); //中值
}
opix[i + j * iw] = 255 << 24|r << 16|r << 8|r;
}
}
return opix;
}
实验效果如下:(没意思)

五、空域模板滤波 六、高通滤波(原理太简单了,就简略讲下,其实呢,是那些公式太难打了,不愿意去找了,若有疑问,可以一起讨论)。
其实这两部分的主要原理就是使用不用比例对领域像素的灰度求平均值替代中心点像素的灰度,所谓的低通就是讲中心点的灰度值比例调高,高通自然就调低。
下面看程序:
//3X3低通滤波方法
public int[] lowpass(int[] pix, int iw, int ih, int n)
{
int[] opix = new int[iw*ih];
//定义扩展输入图像矩阵
int[][] ex_inpix = exinpix(pix, iw, ih);
int r = 0, sum;
//低通模板
int[][] h = low_matrix(n);
//低通滤波
for(int j = 1; j < ih+1; j++)
{
for(int i = 1; i < iw+1; i++)
{
//求3X3窗口9个像素加权和
sum = 0;
for(int k =- 1; k <= 1; k++)
for(int l =- 1; l <= 1; l++)
sum = sum + h[k+1][l+1]*ex_inpix[i+k][j+l];
if(n == 0)
r = (int)(sum/9); //h1平均值
else if(n == 1)
r = (int)(sum/10); //h2平均值
else if(n == 2)
r = (int)(sum/16); //h3平均值
opix[(i-1)+(j-1)*iw] = 255 << 24|r << 16|r << 8|r;
}
}
return opix;
}
//3X3高通滤波方法
public int[] highpass(int[] pix, int iw, int ih, int n)
{
int[] opix = new int[iw*ih];
//定义扩展输入图像矩阵
int[][] ex_inpix = exinpix(pix, iw, ih);
//高通模板
int[][] H = high_matrix(n);
//高通滤波
for(int j = 1; j < ih+1; j++)
{
for(int i = 1; i < iw+1; i++)
{
int r = 0, sum = 0 ;
//求3X3窗口9个像素加权和
for(int k =- 1; k <= 1; k++)
for(int l =- 1; l <= 1; l++)
sum = sum + H[k+1][l+1]*ex_inpix[i+k][j+l];
if(n == 4)
r = (int)(sum/7); //H4平均值
else if(n == 5)
r = (int)(sum/2); //H5
else
r = sum; //H1~H3
if(r > 255) r = 255;
else if( r < 0) r = 0;
opix[(i-1)+(j-1)*iw] = 255 << 24|r << 16|r << 8|r;
}
}
return opix;
}
图就不截了。
写到这里觉得空域上的变换都很简单,比较容易接受,频域要涉及一些复杂的变换看程序就比较难懂,这些东西都是我根据人家的程序写的, 当然还可以很复杂,比如变换我可以不是线性变换的,可以根据需求做任意的变换,掌握原理了都比较好办,之前一直被那些名词(滤波,阀值等)吓到了,一直没有入手数字图像处理,现在觉得还是可以学习的,接下来就要学习频域的滤波,希望能顺利完成。