Trie三兄弟——标准Trie、压缩Trie、后缀Trie
Trie三兄弟——标准Trie、压缩Trie、后缀Trie
1.Trie导引
Trie树是一种基于树的数据结构,又称单词查找树、前缀树,是一种哈希树的变种。应用于字符串的统计与排序,经常被搜索引擎系统用于文本词频统计。用于存储字符串以便支持快速模式匹配,主要应用在信息检索中,Trie支持的主要查询操作是模式匹配和前缀匹配。Trie树可以看着是一个确定有限状态自动机,有限状态自动机另一篇博文字符串模式匹配算法——BM、Horspool、Sunday、KMP、KR、AC算法一网打尽 有介绍。
2.标准Trie
令S是取自字母表∑的s个集合,满足S中不存在一个串是另一个串的前缀。S的一个标准Trie(standard trie)是一颗有序书T,满足如下性质:
- 除了根之外,T中的每个结点标记有∑的一个字符。
- T中一个内部结点的子结点的次序有字母表∑上的规范次序确定。
- T有s个外部结点(叶结点),每个外部结点关联S中的一个串,满足从根到T中一个外部结点v的路径上标记连接产生S中关联的一个串。
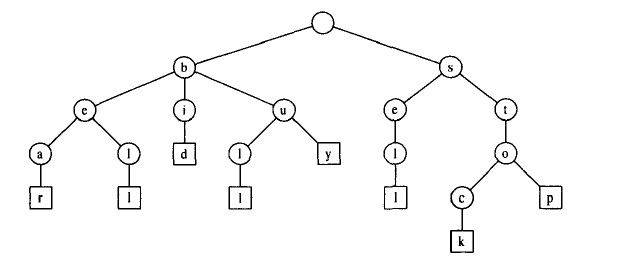
下图是串{bear,bell,bid,bull,buy,sell,stock,stop}的标准Trie
存储总长为n,来自大小为d的字母表中s个串的集合S的标准Trie具有如下性质:
- T中每个内部结点最多有d个子结点。
- T有s个外部结点。
- T的高度等于最长串的长度。
- T中的结点书为O(n)。
性能:对于有n个英文字母的串来说,在内部结点中定位指针所需要花费O(d)时间,d为字母表的大小,英文为26。由于在上面的算法中内部结点指针定位使用了数组随机存储方式,因此时间复杂度降为了O(1)。但是如果是中文字,下面在实际应用中会提到。因此我们在这里还是用O(d)。 查找成功的时候恰好走了一条从根结点到叶子结点的路径。因此时间复杂度为O(d*n)。但是,当查找集合X中所有字符串两两都不共享前缀时,trie中出现最坏情况。除根之外,所有内部结点都自由一个子结点。此时的查找时间复杂度蜕化为O(d*(n^2))
中文词语的标准Trie树
由于中文的字远比英文的26个字母多的多。因此对于trie树的内部结点,不可能用一个26的数组来存储指针。如果每个结点都开辟几万个中国字的指针空间。估计内存要爆了,就连磁盘也消耗很大。
一般我们采取这样种措施:
(1) 以词语中相同的第一个字为根组成一棵树。这样的话,一个中文词汇的集合就可以构成一片Trie森林。这篇森林都存储在磁盘上。森林的root中的字和root所在磁盘的位置都记录在一张以Unicode码值排序的有序字表中。字表可以存放在内存里。
(2) 内部结点的指针用可变长数组存储。
特点:由于中文词语很少操作4个字的,因此Trie树的高度不长。查找的时间主要耗费在内部结点指针的查找。因此将这项指向字的指针按照字的Unicode码值排序,然后加载进内存以后通过二分查找能够提高效率。
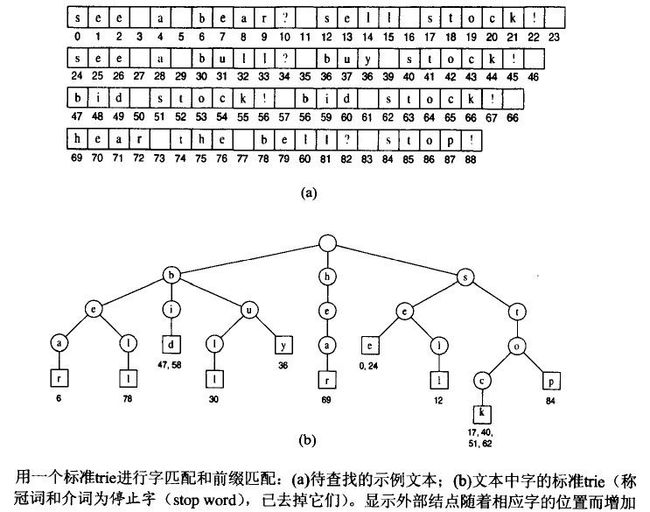
标准Trie的应用举例
标准Trie的应用和优缺点
(1) 全字匹配:确定待查字串是否与集合的一个单词完全匹配。
(2) 前缀匹配:查找集合中与以s为前缀的所有串。
注意:Trie树的结构并不适合用来查找子串。这一点和前面提到的PAT Tree以及后面专门要提到的Suffix Tree的作用有很大不同。
优点: 查找效率比与集合中的每一个字符串做匹配的效率要高很多。在o(m)时间内搜索一个长度为m的字符串s是否在字典里。
缺点:标准Trie的空间利用率不高,可能存在大量结点中只有一个子结点,这样的结点绝对是一种浪费。正是这个原因,才迅速推动了下面所讲的压缩trie的开发。
压缩Trie
压缩Trie类似于标准Trie,但它能保证Trie中的每个内部结点至少有两个字结点。通过把单子结点链压缩进各条边中来执行这个规则。设T是一棵标准Trie,如果T的一个内部结点v有一个子结点且它不是根,则称为这个内部结点是内部结点是冗余的(redundant)。
如果
串{bear,bell,bid,bull,buy,sell,stock,stop}的压缩Trie
压缩Trie的性质和优势:
与标准Trie比较,压缩Trie的结点数与串的个数成正比了,而不是与串的总长度成正比。一棵存储来自大小为d的字母表中的s个串的结合T的压缩trie具有如下性质:
(1) T中的每个内部结点至少有两个子结点,至多有d个子结点。
(2) T有s个外部结点。
(3) T中的结点数为O(s)
存储空间从标准Trie的O(n)降低到压缩后的O(s),其中n为集合T中总字符串长度,s为T中的字符串个数。
压缩Trie应用举例
假定串的集合S是S[0],S[1],...,S[s-1]的一个数组,使用三元组(i,j,k)隐式地表示存储的标记X,满足X=S[i][j,...,k];即X是S[i]的子串,由从j到k所包含的字符组成。
后缀Trie
后缀Trie的字符串集合是由指定字符串的后缀子串构成的。比如、完整字符串"minimize"的后缀子串组成的集合S分别如下:
s1=minimize
s2=inimize
s3=nimize
s4=imize
s5=mize
s6=ize
s7=ze
s8=e
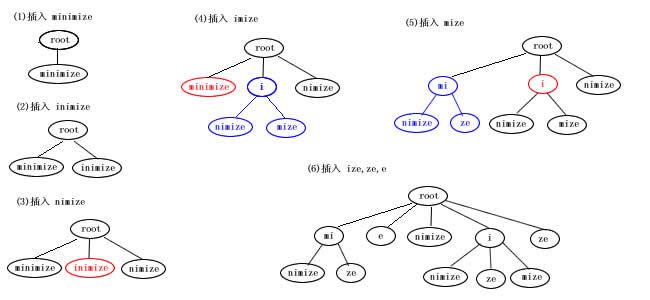
然后把这些子串的公共前缀作为内部结点构成一棵"minimize"的后缀树,如下图所示:
节省空间
因为长度为n的串X的后缀总长度为n(n+1)/2,显式存储X的所有后缀所需空间为O(n²)。而后缀Trie隐式地表示这些串所需空间为O(n)。
后缀Trie创建(图示)
当插入子串时,发现叶子结点中的关键字与子串有公共前缀,则需要将该叶子结点分裂。如上图第3到4步。否则,重新创建一个叶子结点来存放后缀,如上图第1到2步。
Suffix Trie的子串查询
如果在后缀树T中查找子串P,我们需要这样的过程:
(1) 从根结点root出发,遍历所有的根的孩子结点:N1,N2,N3....
(2) 如果所有孩子结点中的关键字的第一个字符都和P的第一个字符不匹配,则没有这个子串,查找结束。
(3) 假如N3结点的关键字K3第一个字符与P的相同,则匹配K3和P。
若 K3.length>=P.length 并且K3.subString(0,P.length-1)=P,则匹配成功,否则匹配失败。
若 K3.length<=P.length 并且K3=P.subString(0, K3.length-1),则将子串P1=P.subString(K3.length, P.length); 即取出P中排除K3之后的子串。然后P1以N3为根结点继续重复(1)~ (3)的步骤。直到匹配完P1的所有字符,则匹配成功。否则匹配失败。
查询效率:很显然,在上面的算法中。匹配成功正好比较了P.length次字符。而定位结点的孩子指针,和Trie情况类似,假如字母表数量为d。则查询效率为O(d*m),实际上,d是固定常数,如果使用Hash表直接定位,则d=1.
因此,后缀树查询子串P的时间复杂度为O(m),其中m为P的长度。但是构造后缀Trie的时间为O(dn)。
后缀Trie应用
标准Trie树只适合前缀匹配和全字匹配,并不适合后缀和子串匹配。而后缀Trie在这方面则非常合适。
参考:
①Michael T. Goodrich Roberto Tamassia Algorithm Design Foundations, Analysis, and Internet Examples
②Heart.X.Raid: http://hxraid.iteye.com/blog/618962
③Heart.X.Raid: http://hxraid.iteye.com/blog/620414